2. Застосування критерія.

Покажемо застосування критерію Гурвіца для декількох часткових випадків. Для характеристичного рівняння першого порядку

а₁р + а₀ = 0. (5.3)

Умова стійкості

Δ₁ = а₀>0. (5.4)

Таким чином, при а₁>0 критерій зводиться до вимог позитивності обох коефіцієнтів. Цей результат наявний, так як тільки при цих умовах єдиний корінь характеристичного рівняння буде негативним. Для характеристичного рівняння другого порядку:

а₂р² + а₁р + а₀ = 0, (5. 5)

a0	0
a1	a2

маємо: Δ₂ = · Δ₁.

Тоді умова стійкості має такий вигляд:

а₂>0, |Δ₁ |=а₁>0, Δ₂ = а₀ а₁ >0. (5. 6)

Для характеристичного рівняння третього порядку:

а₃р³ + а₂р² + а₁р + а₀ >0. (5. 7)

Матриці Гурвіца

a0	0	0
a2	a1	a0
0	a3	a2

Δ₃ = = а₀ ( а₁а₂ – а₀ а₃),

Умови стійкості складаються в виконанні нерівностей

а₁ а₂ - а₀ а₃ >0; (5. 8)

а₃>0; а₂>0; а₁>0; а₀>0.

Звідки виходить, що для того, щоб автоматична система третього порядку була стійкою, необхідно та достатньо, щоб усі коефіцієнти її характеристичного рівняння були б позитивними, а добуток середніх коефіцієнтів був більше добутку крайніх коефіцієнтів.

3. Дослідження стійкості CAP.

За заданою структурною схемою CAP (рис. 9) за допомогою критерію Гауса - Гурвіца визначити її стійкість, якщо коефіцієнт К= 80С^-2

Х(Р)

У(Р)

Рис. 9

5.3.1. Визначення передавальної функції CAP.

Визначимо передавальну функцію CAP. З малюнку 9 видно, що структурна схема охоплена від’ємним зворотнім зв'язком, тому передавальна функція системи може бути записана у вигляді:

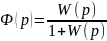(5. 9)

Підставимо в (5. 9) задане значення структурної схеми

5.3.2. Визначення характеристичного рівняння

Запишемо характеристичне рівняння:

а(р) = р²(0,1р + 1)(0,05р +1) + К(0,5р +1) = 0,005р⁴ + 0,15р³ + р² + 0,5 Кр + К.

Позначимо коефіцієнти характеристичного рівняння:

а₄= 0,005;

а₃=0,15;

а₂ = 1;

а₁ =0,5 · 80=40;

а₍₎ =80.

3. Дослідження стійкості CAP.

Дослідимо стійкість системи. Для цього складемо матрицю Гурвіца

а()	0	0	0
а2	а1	а()	0
а4	а3	а2	а1
0	0	а4	а3

80	0	0	0
1	40	80	0
0,005	0,15	1	40
0	0	0,005	0,15

Δ₄ = =

Перевіряємо позитивність Δ_і

Δ₁ = а3 = 0,15 >0;

a2	0
a3	a4

Δ₂ = = a₂а₃ - a₁a₄ =1•0,15-40 · 0,005 = - 0,05

a1	a0	0
a3	a2	a1
0	a4	a3

Δ₃ = =a₁ a₂ a₃ – a₀ a₃² – a₁² a₄ = 40 •1• 0,15 - 80•0,15² –40•0,005=4

З аналізу отриманих результатів робимо висновок, що необхідні умови стійкості виконані.

Достатні умови стійкості не виконані, так як Δ₂ від’ємний, таким чином CAP не стійка.