2. Matlab.
Лекция 8 (13).
2.9. Символьные вычисления в Matlab.
В состав MATLAB входит Symbolic Math Toolbox, предназначенный для вычислений в символьном виде. Этот Toolbox позволяет выполнять: преобразование выражений, аналитическое решения задач линейной алгебры, дифференциальное и интегральное исчисления, получение численного результата с любой точностью и многое другое.
2.9.1. Символьные переменные и функции [1, с. 751].
Объектно-ориентированный подход, реализованный в MATLAB, позволил сделать работу с символьными выражениями простой и удобной. Символьные переменные и функции являются объектами класса sym object, в отличие от числовых переменных, которые содержатся в массивах double array. Символьный объект создается при помощи функции syms. Пример команды, создающей три символьные переменные :
» syms х а b
Размер памяти, отводимый по умолчанию под символьные переменные, достаточно большой. Если посмотреть данные по определенным таким образом переменным в окне Workspace браузера рабочей среды или вызвать команду whos, то можно увидеть следующую информацию:
» whos x a b
Name Size Bytes Class
а lxl 126 sym object
b lxl 126 sym object
х lxl 126 sym object
Grand total is 6 elements using 378 bytes
Конструирование символьных функций, зависящих от переменных класса sym object, производится с использованием обычных арифметических операций и обозначений для встроенных математических функций, например:
» f = (sin(x) + а)^2*(cos(x) + b)^2/sqrt(abs(a + b))
f =
(sin(x) + а)^2*(cos(x) + b)^2/abs(a + b)^(1/2)
Запись формулы для выражения в одну строку не всегда удобна, более естественный вид выражения выводит в командное окно функция pretty:
» pretty(f)
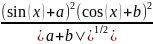
Определенная функция f также является символьной переменной типа sym object, что можно увидеть при помощи браузера переменных.
Символьные переменные и функции могут создавать новые символьные выражения:
» syms у
» g = (ехр(-у) + 1)/ехр(у) % переменная g стала символьной
g =
(ехр(-у) + 1)/ехр(у)
» h = f*g
h =
(sin(x) + а)^2*(cos(x) + b)^2/abs(a + b)^(1/2)*(exp(-y) + l)/exp(y)
» pretty(h)
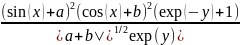
Без предварительного объявления переменных символьную функцию можно создать при помощи функции sym, входным аргументом которой является строка с выражением, заключенная в апострофы:
» z = sym('c^2/(d + 1)')
z =
c^2/(d + 1)
» pretty(z)
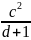
Команда syms a, b, с эквивалентна последовательности а = sym('a'); b = sym('b'); c = sym('c').
При работе в области комплексных чисел следует указать, что определяемые переменные являются, в общем случае, комплексными. Комплексные символьные переменные задаются командой syms с опцией unreal. Опция real означает, что переменные интерпретируются как вещественные. Результат символьных вычислений зависит от того, какие символьные переменные используются — вещественные или комплексные. Примеры (проверки записей):
» syms a b real
» р = conj(a + i*b)
p =
а - i*b
» syms a b unreal % здесь a и b - комплексные
» q = conj(a + i*b)
q =
conj(a + i*b)
В последнем случае знак комплексно сопряженного числа остался тот же самый.
Использование одних и тех же операторов в символьных и числовых выражениях возможно благодаря тому, что пакет MATLAB является объектно- ориентированной системой. Для сложения чисел и числовых массивов в MATLAB зарезервирован знак +, который приводит к вызову встроенной функции plus, расположенной в подкаталоге \toolbox\matlab\ops\ основного каталога MATLAB. Можно проверить, что 1.3 + 2.9 и plus (1.3, 2.9) приводят к одинаковому результату. Для символьных переменных и функций используется файл-функция с тем же именем plus, находящаяся в подкаталоге \toolbox\symboIic\@sym\ основного каталога MATLAB. Если открыть из последней папки файл plus.m в редакторе MATLAB (для того, чтобы посмотреть, как решаются вопросы по использованию разных классов объектов; но не вносить в него изменений!!!), то можно увидеть, что сначала оба ее входных аргумента приводятся к символьному типу данных при помощи функции sym. Это позволяет складывать символьную переменную с числовой и получить символьный результат. Далее проверяется совпадение размеров входных аргументов, которые могут быть массивами. Последняя строка содержит вызов функции maple, служащей для обращения к соответствующей функции или оператору из ядра пакета Maple — в данном случае символьному сложению (MATLAB использует библиотеку функций, являющихся вычислительным ядром системы Maple).
Говоря на языке объектно-ориентированного программирования, числовые переменные типа double array образуют класс со своими методами (в том числе plus). Для класса символьных объектов sym метод plus переопределен. MATLAB определяет по типу аргумента соответствующий метод класса и выполняет его.
Пользователь MATLAB может создавать собственные классы и определять их методы, в том числе и переопределять методы предка класса. Выполнение подобных действий требует понимания основ объектно-ориентированного программирования. Создание классов в MATLAB описано в справочной системе MATLAB в разделе “Classes and Objects”.