2. Matlab.
Лекция 7 (12).
2.8. Решение уравнений в Matlab.
2.8.1. Решение систем линейных уравнений [3, с.35, 125].
Традиционный для операции деления знак / (а также знак \) закреплен в системе MATLAB за решением довольно сложной задачи линейной алгебры -нахождением корней систем линейных уравнений. Например, если требуется решить систему линейных уравнений
AY = B ,
где А - заданная квадратная матрица размера N х N, B - заданный вектор-столбец длины N, то для нахождения неизвестного вектор-столбца Y (неизвестны его элементы) достаточно вычислить выражение A\B. Пример:
А = [1, -2, 3, -1; 2, 3, -4, 4; 3, 1, -2, -2; 1, -3, 7, 6];
B = [6; -7; 9; -7];
Y = A \ B
Y =
2.0000
-1.0000
0
-2.0000
В общем случае операция \ называется левым делением матриц и, будучи примененная к матрицам А и В в виде А\В, примерно эквивалентна вычислению выражения
inv(A)*B ,
но при этом вычисляется по-другому. Здесь под inv (А) понимается вычисление матрицы, обратной к матрице А.
Операцию / называют правым делением матриц. Выражение А/В примерно соответствует вычислению выражения B*inv(A). Значит, эта операция позволяет решать системы линейных уравнений вида YA = В ,
так как решением именно этого уравнения служит выражение B*inv (A).
Считывание из внешних файлов и запись данных при решении систем линейных уравнений см. [1, с.86].
2.8.2. Поиск не комплексных корней уравнений (нахождение нулей функций) [1, с. 246; 3, с. 133].
Любое уравнение можно записать в виде равенства некоторой функции нулю, так что это и есть задача о нахождении нулей функций.
Решение указанной задачи осуществляет функция fzero. В качестве первого аргумента ей передается имя функции, задающей исходное уравнение (текстовый аргумент). Вторым аргументом служит начальное приближение к корню. Например, для решения уравнения cos(x) = 0 можно записать:
х = fzero ( 'cos', 1 )
x =
1.5708
Эта величина приближенно соответствует точному значению корня, равному pi/2.
Если требуется найти корень выражения, отличающегося от встроенной в систему MATLAB функции, то нужно приписать некоторое имя выражению, вычисляющему функцию (т.е. создать М-функцию).
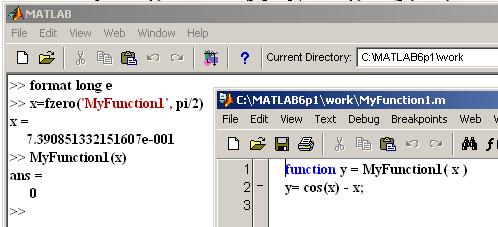
Пусть, например, требуется найти корни уравнения cos(х) = х, что эквивалентно нахождению нулей функции, вычисляемой по формуле у = cos(х) - х, не имеющей в рамках системы фиксированного имени. В этом случае нужно в текстовом редакторе MATLAB ( или в любом другом простейшем текстовом редакторе) набрать две строки следующего кода:
function у = MyFunction1( х )
у = cos(x) - х;
и запомнить их в файле MyFunction1 .m, который нужно разместить в текущем каталоге системы MATLAB (узнать его можно командой cd; желательно сохранять в папке “Work”). После этого можно воспользоваться функцией fzero:
х = fzero('MyFunction1', pi/2)
x =
0.7391 .
Можно вызвать функцию MyFunction1 в командной строке MATLAB для вычисления значения функции при найденном значении корня:
Функция fzero находит нули только вещественнозначных функций одной вещественной переменной. Однако часто бывает необходимо найти комплексные корни вещественнозначных функций, особенно в случае многочленов. Для этого в MATLAB существует специальная функция roots, которая будет рассмотрена в следующем разделе (2.8.3.).
Перед нахождением корней с помощью функции fzero полезно построить график выражения, входящего в левую часть уравнения. Для получения графика можно использовать функцию plot, но если уравнение задано в М - файле, то имеет смысл воспользоваться функцией fplot, которая позволяет получить более точный график по сравнению с plot.
Например, если есть М-функция следующего содержания:
function у = myf(x)
у = sin(x) – х .^2 .* cos(x);
то график, построенный с помощью функции fplot, имеет вид:
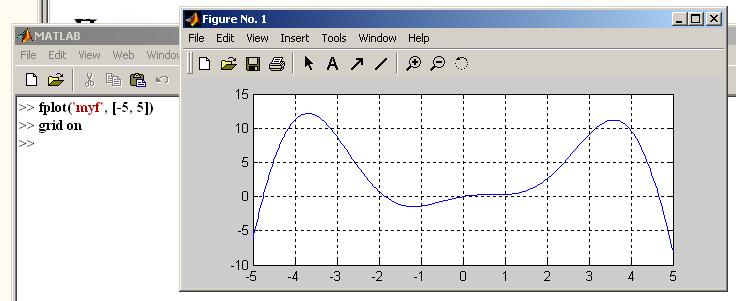
По графику видно, что уравнение имеет 4 решения. Задавая соответствующие начальные значения можно раздельно определить с помощью функции fzero все корни. Точность полученных результатов можно определить с помощью функции eps. На компьютере вычисления производятся с числами, имеющими 52 двоичных разряда в мантиссе (без учета порядка числа). Это соответствует относительной погрешности представления чисел, которую возвращает функция eps, вызываемая без входных аргументов:
» eps
ans =
2.220446049250313е-016
Алгоритм функции f zero по умолчанию находит корень уравнения с точностью eps, т. е. 2 в шестнадцатом знаке после десятичной точки — практически с максимально возможной точностью. Самое точное представление числа в десятичной форме для пакета MATLAB выполняется в формате format long е. В предыдущем абзаце значение функции eps выведено в этом формате.
Можно убедиться, с какой точностью выполнен расчет, вычислив уравнение дважды: для найденного значения корня и для измененной его величины на единицу в последнем знаке десятичного числа после запятой. Если значения функции будут иметь разные знаки, следовательно, ошибка будет в последней значащей цифре (учесть, что может потребоваться единицу в последней цифре не добавлять, а - вычитать). Например, функции myf меняет знак значения функции с минуса на плюс при подстановке величины второго корня (соответствующего значению ~ -2 на рисунке выше), измененной на 1 в пятнадцатом знаке после запятой в значении корня:
