2.7.3. Пример ргз.

Пример расчета суммы членов разложения в ряд функции sin(x) и расчета выражения sin(x)/(1+x) для 5 значений х с точностью 0.001. Программа выводит график указанного выражения в рассчитываемом диапазоне изменения переменной x. Кроме того, приводятся строки результатов расчета для каждого значения х : число суммируемых членов разложения (n); значение выражения, рассчитанное с использованием суммы членов разложения; значение выражения с применением (для сравнения) внутренней тригонометрической MATLAB - функции sin(x); значение переменной х.

Текст программы:

Результаты расчета:

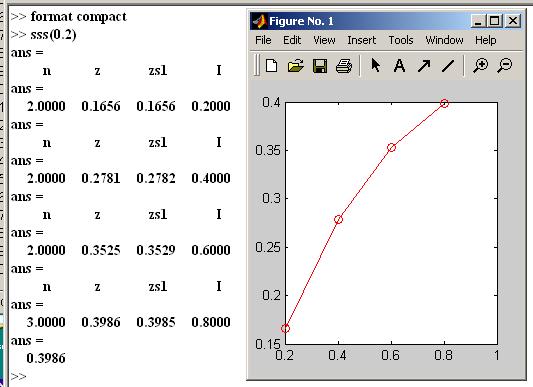
Файл записывается в текстовый редактор MATLAB, который можно вызвать из меню: File – New – Blank M-File или функцией edit из командной строки или одновременным нажатием клавишей Ctrl-N.

2.7.4. Пример м-файла: метод половинного деления.

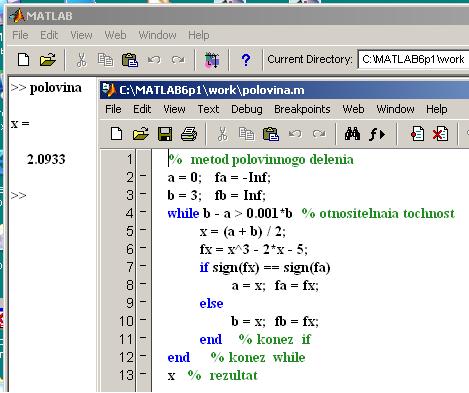
-текущая директория М-файлов “по умолчанию” –work.

- решается уравнение

x³ -2х – 5 =0.

Текст этой же программы, составленной по алгоритму, используемому в лабораторной работе по MathCAD (раздел 1.9.4.), приведен на рисунке ниже. Рядом с этим рисунком справа приведен рисунок с фрагментами записей в командной строке MATLAB, иллюстрирующими расчет корней полинома с помощью функции roots и с результатами подстановки значений корней в уравнение fx = x3 -2x -5 . Функция roots позволяет не только быстро найти корни полинома, но и определить их, если они еще и комплексные:

2.7.5. М-функции с переменным числом входных параметров и выходных значений [4].

Бывают ситуации, когда полезно иметь одну функцию, которая штатно обрабатывала бы переменное число входных параметров и выходных значений. Например, неплохо иметь функцию, которая может суммировать элементы произвольного числа векторов. Такая функция должна уметь распознавать реальное количество параметров, с которыми она вызвана.

В М-языке системы MATLAB такая возможность базируется на использовании массива ячеек. В таких массивах элементы являются ячейками и могут служить «хранилищами» для других массивов данных. Например, одна ячейка массива ячеек может содержать матрицу действительных чисел, другая ячейка – массив текстовых строк, а третья – вектор комплексных значений. Фигурные скобки, “{}”, являются такими же “конструкторами” массивов ячеек, как квадратные скобки являются “конструкторами” числовых массивов. Фигурные скобки используются совершенно аналогично квадратным скобкам, за тем исключением, что их можно использовать для вложения массивов ячеек.

При конструировании массивов с использованием фигурных скобок нужно использовать пробелы или запятые для разделения столбцов, и точки с запятой для разделения строк. Например, ввод C = {[1 2], [3 4]; [5 6], [7 8]};

приводит к созданию массива ячеек размером 2х2.

Используется 2 допустимых формы записи элементов массивов ячеек с помощью индексов [1, с. 86]. Первая форма:

A(1,1) = {[1 4 3; 0 5 8; 7 2 9]};

A(1,2) = {'Anne Smith'};

A(2,1) = {3+7i};

A(2,2) = {–pi:pi/10:pi};

Вторая форма: A{1,1} = [1 4 3; 0 5 8; 7 2 9];

A{1,2} = 'Anne Smith';

A{2,1} = 3+7i;

A{2,2} = –pi:pi/10:pi;

В определении М-функции параметр, через который передается заранее неизвестное число входных аргументов, нужно обозначить ключевым словом varargin. Таким ключевым словом обозначается массив ячеек, в который упакованы эти параметры. Всегда можно узнать истинное число аргументов, упакованных в параметре varargin, применив для этого функцию length.

Ниже представлен код функции, вычисляющей сумму квадратов элементов произвольного количества вектор-строк:

function SumLen = NumLength() %имя varargin только в описании -

n = length( varargin ); SumLen = 0; % формальный параметр

for k = 1 : n

SumLen = SumLen+varargin{k}(1)^2+varargin{k}(2)^2;

end

Если аргумент varargin не единственный в списке параметров, то он должен стоять последним. В рассмотренном примере с помощью фигурных скобок извлекается содержимое отдельной ячейки массива, а с помощью дальнейшей индексации круглыми скобками извлекаются первый и второй элемент (координаты) вектора (в примере принято, что вектор в каждой ячейке имеет 2 элемента; см. ниже пример).

При вызове функции NumLength не нужно (и нельзя) упаковывать входные числовые вектор-строки в массив ячеек (т. е. ставить фигурные скобки), так как MATLAB делает это сам. Достаточно перечислить их в качестве фактических параметров через запятую:

NumLength( [1 2], [3 4] )

ans =

30

Если увеличить число элементов в векторах, то результат не изменится, т.к. в функции NumLength в цикле используются только два элемента векторов, являющихся составными частями массива ячеек:

NumLength( [1 2 3], [3 4 5] )

ans =

30

Пример вызова функции NumLength с другим числом аргументов:

NumLength( [1 2], [3 4], [5 6] )

ans =

91

Функция NumLength легко обрабатывает эти примеры, правильно вычисляя суммарное значение величин, рассчитанных по каждому вектору.

В определении М-функции переменное число возвращаемых значений (выходных параметров) упаковывается в массив ячеек, обозначаемый ключевым словом varargout:

function varargout = MyFunc3( X )

Здесь в массив ячеек с именем varargout можно в теле функции упаковать произвольное число выходных значений. Допустим, что на вход функции MyFunc3 может подаваться в качестве единственного входного параметра массив разных размерностей и размеров. Требуется возвращать несколько скаляров, каждый из которых имеет такой же размер, как входной массив вдоль одного из его измерений. Так как количество измерений заранее неизвестно, то его можно определить в теле функции динамически и на ходу упаковать все эти скаляры в единственную выходную переменную varargout. Вот решение этой задачи:

function varargout = MyFunc3( X )

n = ndims( X ); % определение размера для создания выходного массива с таким

for i = 1 : n % же размером

varargout(i) = {size(X,i)};

end

Здесь функция size (X, i) при i=1 вычисляет число строк массива Х (т.е. размер по первому измерению); при i=2 - число столбцов массива Х (т.е. размер по второму измерению); при i=3 - число по 3-му измерению массива Х и т. д.

Ниже показаны два примера использования этой функции; первый пример:

А=[4 5 6; 7 8 9];

[ m, n ] = MyFunc3 ( А );

Здесь скаляры m и n примут соответственно значения 2 и 3. Второй пример – создание трехмерного массива С и вызов для него функции MyFunc3:

В = [ 6 5 4; 9 8 7];

С(:, :, 1) = А; С(:, :, 2) = В; [m,n,k]= MyFunc3( С );

Скаляры m, n и k примут значения 2, 3, 2. В них помещены размеры трехмерного массива С вдоль всех его измерений. Если бы требовались размеры этого массива вдоль только первых двух измерений, то можно было бы вызвать функцию MyFunc3 в следующем формате:

[m,n]= MyFunc3( С );

Такая запись является абсолютно корректной с точки зрения синтаксиса М-языка, но при этом третье вырабатываемое функцией MyFunc3 выходное значение теряется.

Литература.

1. Гаспарян О.Н. MATLAB: Учебное пособие. - Баку: ГИУ Армении, 2005. 143 с. (PDF формат)

2. Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н. MATLAB 7. Наиболее полное руководство.- СПб.: БХВ-Петербург, 2005. - 1104 с: ил.

Matlab7NaiboleePolnoeRukovodstvo.djvu, глава5, с. 212.

3. Иллюстрированный самоучитель по MatLab 6 (23 урока). Урок 5.

http://www.radiomaster.ru/cad/matlab/glava5/index1.php

4. Н.Н.Мартынов, А.П.Иванов. MATLAB 5.x. Вычисления, визуализация, программирование.- М.: КУДИЦ-ОБРАЗ, 2002.-336с.

Оглавление

2. MATLAB. 1

2.7. Программирование на языке Matlab. 1

2.7.1. После вызова М-файла MATLAB выполняет следующие действия: 4

2.7.2.Подфункции. 5

2.7.3. Пример РГЗ. 5

2.7.4. Пример М-файла: метод половинного деления. 7

2.7.5. М-функции с переменным числом входных параметров и выходных значений [4]. 8