Свойства треугольников на плоскости Лобачевского

Теорема 3. Сумма углов треугольника в геометрии Лобачевского есть величина постоянная и зависит от формы и размеров треугольника.

Теорема 4. На плоскости Лобачевского не существует подобных треугольников.

Теорема 5. На плоскости Лобачевского не около всякого треугольника можно описать окружность.

Доказательство. В геометрии Евклида около любого треугольника можно описать окружность, центр которой есть точка пересечения серединных перпендикуляров к сторонам треугольника. Существование такой точки пересечения доказывается на основе постулата Евклида. Итак, это утверждение эквивалентно постулату.

Правда, пусть имеем треугольник , в котором - середины сторон соответственно (рис. 32).

Проведем через точки перпендикуляры . Тогда угол - острый (из ), а угол - прямой, потому сумма и по постулату прямые пересекаются в точке О, которая есть центр описанной окружности.

На плоскости Лобачевского существование точки О пересечения серединных перпендикуляров зависит сторон зависит от величины угла , который есть функция отрезка , а сама функция Лобачевского: прямые параллельны, а при расходятся (рис. 32). Теорема доказана.

Понятие про эквидистанту

Пусть на плоскости имеется какая-нибудь прямая и на ней несколько точек Проведем через эти точки прямые, перпендикулярные к прямой , отложим на них отрезки от прямой (рис. 33).

Соединим точки гладкой линией, получим некоторую линию, все точки которой равноудалены от прямой .

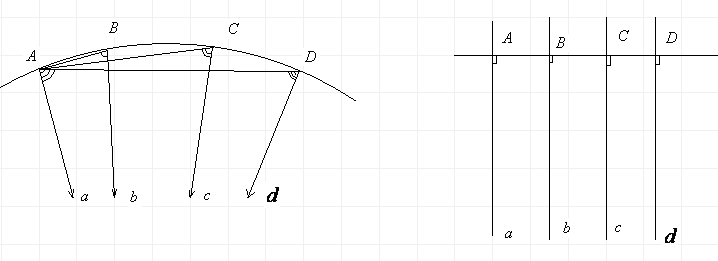
Определение. Геометрическое место точек плоскости, расположенных по одну сторону от прямой , на одинаковом расстоянии от нее, называется эквидистантою. Обозначают е.

Эквидистанта на плоскости Лобачевского – это выпуклая кривая линия.

Основные свойства эквидистанты

1.Эквидистанта может двигаться сама по себе, не деформируясь.

2.Каждая прямая с эквидистантою может иметь не больше двух общих точек.

3.Эквидистанта на плоскости Лобачевского – выпуклая кривая, выпуклостью направленная в сторону от базы а.

4.Касательная к эквидистанте перпендикулярна к высоте, проведенной через точку касания (рис.34).

5.Все точки эквидистанты расположены по одну сторону от касательной, проведенной через произвольную ее точку А, в сторону базы а.

Понятие про орицикл

Введем сначала понятие секущей равного наклона двух прямых.

Определение. Прямая называется секущей равного наклона к прямым , если она образует с ними по одну сторону равные внутренние углы.

Можно доказать, что через каждую точку одной из двух данных прямых всегда можно провести только одну секущую равного наклона этих прямых.

Возьмем пучок прямых . На одной из них, пусть на прямой , возьмем произвольную точку и через нее проведем секущую равного наклона прямой и каждой другой прямой пучка: .

На евклидовой плоскости точки лежат на одной прямой, перпендикулярной к прямой пучка (рис. 35). Это вытекает из V постулата Евклида.

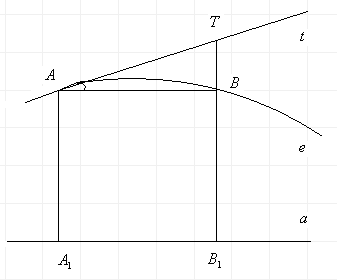
На плоскости Лобачевского орицикл – выгнутая кривая линия.

Определение. Геометрическое место точек пересечения прямых параллельного пучка с секущими равного наклона, проведенных из произвольной точки одной из них к каждой другой прямой пучка, называется орициклом или граничной линией пучка.

Прямые пучка называются осями орицикла, точки вершинами орицикла, отрезки - ее хордами.

Основные свойства орицикла

1.Каждый орицикл полностью определяется заданием одной его осью и одной его точкой.

2.Какая-либо прямая с орициклом может иметь не больше двух общих точек.

3.Точка пересечения прямой , проведенной через середину хорды орицикла перпендикулярно к этой хорде, с орициклом есть вершина орицикла.

4.Все внутренние точки хорды орицикла лежат в середине орицикла, а все внешние точки хорды лежат вне орицикла.

5.Орицикл – выгнутая кривая линия, выпуклостью направленную в сторону, противоположную направлению параллельности.

6.Орицикл не зависит от того, какую из точек взять за первую.

7.Один и тот же пучок параллельных прямых определяет бесконечно много орициклов, причем равных между собой.

8.Каковы бы ни были две точки А и В плоскости, через них можно провести точно два орицикла, симметричных относительно прямой АВ.

9.Все точки орицикла лежат по одну сторону от перпендикуляра, проведенного в какой-либо вершине к оси, а точнее в сторону параллельности осей. Итак, каждая ось орицикла есть нормалью.

10.Орицикл можно рассматривать как предельное положение окружности с бесконечно удаленным центром.