Геометрия Лобачевского; ее модели

Совокупность всех утверждений, которые можно доказать без использования аксиомы параллельности, или эквивалентных ей утверждений, называются абсолютной геометрией.

К абсолютной геометрии принадлежат, например, три признака равенства треугольника, теоремы про внешний угол треугольника, про равность прямых углов, про равность вертикальных углов, про то, что сумма смежных углов равна , сумма двух сторон треугольника больше третьей, перпендикуляр короче наклонной, гипотенуза треугольника больше катета, про то, что две прямые, перпендикулярные третьей, не пересекаются, что сумма углов треугольника не превышает и. д.

Геометрия Лобачевского строится на тех же аксиомах, что и геометрия Евклида, с единственной заменой аксиомы параллельности на противоположную.

Аксиома Лобачевского. На плоскости для каждой прямой а через каждую не лежащую на ней точку проходит, по крайней мере, две прямые, не пересекающие данную прямую.

Факты геометрии Лобачевского

Здесь мы укажем ряд фактов геометрии Лобачевского, которыми она отличается от геометрии Евклида, прежде всего на плоскости.

Параллельные прямые на плоскости Лобачевского

Из аксиомы Лобачевского сразу выходит, что через точку, взятую вне данной прямой, можно провести бесконечно много прямых, которые ее не пересекают. На самом деле, пусть через точку М проходит две прямые , которые не пересекают прямую а, их существования обеспечивается аксиомой Лобачевского (рис.23).

Тогда, очевидно, все прямые, которые проходят в середине вертикальных углов , не пересекают а (если бы какая-нибудь с, которая лежит в середине АМВ, пересекала бы а в точке К, то МВ лежала бы в середине угла ОМК и пересекала бы а).

Среди этих прямых Лобачевский выделил две специальные прямые, которые назвал параллельными к данной прямой. Опустим из точки М перпендикуляр на и проведем через точку М прямую /Прямые не пересекаются (рис. 24),

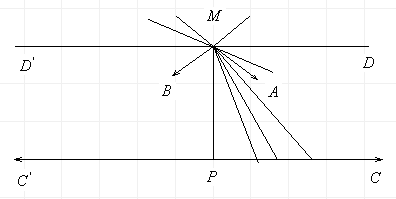
Рассмотрим пучок лучей, которые выходят из точки М и размещены внутри угла Эти лучи можно разбить на два класса: лучи, которые не пересекают прямую , и лучи которые ее пересекают. Лучи первого класса расположены выше лучей второго.

В таком случае существует граничный луч , который разделяет оба класса лучей: все лучи, которые лежат выше этого луча, принадлежат первому классу, а все лучи, которые лежат ниже, принадлежат второму классу. Луч принадлежит первому классу, так как не пересекает прямую .

Определение. Граничная прямая , которая не пересекает прямую , называется параллельной прямой в направлении .

Аналогично, существует граничный луч , который расположен в середине угла и не пересекает . Этот луч симметричен лучу относительно прямой . Прямая , которая содержит этот луч, называется параллельной прямой в направлении .

Таким образом, по Лобачевскому, через данную точку, которая не лежит на ней, можно провести две параллельные прямые. На рисунке 24 направления параллельности изображены стрелками.

Все прямые, которые не пересекают прямую , отличные от параллельных прямых, называются расходящимися. А прямые, которые пересекают прямую , называются сходящимися.

Итак, в отличие от евклидовой плоскости, где прямые делятся на два класса: параллельные и пересекающиеся. В плоскости Лобачевского прямые делятся на три класса: параллельные, сходящиеся и расходящиеся.

Угол , который образуют прямая и с перпендикуляром , называется углом параллельности в точке М относительно прямой (рис.24) . Этот угол для произвольной точки М и произвольной прямой - острый: .