Методические рекомендации

1.Производственная функция Кобба-Дугласа имеет следующий вид:

, (5.1)

где

Y - объем производства (объем выпуска продукции);

K - объем используемых основных производственных фондов (ОПФ);

L - затраты живого труда (численность занятых, объем человеко-часов);

б,в,г - параметры производственной функции, конкретные числовые значения которых определяются методами математической статистики. Это положительные постоянные коэффициенты.

Для линеаризации прологарифмируем уравнение (5.1):

Y₁ = A + бX₁ + вX₂, (5.2)

где

Y₁ = lnY,

A = lnг,

X₁ = lnK,

X₂ = lnL.

Полученная зависимость линейна относительно логарифмов Y, г, K и L, и она может быть оценена как множественная линейная регрессия.

Метод наименьших квадратов применительно к уравнению (5.2) дает следующую систему нормальных уравнений:

УY₁ = nA + бУX₁ + вУX₂

УY₁X₁ = AУX₁ + бУX₁² + вУX₁X₂ (5.3)

УY₁X₂ = AУX₂ + бУX₁X₂ + вУX₂²

Решение этой системы относительно A, б, в позволит получить искомые оценки параметров производственной функции Кобба-Дугласа.

Данные для системы (5.3) удобно представить в виде табл.5.4. При заполнении табл.5.4 вычисления следует выполнять с точностью до четвертого знака после запятой.

Таблица 5.4

Данные для системы нормальных уравнений

i	Y	K	L	Y1=lnY	X1=lnK	X2=lnL	X12	X22	X1X2	Y1X1	Y1X2
1
2
3
4
5
6
7
8
9
10
У	УY	УK	УL	УY1	УX1	УX2	У X12	У X22	УX1X2	УY1X1	УY1X2

Решить систему (5.3) можно любым известным методом. Например, используя метод Крамера, вычислим нужные определители и получим искомые оценки параметров производственной функции Кобба-Дугласа следующим образом:

A = lnг, поэтому для определения величины технологического коэффициента г выполним потенцирование:

г = e^A

2.Проверка адекватности (истинности) построенной производственной функции Кобба-Дугласа называется верификацией модели.

Проверка модели на адекватность по F‑критерию Фишера позволяет определить статистическую значимость коэффициента детерминации R².

Обычный коэффициент детерминации (без поправки) рассчитывается по формуле:

,

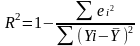где

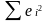- сумма квадратов отклонений наблюдений Y_i от линии регрессии;

- сумма квадратов отклонений наблюдений Y_i от среднего значения Y.

Расчеты рекомендуется выполнять в форме табл.5.5.

Таблица 5.5

Данные для расчета коэффициента детерминации

i	Yi	Ki	Li	=гKiбLiв		ei2
1
2
3
4
5
6
7
8
9
n=10
У	[УYi]	[УKi]	[УLi]		[Уei = 0]	[Уеi2]
У/n						[уост2]	[уо2]

Для определения статистической значимости коэффициента детерминации R² рассчитывается F‑статистика:

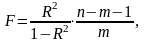
где

n - число наблюдений (n=10);

m - число объясняющих переменных (m=2).

Если выполнены предпосылки относительно ошибок, то величина F имеет распределение Фишера с (m;n-m-1) степенями свободы.

При заданном уровне значимости по таблицам распределения Фишера находим критическое значение F_кр. В данном случае для 5%-ного уровня значимости б и степеней свободы соответственно m=2 и (n‑m-1)=10-2-1=7 критическое значение

Гипотеза о равенстве нулю одновременно всех параметров линейной регрессии, за исключением свободного члена, отвергается, если F > F_кр. В этом случае можно сделать вывод об адекватности модели по F‑критерию Фишера и построенную модель можно использовать для анализа и прогнозирования.

3.Воспользовавшись исходными данными и данными табл.5.5, в единой системе координат построить эмпирическую и теоретическую линии регрессии:

,

где

t - номер года рассматриваемого периода.

По результатам работы сделать выводы.

Работа 6. РАСЧЕТ ОСНОВНЫХ ЭКОНОМИЧЕСКИХ ХАРАКТЕРИСТИК ПРОИЗВОДСТВА ПО ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ КОББА-ДУГЛАСА

Цель: получить практические навыки эконометрического анализа производства.