Контрольные вопросы

1. Выполнение каких свойств данных предполагается при оценивании уравнения регрессии методом наименьших квадратов ?

2. Какими свойствами должны обладать оценки параметров эконометрической модели ?

3. Как проверить статистическую значимость параметров линейной регрессии ?

4. Свойства оценок параметров, полученных методом наименьших квадратов.

5. Чем обусловлена необходимость включения в эконометрические модели случайной составляющей ? Назовите основные причины ошибок модели и раскройте их сущность.

6. Что такое стандартная ошибка оценок параметров модели ?

7. Какие факторы влияют на величину стандартных ошибок параметров парной линейной регрессии ?

8. Раскройте содержание понятия “доверительный интервал для параметра регрессии”.

Задание

1.Оценить дисперсии оценок параметров регрессии.

2.Используя Т-тест Стьюдента, с надежностью Р = 0.95 проверить статистическую значимость оценок параметров регрессии.

3.Определить доверительные интервалы для параметров регрессии.

Для выполнения работы воспользоваться исходными данными и оцененным уравнением регрессии из работы 1.

Методические рекомендации

1.Оценки дисперсий оценок параметров регрессии рассчитываются по формулам:

;

,

где

- оценка дисперсии оценки ;

- оценка дисперсии оценки ;

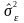- несмещенная оценка дисперсии ошибок :

;

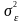e_i - отклонения расчетных значений от наблюдаемых;

n - размер выборки (количество наблюдений);

k - количество оцененных параметров (в нашей модели k = 2, т.к. мы оценивали 2 параметра: b₀ и b₁).

Расчеты рекомендуется выполнять в форме табл.3.1.

Таблица 3.1

Данные для расчета оценок дисперсий

i	Xi	Yi	Xi2			еi2
1
2
...
n
У	УXi	УYi	УXi2		Уei = 0	Уеi2
У/n

2.Значимость параметров регрессии, определенных методом наименьших квадратов, проверяется с помощью Т‑теста Стьюдента.

Для оценки i-того параметра рассчитывается t‑статистика:

,

где

- оценка параметра b_i, полученная методом наименьших квадратов;

- оценка стандартной ошибки (оценка стандартного отклонения) оценки параметра b_i.

Значение t‑статистики сравнивается с табличным критическим значением (t_с), которое определяется по таблицам t‑распределения Стьюдента при заданном доверительном уровне и степенях свободы (n‑k).

В данном случае при доверительном уровне 0.95 и степенях свободы n‑k=15‑2=13 критическое значение: t_с = t_0.95(13) = 2.16.

Если

-t_с < t_bi^* < t_с,

делается вывод о том, что с заданной вероятностью оценка является статистически незначимой.

В противном случае, когда | | > t_c, она является статистически значимой, т.е. оценка параметра статистически достоверно отличается от нуля.

3.Доверительные интервалы для параметров регрессионной модели - это такие интервалы, в которые с заданной вероятностью (в данном случае 95%) попадают истинные значения параметров регрессии.

Доверительные интервалы для параметров позволяют связать оценки параметров с их истинными значениями и рассчитываются по формуле:

.

По результатам работы сделать выводы.

Работа 4. ПРОГНОЗИРОВАНИЕ ПО ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ С ДВУМЯ ПЕРЕМЕННЫМИ

Цель: научиться по модели делать прогнозы и оценивать точность этих прогнозов.