
- •Общие указания
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Контрольные вопросы
- •Задание
- •Методические рекомендации
- •Литература
Контрольные вопросы
В чем заключается оценка качества эконометрической модели ?
Из каких элементов состоит оценка качества эконометрической модели ?
Сущность статистического качества эконометрической модели.
Что такое адекватность модели ?
Как определяются дисперсия остатков, общая дисперсия и дисперсия регрессии? Какая между ними связь?
Что характеризует коэффициент детерминации ?
Для чего используется F-критерий ?
Как оценить достоверность коэффициента корреляции ?
Задание
1.По результатам наблюдений оценить тесноту связи между переменными Y и X:
с помощью коэффициента корреляции;
с помощью коэффициента детерминации;
с помощью корреляционного отношения.
2.Проверить построенную в работе 1 регрессионную модель на адекватность по F-критерию Фишера.
Для выполнения работы воспользоваться исходными данными и оцененным уравнением регрессии из работы 1.
Методические рекомендации
1.Для оценки тесноты линейной связи между Y и X используется коэффициент корреляции:
 .
.
Для оценки тесноты связи при любой форме связи между Y и X используется корреляционное отношение:
 ,
,
где
R2 - коэффициент детерминации, показывающий долю общей колеблемости Y, которая объясняется колеблемостью фактора Х:
 ;
;
 -
межгрупповая дисперсия, отражающая
влияние только учтенных факторов (в
данном случае - Х) на колеблемость Y:
-
межгрупповая дисперсия, отражающая
влияние только учтенных факторов (в
данном случае - Х) на колеблемость Y:
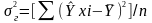 ;
;
 -
общая дисперсия, отражающая влияние
всех факторов (как учтенных, так и не
учтенных) на колеблемость Y:
-
общая дисперсия, отражающая влияние
всех факторов (как учтенных, так и не
учтенных) на колеблемость Y:
 .
.
Малые значения R2 свидетельствуют о плохой аппроксимации данных.
Расчеты рекомендуется выполнять в форме табл.2.1.
Таблица 2.1
Данные для оценки тесноты связи между Y и X
i |
Xi |
Yi |
Xi*Yi |
Xi2 |
Yi2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
У |
УXi |
УYi |
УXiYi |
УXi2 |
УYi2 |
|
|
|
У/n |
|
|
|
|
|
|
уг2 |
уо2 |
2.Проверка модели на адекватность по F-критерию Фишера позволяет определить статистическую значимость коэффициента детерминации R2.
Она выполняется в несколько этапов.
Этап 1. Определяем расчетное значение F‑статистики.
Для парной регрессии расчетное значение F‑статистики вычисляется по формуле:
 ,
,
где
n - количество наблюдений (в данном задании n = 15).
Из этого соотношения следует, что малым значениям F‑статистики (отсутствие значимой функциональной связи X и Y) соответствуют малые значения R2 (плохая аппроксимация данных).
Этап 2. Задаем уровень значимости (уровень ошибки) б (или б.100%).
Например, если мы считаем, что возможная ошибка б для нас составляет 0.05 (или 5%), это означает, что мы можем ошибиться не больше, чем в 5% случаев, а в 95% случаев (или в 100.(1 - б)%) наши выводы будут правильными.
Пусть уровень значимости б = 0.05, т.е. допускаем 5%-ный риск ошибиться.
Этап 3. По статистическим таблицам F‑распределения Фишера с (1,n-2) степенями свободы (для парной регрессии) и уровнем доверия 100.(1 - б)% находим критическое значение (Fкр).
В данном случае при n=15 по статистическим таблицам F‑распределения Фишера для 5%-ного уровня значимости б и степеней свободы соответственно 1 и n‑2=15‑2=13 критическое значение Fкр = Fб(1,n-2) = F0.05(1,13) = 4.67.
Этап 4. Если F > Fкр, то построенная регрессионная модель с риском ошибиться не больше, чем в б.100% случаев, адекватна реальной действительности и в этом случае можно сделать вывод об адекватности принятой модели статистическим данным по F‑критерию Фишера.
Малые значения F‑статистики говорят об отсутствии значимой функциональной связи X и Y.
По результатам работы сделать выводы.
Работа 3. ПРОВЕРКА НАДЕЖНОСТИ ОЦЕНОК ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ
Цель: освоить методику статистического анализа оцененного уравнения регрессии.
