5 Лабораторна робота 5

"Синтез і дослідження типової одноконтурної системи регулювання"

Мета роботи – синтез і дослідження типової одноконтурної системи регулювання.

Теоретичні відомості

Синтез систем автоматичного управління полягає у виборі такої структури САУ, яка забезпечуватиме перехідні процеси з оптимальним співвідношенням прямих показників якості у всіх її контурах регулювання. Найпростіше це завдання вирішується, якщо прив'язати до об'єкта управління пристрій, що управляє, таким чином, що в результаті загальна структура даної САУ матиме вигляд системи підпорядкованого регулювання з послідовною корекцією ( рис. 5.1 )

Рисунок 5.1 – Структурна схема системи підпорядкованого регулювання з послідовною корекцією

Після цього можна без значних розрахунків вибрати параметри регуляторів, що забезпечують відповідність системи вищеназваним вимогам. Найбільш поширеними критеріями оптимізації і налаштування систем підпорядкованого регулювання з послідовною корекцією є модульний і симетричний оптимуми. Для налаштування системи підпорядкованого регулювання на модульний оптимум (МО) необхідно відповідну передаточну функцію об’єкта управління підставити у формулу

,

де і – порядковий номер зовнішнього контура.

Результатом буде передаточна функція регулятора, на підставі якої можна робити висновки про закон регулювання, необхідний для забезпечення оптимального співвідношення прямих показників якості в даному контурі й відповідності перехідному процесу фільтра Баттерворса відповідного порядку. Перевагою модульного оптимуму є оптимальний за швидкодією перехідний процес із найкращим співвідношенням прямих показників якості, проте в системах, налагоджених на МО, можливе виникнення статичної помилки вихідного сигналу за наявності навантаження на об’єкт управління. Для усунення цього недоліку можна забезпечити налаштування системи на МО. Для цього спочатку необхідно налаштувати всі контури регулювання цієї системи на МО, а після цього в зовнішній контур регулювання додати ПІ - регулятор із коефіцієнтами налаштування такими, що знаменник передаточної функції нової системи повинен дорівнювати знаменнику одного з фільтрів Баттерворса. У результаті такого налаштування статична помилка вихідного сигналу буде відсутня, але можливе погіршення значень основних прямих показників якості перехідного процесу. Потрібно зазначити такий факт: якщо попередня процедура послідовної корекції і налаштування системи на модульний оптимум виконана правильно, тобто передаточні функції всіх контурів регулювання відповідають передаточним функціям фільтра Баттерворса, тоді коефіцієнти налаштування відповідного ПІ-регулятора, необхідного для симетричного оптимуму системи, дорівнюватимуть

де і – порядковий номер зовнішнього контура.

Хід роботи

1 Для об’єкта регулювання з передаточною функцією , параметри якого вказуються викладачем з табл. А.4. Передаточна функція регулятора в даному випадку . Для визначення параметрів ПІ-регулятора та необхідно зібрати схему (рис. 5.2) в Matlab та підібрати таке , щоб час перехідного процесу становив 6 мс.

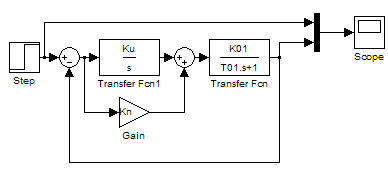
Рисунок 5.2 – Схема для визначення параметрів ПІ-регулятора

2 Для об’єктів регулювання з передаточними функціями

визначити параметри ПІ-регулятора з передаточною функцією , використовуючи табл. А.3.:

;

W0(p)	Умови застосування	Критерій	Параметри регулятора
			Kp	Tи
1	2	3	4	5
K02/(T02р+1)*(T03p+1)	T03‹4T02	МО	Т03/2К02*Т02	Т03
	T03›4T02	СО	Т03/2К02*Т02	4Т02
K03/(T04p+1)*p	-------------	МО	1/2К03*Т04	--------
	-------------	СО	1/2К03*Т04	4Т04

Необхідно врахувати, що для моделювання регулятора його структуру доречно подати у вигляді двох складових і (рис. 5.3).

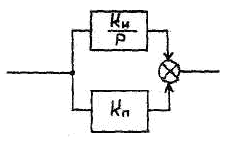
Рисунок 5.3 – Структура ПІ-регулятора

3 Зібрати схему об’єкта регулювання з передаточною функцією , виставивши параметри і , відповідно до вашого варіанта. Подайте на вхід об’єкта ступінчастий вхідний сигнал (рис. 5.4). Отриману осцилограму перехідного процесу і осцилограму вхідного сигналу наведіть у звіті. Виміряйте час перехідного процесу і порівняйте амплітуди вхідного й усталеного значень вихідного сигналу, результати занести до звіту.

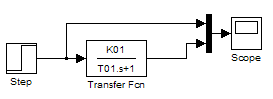
Рисунок 5.4 – Структурна схема об’єкта регулювання

4. Не змінюючи амплітуди вхідного сигналу, охопіть модель об’єкта управління одиничним від’ємним зворотнім зв’язком. При цьому вхідний сигнал необхідно подавати через суматор (рис. 5.5). Отриману осцилограму перехідного процесу і осцилограму вхідного сигналу наведіть у звіті. Виміряйте час перехідного процесу і порівняйте амплітуди вхідного і усталеного значень вихідного сигналу, результати занести до звіту.

Рисунок 5.5 – Структурна схема об’єкта регулювання з одиничним від’ємним зворотнім зв’язком

5 Зібрати схему замкненої системи регулювання, з’єднавши послідовно моделі об’єкта і регулятора, й охопити їх зворотним зв’язком (рис. 5.2). Подайте на вхід системи регулювання ступінчастий вхідний сигнал з тією самою амплітудою, що і в попередніх пунктах. Отриману осцилограму перехідного процесу й осцилограму вхідного сигналу наведіть у звіті. Виміряйте час перехідного процесу, результати занести до звіту. Визначте, як залежить час перехідного процесу t_p з T₀₁.

6 Зібрати схему об’єкта регулювання з передаточною функцією , виставивши параметри відповідно до вашого варіанта. Подайте на вхід об’єкта ступінчастий вхідний сигнал (рис. 5.6). Отриману осцилограму перехідного процесу і осцилограму вхідного сигналу приведіть в звіті. Виміряйте час перехідного процесу і перерегулювання, результати занести до звіту.

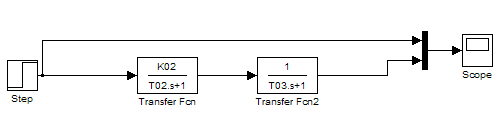
Рисунок 5.6 – Структурна схема об’єкта регулювання

7. Не змінюючи амплітуди вхідного сигналу, охопіть модель об’єкта управління одиничним від’ємним зворотним зв’язком. При цьому вхідний сигнал необхідно подавати через суматор (рис. 5.7). Отриману осцилограму перехідного процесу і осцилограму вхідного сигналу наведіть у звіті. Виміряйте час перехідного процесу і перерегулювання, результати занести до звіту.

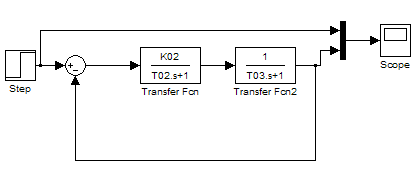
Рисунок 5.7 – Модель об’єкта управління з одиничним від’ємним зворотнім зв’язком

7. Зібрати схему замкненої системи регулювання, з’єднавши послідовно моделі об’єкта і регулятора, й охопити їх зворотним зв’язком (рис. 5.8). Подайте на вхід системи регулювання ступінчастий вхідний сигнал з тією самою амплітудою, що і в попередніх пунктах. Отриману осцилограму перехідного процесу й осцилограму вхідного сигналу наведіть у звіті. Виміряйте час перехідного процесу і величину перерегулювання, результати занести до звіту. Визначте, як залежить час перехідного процесу t_p з T₀₂.

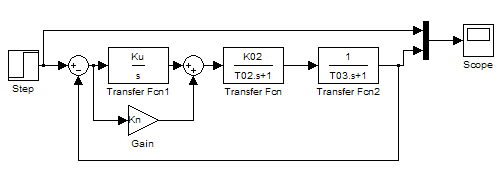
Рисунок 5.8 – Структурна схема замкненої системи регулювання

7. Подайте на вхід ланки з більшою сталою часу ступінчастий вхідний сигнал через суматор (рис. 5.9). Отриману осцилограму перехідного процесу зі збурення наведіть у звіті. Визначте статичну похибку .

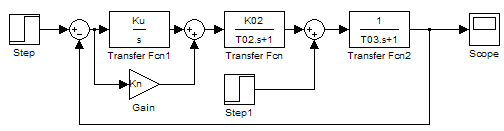
Рисунок 5.9 – Структурна схема замкнутої системи регулювання

7. Не змінюючи параметрів регульованого об’єкта, експериментальним шляхом визначити, як впливає зміна коефіцієнтів і регулятора на вигляд перехідних процесів з керування і збурення. Наведіть у звіті отримані осцилограми перехідних процесів і вкажіть їх статичні похибки.

8. Зібрати схему замкненої системи регулювання, з’єднавши послідовно моделі об’єкта і регулятора з виставленими коефіцієнтами при налаштуванні за критерієм МО, й охопити їх зворотним зв’язком (рис. 5.10). Подайте на вхід системи регулювання ступінчастий вхідний сигнал. Отриману осцилограму перехідного процесу наведіть у звіті. Виміряйте час перехідного процесу і величину перерегулювання, результати занести до звіту. Визначте як залежить час перехідного процесу t_p з T₀₄.

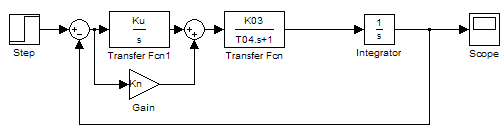
Рисунок 5.10 - Структурна схема замкненої системи регулювання з виставленими коефіцієнтами при налаштуванні за критерієм МО

7. Подайте на вхід інтегральної ланки ступінчастий вхідний сигнал через суматор (рис 5.11). Отриману осцилограму перехідного процесу зі збурення за відсутності керуючого сигналу наведіть у звіті. Визначте статичну похибку .

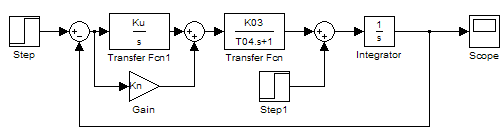
Рисунок 5.11 – Структурна схема замкненої системи регулювання за відсутності керувального сигналу

7. Зібрати схему замкненої системи регулювання, з’єднавши послідовно моделі об’єкта і регулятора з виставленими коефіцієнтами при налаштуванні за критерієм СО, й охопити їх зворотним зв’язком (рис. 5.10). Подайте на вхід системи регулювання ступінчастий вхідний сигнал. Отриману осцилограму перехідного процесу за керувальною дією наведіть у звіті. Виміряйте час перехідного процесу і величину перерегулювання, результати занести до звіту. Визначте, як залежить час перехідного процесу t_p з T₀₄.

8. Подайте на вхід інтегральної ланки ступінчастий вхідний сигнал через суматор (рис 5.11). Отриману осцилограму перехідного процесу зі збурення за відсутності керувального сигналу наведіть у звіті.

Питання для перевірки та контролю

1 Назвіть основні види типових збурень.

2 Що розуміють під законом регулювання?

3 Назвіть види регуляторів і їх основні параметри.

4 Які переваги має ПІ – регулятор?

5 Як впливає замикання систем на її якість?

6 Як визначити передаточну функцію регулятора при настроюванні контура на модульний та симетричний оптимуми?

7 Як виконується синтез послідовної коригувальної ланки?

СПИСОК ЛІТЕРАТУРИ

1. Лукас В. А. Теория автоматического управления. – М. : Недра, 1990.

2. Теорія автоматичного керування. М. Г. Попович, О. В. Ковальчук.– К. : Либідь, 2007.

3. Классические методы автоматического управления / Б. Я. Лурье, П. Дж. Энрайт; под ред. А. А. Ланнэ. – СПб. : БХВ-Петербург, 2004. – 640 с.

4. Никулин Е. А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем: учеб. пособие для вузов.– СПб. : БХВ-Петербург, 2004. – 640 с.

ДОДАТОК А

(обов’язковий)

Варіанти завдань до лабораторних робіт

Таблиця А.1 – Значення коефіцієнтів відповідно до варіанта для л. р. № 2

№ вар.	К	Кос	К02	Т02	№ вар.	К	Кос	К02	Т02
1	0,6	-0,2	0,5	0,008	16	0,4	-1,6	3	0,025
2	0,83	-1,66	4	0,025	17	0,25	-0,5	3	0,009
3	0,34	-0,67	2	0,009	18	2,5	-1,25	0,5	0,04
4	3,3	-1,1	0,5	0,025	19	0,8	-0,4	0,4	0,007
5	0,2	-0,2	2	0,008	20	2,86	-1,43	0,4	0,04
6	3,32	-1,66	0,5	0,002	21	0,54	-0,67	3	0,007
7	2,01	-0,67	0,5	0,008	22	4,8	-1,2	0,5	0,04
8	4,4	-1,1	1	0,002	23	0,6	-1,8	3	0,02
9	0,1	-0,2	3	0,008	24	2,13	-0,71	0,5	0,008
10	1,6	-1,6	0,5	0,04	25	0,5	-1,25	5	0,0125
11	0,72	-1,43	4	0,0125	26	0,6	-0,4	0,8	0,006
12	0,2	-0,4	4	0,009	27	0,7	-1,4	2	0,04
13	0,36	-0,71	4	0,006	28	1,42	-0,71	0,8	0,009
14	2,22	-1,11	0,8	0,04	29	6,64	-1,66	0,4	0,0125
15	4,2	-1,4	0,8	0,025	30	0,9	-1,8	4	0,04

Продовження додатка А

Таблиця А.2 – Значення коефіцієнтів відповідно до варіанта для л. р. № 3

№ вар.	К1	К2	№ вар.	К1	К2
1	0,3	2,25	16	0,1	0,25
2	0,6	2,25	17	1,04	1,69
3	1,32	4,84	18	0,34	2,89
4	1,44	5,76	19	2	6,25
5	1,38	5,29	20	0,32	2,56
6	0,32	0,16	21	0,56	1,96
7	1,68	4,41	22	1,56	6,76
8	1,26	4,41	23	2,08	6,76
9	1,86	9,61	24	0,64	0,64
10	0,8	4	25	1,36	2,89
11	0,26	1,69	26	0,84	4,41
12	2,16	7,29	27	0,36	3,24
13	2,24	7,84	28	1,62	7,29
14	0,76	3,61	29	0,28	1,96
15	0,08	0,16	30	0,88	4,84

Продовження додатка А

Таблиця А.3 – Значення коефіцієнтів відповідно до варіанта для л. р. № 4

№ вар-та	К1	К2	К3	№ вар-та	К1	К2	К3	№ вар-та	К1	К2	К3
1	0,3	0,25	1,8	18	1,2	1,44	0,2	35	1,0	4	1
2	0,32	0,16	1,8	19	0,9	2,25	0,2	36	1,28	2,56	0,4
3	0,4	0,16	1,6	20	0,96	1,44	0,2	37	1,5	6,25	0,8
4	1,2	4	0,4	21	1,4	1,96	0,5	38	18	3,24	0,1
5	0,32	0,16	1,2	22	1,32	4,84	0,4	39	1,5	6,25	0,4
6	0,4	0,16	1,8	23	0,4	0,25	2	40	1,68	7,84	0,5
7	1,74	8,41	0,2	24	1,4	1,96	0,2	41	1,74	8,41	1,2
8	0,4	0,25	1,6	25	1,44	5,76	0,8	42	1,6	4	0,4
9	0,5	0,25	1,8	26	0,64	0,64	1,6	43	1,8	9,0	1,4
10	0,48	0,64	1,6	27	0,88	1,21	0,4	44	1,68	7,84	0,2
11	0,4	0,25	2	28	1,44	5,76	0,4	45	1,8	9,0	0,8
12	0,5	0,25	2	29	1,8	3,24	0,2	46	1,8	9,0	0,2
13	0,72	1,44	0,4	30	0,88	1,21	0,2	47	0,48	0,64	1,8
14	0,64	0,64	2	31	1,12	1,96	0,5	48	1,76	4,84	0,5
15	1,2	1,44	0,4	32	1,5	6,25	0,8	49	1,8	3,24	0,3
16	0,78	1,69	2	33	1,28	2,56	0,8	50	1,8	3,24	0,4
17	0,96	1,44	0,4	34	1,8	3,24	0,5	51	1,8	9,0	0,4

Продовження додатка А

Таблиця А.4 – Значення коефіцієнтів передаточної функції відповідно до варіанта для л. р. №5

№ варіанта	Т01	К01	Т02	Т03	К02	Т04	К03
1	0,02	2	0,005	0,008	0,2	0,005	10
2	0,0125	16	0,005	0.025	5	0,005	38
3	0,02	4	0,005	0,008	0,25	0,005	12
4	0,0125	6	0,005	0,0125	0,25	0,005	30
5	0,02	8	0,005	0,008	0,4	0,005	14
6	0,0125	5	0,005	0,125	2	0,005	45
7	0,02	10	0,005	0,008	0,5	0,005	15
8	0,0125	4	0,005	0,125	5	0,005	44
9	0,02	16	0,005	0,009	0,2	0,005	16
10	0,0125	10	0,005	0,1	4	0,005	50
11	0,02	20	0,005	0,009	0,25	0,005	20
12	0,0125	2	0,005	0,009	0,4	0,005	24
13	0,02	8	0,005	0,1	10	0,005	48
14	0,0125	4	0,005	0,009	0,5	0,005	25
15	0,02	5	0,005	0,0125	0,2	0,005	28
16	0,0125	12	0,005	0,0125	0,5	0,005	35
17	0,02	2	0,005	0,025	1	0,005	42
18	0,0125	10	0,005	0,0125	0,4	0,005	32
19	0,02	20	0,005	0,05	5	0,005	60
20	0,0125	20	0,005	0,05	1	0,005	40

ДОДАТОК Б

(обов’язковий)

Зразок титульного аркуша

Міністерство освіти і науки, молоді та спорту України

Сумський державний університет

Кафедра комп’ютерних наук

Секція комп’ютеризованих систем управління

Звіт

з лабораторної роботи 1

з дисципліни "Теорія автоматичного управління"

Викладач Бага Л. М.

Студент групи СУ – 01 Іванов І. І.

Варіант №

Суми 2012

57