26. Дискретный случай

Пусть X есть дискретная случайная величина с возможными значениями x₁, x₂ , … и p_k = P(X = x_k). Число  называется в случае абсолютной сходимости ряда i-м начальным моментом случайной величины X (или ее распределения)(i=1,2,...).

Число

μi =	∑	(xk − ν1)ipk
	k

называется центральным i-м моментом X.

Особое значение имеют первый начальный момент ν₁ и второй центральный момент μ₂.

Математическое ожидание

Первый начальный момент

ν1 =	∑	xkpk
	k

называется математическим ожиданием X и обозначается МX. Математическое ожидание определяет положение центра распределения в следующем смысле: если считать p_k массами, помещенными в точках x_k действительной оси, то МX есть как раз координата центра тяжести этой системы.

Свойства математического ожидания

1) математическое ожидание постоянной а равно этой постоянной: Ma = a.

2) математическое ожидание суммы равно сумме математических ожиданий

M(X₁ + X₂) = MX₁ + MX₂.

3) математическое ожидание произведения постоянной величины на случайную величину равно произведению постоянной на математическое ожидание случайной величины: M(aX) = aMX.

4) математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:  .

Пример 1: Биномиальное распределение с параметрами n, p:

.

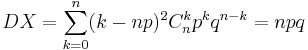Дисперсия

Второй центральный момент называется дисперсией случайной величины Х и обозначается через DX, т.е.

DX =	∑	(xk − MX)2pk = M(X − MX)2
	k

Для вычисления дисперсии часто полезна следующая формула: DX = MX² − (MX)².

Корень квадратный из дисперсии называется разбросом или стандартным отклонением, или средним квадратическим отклонением и обозначается через σx:  .

Свойства дисперсии

1)Дисперсия постоянной величины равна нулю: Da = 0.

2)Дисперсия произведения постоянной величины на случайную величину равна произведению квадрата постоянной величины на дисперсию случайной величины: D(aX) = a²DX.

3)Дисперсия суммы постоянной а и случайной величин равна дисперсии случайной величины: D(a + X) = DX.

4) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X₁ + X₂) = DX₁ + DX₂.

Пример 2 Биномиальное распределение:  .

27. Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Слабый закон больших чисел

Пусть есть бесконечная последовательность (последовательное перечисление) одинаково распределённых и некоррелированных случайных величин  , определённых на одном вероятностном пространстве  . То есть их ковариация  . Пусть  . Обозначим   выборочное среднее первых  членов:

.

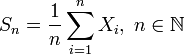Тогда  .

Усиленный закон больших чисел

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин  , определённых на одном вероятностном пространстве  . Пусть  . Обозначим   выборочное среднее первых   членов: . Тогда   почти наверное.

25. Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Будем обозначать случайные величины буквами латинского алфавита X, Y, Z

Случайная величина бывает: дискретной дискретная случайная величина принимаетконечное (или счетное) число возможных значений- x_i (где i = 1.. n или i = 1 .. ∞) с определенными вероятностями. Пример: игральные кости. Выпадаемый номер - случайная величина, которая может принимать одно из возможных значений - 1, 2, 3, 4, 5 или 6 с равной вероятностью*.непрерывной непрерывная случайная величина может принимать все значения из некоторого кон ечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка,бесконечно. Пример: рост студентов - рост студента может принимать любое значение из числового промежутка 1 м до 2,5 м. Число возможных значений - бесконечно. Закон распределения дискретной случайной величины

Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.

Закон распределения можно задать таблично, аналитически (в виде формулы) или графически (в виде многоугольника распределения).

Рассмотрим случайную величину X, которая принимает значения x₁, x₂, x₃ ... x_n с некоторой вероятностью p_i, где i = 1.. n. Сумма вероятностей p_iравна 1.

Таблица соответствия значений случайной величины и их вероятностей вида

называется рядом распределения дискретной случайной величины или просто рядом распределения. Эта таблица является наиболее удобной формой задания дискретной случайной величины.

Графическое представление этой таблицы называется многоугольником распределения.  По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.