Анализ данных

Поскольку в качестве единицы измерения мы выбрали минуту, размерностью коэффициента остывания r будет мин^-1.

Чтобы получить максимально приближённые к экспериментальным данным значения температуры, в программу был добавлен цикл, в ходе которого менялись значения параметра r от 0 до 1 с шагом 0.01. В файл выводились значения разницы между экспериментальным значением температуры в момент времени t = 15 и значением, полученным программой и значение коэффициента r. В результате можно было сделать вывод, что минимальное отклонение полученного значения температуры от экспериментального наблюдается при r = 0.04. Это значение коэффициента является правдоподобным. При r = 0.0908937 наблюдается минимальное отклонение значений на первом шаге, однако в момент времени t = 15 разница составляет около 30 градусов.

Так как используя закон Ньютона мы получили результаты, которые близки к экспериментальным данным, можно сделать вывод, что этот закон применим к чашке с кофе.

При r=0.04 остывать до 52,5 градусов чашка будет 17.3 минуты, до 37,25 градусов – 34.5 минуты, до 29.625 градусов – 51.8 минут

Точность и устойчивость метода Эйлера

Для изучения точности метода Эйлера можно воспользоваться аналитическим решением дифференциального уравнения.

(7)

Заметим, что T(t = 0) = T_s - (T_s - T₀) = T₀, а T(t   ) = T_s.

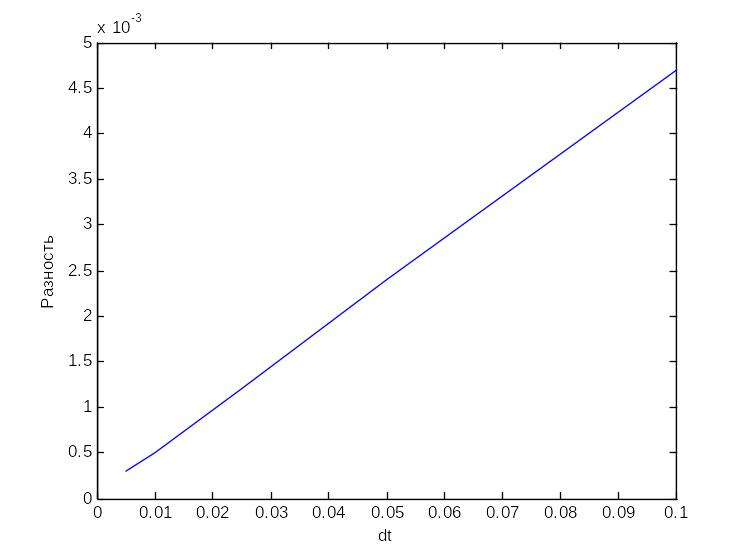
Рисунок 3 Зависимость разности от временного шага

С помощью программы Coffee вычислим температуру в момент t=1 мин с шагами 0.1, 0.05, 0.025, 0.01, 0.005. Для первого шага выберем значение r=0.0908937 Метод Эйлера является методом второго порядка.

	r=0.04 численное решение	точное решение	Разность
0.1	80.6035	80.6082	0.0047
0.05	80.6058	80.6082	0.0024
0.025	80.607	80.6082	0.0012
0.01	80.6077	80.6082	0.0005
0.005	80.6079	80.6082	0.0003

Какой необходимо выбрать величину шага чтобы достигалась точность 0,1% в момент времени t=5 ?

при r=0.04 значение точного решения = 71.9426

t=0.1 temp=71.7229 dif= 0.219741 - 0.305439%

t=0.05 temp=71.8327 dif= 0.10989 - 0.152747%

t=0.025 temp=71.8876 dif= 0.054959 - 0.0763928%

t=0.0125 temp=71.9151 dif= 0.027492 - 0.0382138%

t=0.00625 temp=71.9288 dif= 0.0137582 - 0.0191238%

Точность в 0.1% достигается уже при шаге =0.025.

Выводы:

В лабораторной работе был смоделирован процесс остывания чашки с кофе. Решение дифференциального уравнения было полученно с помощью метода Эйлера. Согласно построенной модели был найден ответ на вопрос «что лучше - добавить молоко сразу после приготовления кофе или немного подождать, прежде чем добавлять молоко?» - молоко лучше добавлять после, т.к. до 80 градусов кофе остывает за 3.9 минуты, а при добавлении молока с 85 до 75 градусов кофе остывает за 4.3 минуты.