Логические основы эвм
Современные вычислительные машины могут выполнять не только арифметические, но и логические операции. Машина производит определённое преобразования над двоичными числами в результате которого, получается двоичное число, которое является результатом выполнения соответствующей логической операции.
В основе логических схем и устройств ЭВМ лежит специальный математический аппарат, который называется математической логикой. Используется только начальный раздел, который называется алгеброй логики или булевой алгеброй.
Булевая алгебра занимается исчислением высказываний (Буль 1815 – 1866 гг.).
Высказывание - это утверждение, о котором можно сказать: оно ложно или истинно. В булевой алгебре содержимым высказывания не интересуются, а интересуются лишь их истинностью или ложностью.
Из нескольких простых высказываний с помощью союзов И, ИЛИ, НЕ можно составить сложное (составное) высказывание, которое тоже будет истинно или ложно. Если высказывание истинно, то его обозначают логической единицей, а если ложно, то логическим нулем.
Пример: Москва стоит на Неве –0 –ложное высказывание
Ленинград стоит на Неве-1- истинное высказывание
Москва стоит на Неве (ложное высказывание) ИЛИ Ленинград стоит на Неве (истинное высказывание) в результате получается истинное высказывание .
Таким образом, значение высказываний можно рассматривать, как переменную величину, которая принимает два дискретных значения '' 0 '' или '' 1 '' – это приводит к полному соответствию между логическими высказываниями в математической логике и двоичными цифрами в двоичной системе исчисления. Это позволяет описывать работу логических схем и проводить их анализ и синтез с помощью математического аппарата алгебры логики.
Общий вид логических функций
Н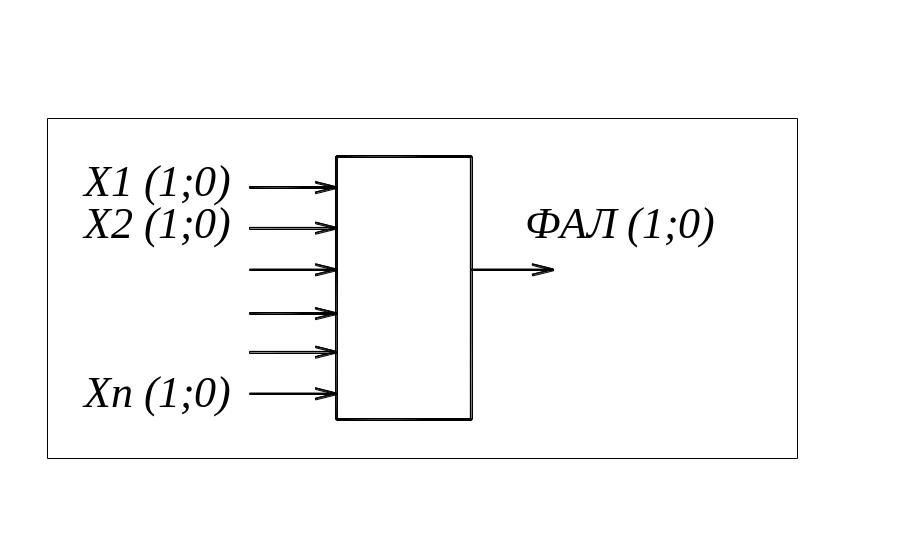
а
вход подаются логические переменные
X1....Хn,
которые могут принимать значения 0 или
1.
На выходе получаем функции алгебры логики (ФАЛ) f (x1, x2, … , xn) = (0;1), которые также могут принимать значения 0 или 1.
Связь между входными переменными X1 ... Хn и функциями алгебры логики f (x1, x2, … , xn) может быть представлена аналитическим или табличным способом.
При аналитическом способе, связи между логическими переменными представляются в виде логических уравнений. Этот способ достаточно компактен, но труден для восприятия человека и используется при большом количестве входных переменных.
При табличный способе – связь между входными переменными представляется в виде таблицы. Этот способ более прост и нагляден, но при большом количестве входных переменных становится громоздким и трудно поддаётся анализу.
Строго доказано, что количество возможных наборов входных переменных зависит от количества этих переменных. Для “n” переменных существует К=2n наборов входных переменных.
X1 |
X2 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
Общее число логических функций, которые могут быть получены при n логических переменных, равно 2К.
Например: при n=2, К=4 общее число логических функций будет равно 24=16. При n=3, К=8 общее число логических функций будет равно 28=256.
Таблица логических функций для двух логических переменных (Х1,Х2)
-
X1
X2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
9 (X1 X2 )=X1^ X2 (конъюнкция, логическое умножение, логическое И) – функция 9 =1 при X1 =1, X2 =1, в остальных случаях равна нулю.
X1 |
X2 |
9 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 1 = 0
1 0 = 0
1 1 = 1
8(X1
X2 ) = X1
X2
- отрицание
конъюнкции (функция Шеффера,) –
функция 8 = 0 при X1 = 1, X2 = 1, в остальных случаях функция равна 0.
Правила выполнения логического отрицания ИЛИ: 0 0 =1
0 1 =1
1 0 =1
1 1 =0
15 (X1 X2 ) =X1 X2– дизъюнкция (логическое сложение, операция ИЛИ) – функция 15 =0 при X1 =0 и X2 = 0 , в остальных случаях 15 =1.
2(X1
X2 )= X1
X2
- отрицание
дизъюнкции, функция 2
=
1 при X1 = 0 и
X2 = 0 , в остальных
случаях 2
=0.
10(X1 X2 ) =X1 X2 - эквивалентность (равнозначность) – функция 10 =1 при X1 =X2, в остальных случаях 10 = 0.
7
(X1 X2
) =X1 X2
– отрицание эквивалентности
(равнозначности) - функция 7=
0 при X1
= X2, в остальных
случаях 7
= 1.
12 (X1 X2 ) = X1X2 - импликация X1 в X2 , функция 12 = X2 при X1 =1, в остальных случаях 12 = 1.
14 (X1 X2 ) = X2 X1 - импликация X2 в X1 , функция 14 = X1 при X2 =1, в остальных случаях 14 = 1.
5
(X1
X2
) = X1X2
– отрицание импликации
X1 в X2
, функция 5
= X2
при
X1 =1, в остальных
случаях 5
= 0.
3 (X1 X2 ) = X2X1 – отрицание импликации X2 в X1 , функция 5 = X1 при X2 =1, в остальных случаях 3 = 0.
1 (X1 X2 ) = 0 - при любых значениях переменных X1 и X2
16 (X1 X2 ) = 1 - при любых значениях переменных X1 и X2
13 (X1 X2 ) = X1 - при любых значениях переменных X1 и X2
11 (X1 X2 ) = X2 - при любых значениях переменных X1 и X2
4
(X1 X2
) = X1 - при
любых значениях переменных X1
и X2
6 (X1 X2 ) = X2 - при любых значениях переменных X1 и X2