6.4.3 Способы организации индексируемого массива

Индексом называется набор адресов и ключей записей, которые выбираются из основного массива по определённому закону [1—2]. Отдельный элемент набора индексов также называется индексом, хотя это не соответствует значению слова index — список.

Существуют три разновидности индексов.

«Плотная» (сплошная) индексация — индексируется каждый элемент массива.

«Разреженная» (индексно-последовательная) индексация — индексируется группа элементов массива.

«Селективная» (рандомизированная) индексация — индексируется подмножество элементов

Сплошной индекс. Сплошной индекс связан с созданием инвертированного массива ключевых атрибутов к основному массиву. Простейшая организация инвертированного массива показана на рис. 6.15.

Элементы, составляющие инвертированный массив, называются группами. Каждая группа содержит значение ключевого атрибута, имеющееся в массиве, и набор адресов записей, содержащих этот ключ. Сами группы являются записями неопределенной длины.

В информационно-поисковых системах ключевые атрибуты соответствуют ключевым словам, определяющим тематику документа (например, статьи). Количество ключевых слов для статьи может быть любым. Связь основного и инвертированного массивов в этом случае показана на рисунке 6.16.

Рис. 6.15 — Пример организации инвертированных массивов

по двум значениям атрибутов

Основной эффект инвертированного массива проявляется при поиске данных по нескольким условиям. Пусть дан запрос «Найти все статьи, содержащие ключевые слова А и С». Система обратится к инвертированному массиву и найдет группы ключей А и С. Совпадающие значения адресов в этих группах укажут в данном примере на искомую запись с адресом 150 (рис. 6.16).

Логические связки в запросах могут быть любыми, и с математической точки зрения требуемые поисковые операции есть операции пересечения, объединения, вычитания над множествами адресов, которые хранятся в группах, названных в запросе.

Так, при обработке запроса «Найти все записи, содержащие ключи Е или С, кроме А», которому в терминах теории множеств соответствует запись (EC)\A, производится последовательное вычисление ({100, 150, 240}{150, 240})\{150, 220} = = {100, 240}.

Результат означает, что запросу удовлетворяют записи с адресами 100 и 240 (рис. 6.16).

Рис. 6.16 — Уплотнение инвертированного массива

Следует отметить, что поиск по инвертированному массиву обнаруживает только адреса записей и плохо приспособлен для указания всех ключей, связанных с найденной записью. Между тем, эта информация часто запрашивается. В одном примере запись с адресом 150 была найдена по значениям ключей А и С очень быстро, но определить, есть ли в этой записи третий ключ Е, используя только инвертированный массив, очень трудно.

Индексно-последовательный массив (К-индекс). Индексно-последовательный массив представляет собой последовательный массив, отсортированный по значениям ключевого атрибута, к которому создается дополнительный массив индексов.

В индекс выносится информация о записях, номера которых образуют арифметическую прогрессию с шагом d > 1, причём первый индекс адресует первую запись. Основной массив, дополненный таким индексом, обычно называется индексно-последовательным.

Индексы такого типа называются К-индексами (от слова «ключ»). Шаг арифметической прогрессии для К-индексов равен: , где М — количество элементов в исходном массиве.

Рандомизированный индекс (А-индекс). Если ключи записей, информация о которых выносится в индекс, приближенно образуют арифметическую прогрессию, получаем ситуацию с адресной функцией для индекса (рандомизация индекса), причём первый индекс адресует первую запись.

Индексы такого типа называются А-индексами (от слова «адрес»).

Точное описание рандомизированного индекса состоит в следующем. А-индекс с номером i хранит адрес записи основного массива, ключ которой равен или непосредственно больше значения

p₁ + z(i – 1),

где z — константа (шаг арифметической прогрессии), р₁ — значение ключа первой записи основного массива.

Точной формулы для шага арифметической прогрессии z для А-индексов не существует, обычно рекомендуют:

z  2 max (p_i – p_i – 1).

Рассмотрим пример построения К- и А-индексов для массива со следующими значениями ключей (табельный номер рабочего): 40, 6, 46, 10, 50, 43, 16, 53, 52, 17, 22, 16, 72, 71, 31, 36, 65, 25, 87, 89.

Предварительно необходимо упорядочить по возрастанию исходный массив. Массив будет иметь следующий вид (рис. 6.17, а). Для построения К- и А-индексов необходимо вычислить шаг арифметической прогрессии d, z.

Для К-индексов шаг прогрессии равен: ; принимаем d = 5. Для А-индексов max (p_i – p_i – 1) = 15, следовательно, можно взять z = 30.

В А-индексе можно не хранить значение ключа адресуемой записи, так как оно легко вычисляется по формуле:

p_i  p₁ + z(i – 1).

При формировании А-индекса первое значение индекса А₁ соответствует значению ключа p₁ = 06, следовательно, А₁ = 0100.

p₂  p₁ + z = 36 (в исходном массиве такое значение есть, его и выбирают)  А₂ = 107. Далее, p₃  p₁ + 2z = 66 (т.к. в исходном массиве такого значения ключа нет, то выбирают следующее большее, т.е. 71)  А₃ = 116 и т.д.

Рис. 6.17 — Организация данных:

а — основной массив; б — индексно-последовательная;

в — рандомизация индекса

Организация поиска с использованием К-индекса

Если массив снабжен К-индексом, то поиск значения q ведется в две стадии:

1) в массиве индексов, который отсортирован в силу упорядоченности основного массива;

2) среди записей, расположенных между двумя соседними индексами, найденными на первой стадии.

При поиске записи с ключом q сначала находится индекс К_i, такой, что K_i  q < K_i+1 (i — номер индекса в массиве индексов). Далее поиск продолжается в основном массиве, начиная с адреса, определённого в индексе K_i.

Требуемое число сравнений для массива с использованием К-индексов составляет:

где М — число записей в массиве.

Организация поиска с использованием А-индекса

Рассмотрим поиск с использованием рандомизированных индексов. На первом этапе номер требуемого далее А-индекса определяется по формуле:

,

где q — искомое значение, ключевой признак для поиска; z — разность значений ключей для A-индексов (шаг арифметической прогрессии); [ X ] — функция округления числа X до целого в меньшую сторону; p₁ — значение ключа первой записи.

Интервал записей на втором этапе поиска определяется номерами (адресами) записей, указанными в i-м и (i + 1)-м А-индексах. Поиск в этом интервале ведется бинарным методом. На вычисление величины i сравнения не тратятся, поэтому эффективность поиска с применением A-индексов в случае массива оценивается:

,

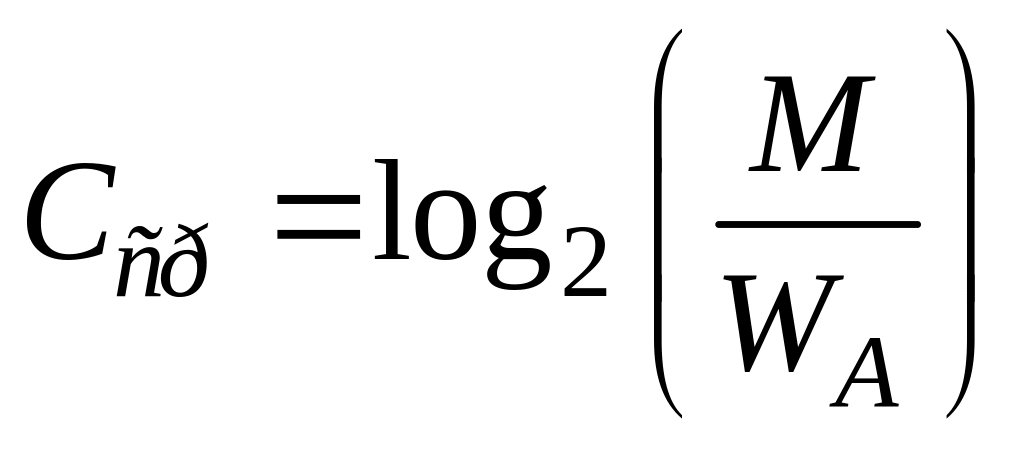где W_A — количество А-индексов в массиве.

Сравнение формул показывает, что поиск в массиве с А-индексами осуществляется быстрее, чем с К-индексами. Время поиска быстро уменьшается с ростом W_А, что соответствует уменьшению z. Однако при выборе малых значений z возможны случаи, когда соседние А-индексы относятся к одной и той же записи (разность ключей соседних записей намного больше z), и увеличение числа индексов W_A не сопровождается дальнейшим сокращением времени поиска.

Выбор шага d для K-индексов основан на соответствии применяемого в этом случае алгоритма поиска и двухступенчатого поиска, рассмотренного ранее. Исследования показывают, что оптимальное .

Индексы обоих типов используют дополнительную память сверх объема, занятого собственно данными, причем А-индексы используют объемы памяти несколько меньше. Это зависит от величины разброса значений ключевых реквизитов.

Организация корректировки в К- и А- индексах

При корректировке записей индексы также должны изменяться: всегда изменяются К-индексы и значительно реже — А-индексы.

При включении новой записи с ключом q определяется К-индекс, такой, что K_i – 1  q  K_i, где i — номер K-индекса. Затем все К-индексы с номером i и больше (i+1, i+2 и т.д.) принимают значения ключей и адресов тех записей, которые непосредственно предшествуют ранее зафиксированным в этих индексах записям.

Аналогично при удалении записи с ключом q все К-индексы с номером i и больше принимают значения ключей и адресов тех записей, которые непосредственно следуют за ранее указанными в этих индексах записями.

Примеры. Вставим в исходный массив запись с ключом 20.

Удалим из исходного массива запись с ключом 50.

Рассмотрим корректировку массива, снабженного А-индексами. При вставке в массив записи с ключевым атрибутом q индекс A_i будет адресовать новую запись лишь тогда, когда р₁ + z (i – 1)  q  p_k, и не изменится в остальных случаях.

Как правило, при корректировке изменяется только одно значение A-индекса, а не несколько, как это характерно для К-индексов.

Таким образом, А-индексы целесообразнее К-индексов — они характеризуются меньшим объемом памяти, необходимым для их размещения, а также более быстрым поиском при достаточно большом М.