6.3 Нелинейная организация данных

Нелинейная организация данных — множество записей, каждая из которых связана с произвольным количеством предшествующих и последующих записей. Наиболее используемыми вариантами нелинейной организации данных являются деревья, нелинейные списки.

6.3.1 Древовидная организация данных

Древовидной организацией данных (деревом) называется множество записей, расположенных по уровням следующим

образом (рис. 6.8):

1. на первом уровне расположена только одна запись (корень дерева);

2. к любой записи i-го уровня ведёт адрес связи только от одной записи (i – 1)-го уровня.

Количество уровней в дереве называется рангом. Записи дерева, которые адресуются от общей записи (i – 1)-го уровня, образуют группу.

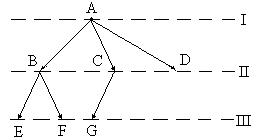
Рис. 6.8 — Древовидная организация данных

Максимальное число элементов в группе называется порядком дерева.

Пример размещения дерева в памяти компьютера показан на рисунке 6.9.

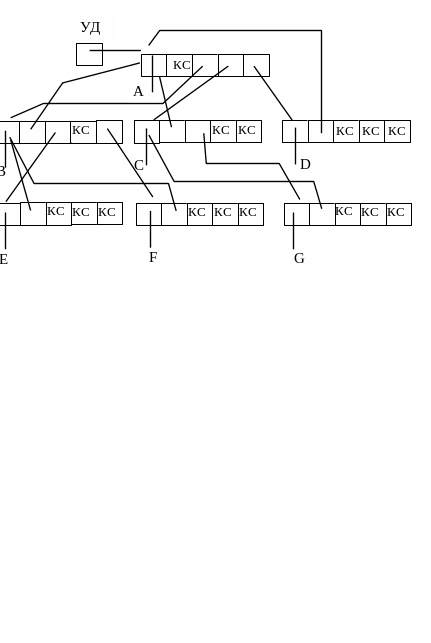
Рис. 6.9 — Размещение (представление) дерева

в памяти компьютера

Назовем звеном связи набор адресов связи, принадлежащих одной записи.

Если порядок дерева равен р, то все звенья связи состоят из (р + 1)-го адреса (один адрес — обратный). Корень дерева адресуется из специального указателя дерева. Незанятые адреса связи содержат признак конца списка КС.

В представленном выше дереве группами являются множества записей {B,C,D}, {E,F}, {G}. Порядок этого дерева равен 3, и ранг тоже равен 3.

При размещении дерева в памяти ЭВМ каждая запись может занимать произвольное место и все записи связаны через адреса связи.

Деревья обычно формируются двунаправленными, адpec связи от записи уровня (i + 1)-го к записи i-го уровня называется обратным.

Рассмотрим бинарные деревья. Эти деревья имеют порядок, равный 2, и составляющие их записи могут быть упорядоченными. Для этого один из атрибутов записи должен быть объявлен ключевым.

Чтобы определить понятие упорядоченности бинарных деревьев, требуется ввести ряд вводных понятий. В качестве примера рассмотрим бинарное дерево, полученное из массива с ключевыми атрибутами: 25, 10, 20, 38, 18, 42, 5, 23, 60, 31 (рис. 6.10). Запись со значением 25 — корень дерева.

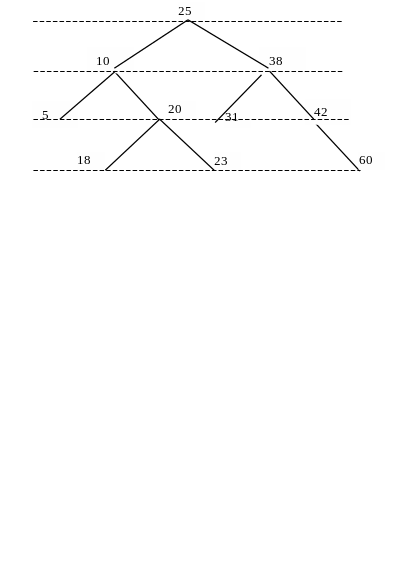
Рис. 6.10 — Упорядоченное бинарное дерево

Записи, у которых заполнены два адреса связи, называются полными. Записи с одним адресом называются неполными. Записи с двумя незаполненными адресами называются концевыми. На рисунке 6.10 записи со значениями 25, 10, 20, 42 — полные; 38 — неполная запись; 5, 18, 23, 31, 60 — концевые.

Адреса связи делятся на левые и правые. Так, адрес со значениями от 20 к 18 — левый, от 20 к 23 — правый. Правую (левую) ветвь записи образует поддерево, адресованное из этой записи через правый (левый) адрес связи. У записи со значением 38 правая ветвь состоит из записей 42, 31, 60; левая ветвь — пустая.

В упорядоченном бинарном дереве каждый элемент на своей левой ветви имеет элементы с меньшими, чем у него значениями ключей, а на правой ветви — элементы с большими значениями ключей. Это определение позволяет также различать левые и правые адреса (ветви).

Упорядоченное бинарное дерево формируется из неупорядоченного массива записей по определенному алгоритму.

Алгоритм построения упорядоченного бинарного дерева:

1. первая запись массива с ключом А₁ становится корнем дерева;

2. значение ключа второй записи А₂ сравнивается с А₁, находящемся в корне дерева;

3. если А₂ < А₁, то вторая запись помещается на левой от корня ветви, в противном случае — на правой ветви;

4. далее на каждом шаге создается упорядоченное дерево из первых i записей;

5. выбор места i-й записи массива в дереве производится следующим образом. Ключ А_i сравнивается с корневым значением и выполняется переход по левому адресу, если А₁ > А_i. Если А₁  А_i, то — по правому адресу. Ключ, записанный по этому адресу, сравнивается с А_i, и снова организуется переход по левому или правому адресу до нахождения свободного места. Если требуемый адрес не заполнен, то он должен адресовать запись с ключом А_i.

Итак, описанный алгоритм позволяет строить упорядоченное бинарное дерево из одной записи, затем из первых двух, первых трех и так далее до исчерпания всех записей массива.

При формировании упорядоченного бинарного дерева производится сравнение пар признаков:

C_ср = 1,4  M  log₂M,

где M ― число записей исходного массива, для которых строится дерево.

Рассмотрим основные операции, выполняемые над записями в дереве: поиск и корректировка данных (включение, исключение записей).

Поиск. В процессе поиска данных по совпадению в упорядоченном бинарном дереве просматривается путь, начинающийся всегда в его корне.

Алгоритм поиска данных в бинарном дереве:

1. искомое значение q сравнивается со значением корня А₁;

2. если А₁ = q, то запись, соответствующая корню, помещается в поле результата и производится сравнение значения q и значения ключа вершины, лежащей справа от корня дерева А₁;

3. если А₁ > q, то дальнейшее сравнение q производится с вершиной, лежащей по левой дуге корня;

4. если А₁ < q, то по правой дуге корня;

5. для произвольной вершины дерева А_i результаты сравнения означают:

• А_i = q — запись, соответствующая вершине, помещается в поле результата, и путь продолжается по правой дуге А_i;

• А_i > q — производится сравнение q с вершиной, лежащей по левой дуге А_i;

• А_i < q — производится сравнение q с вершиной, лежащей по правой дуге А_i.

Поиск заканчивается, когда в какой-либо вершине А_j отсутствует адрес связи, необходимый для дальнейшего продолжения поиска.

Для алгоритма поиска по совпадению в произвольном бинарном дереве среднее число сравнений пар признаков равно: C_ср = 1,4 log₂ M.

Корректировка. Включение новой записи при корректировке бинарного дерева означает отработку одного шага алгоритма формирования дерева с включаемой записью на входе. Исключение записи зависит от того, какая запись исключается: концевая, неполная или полная. Адрес связи на исключаемую концевую запись заменяется на символ КС (конец списка). В неполной записи адрес связи заменяется на её собственный адрес связи.

При исключении полной записи решается задача о подстановке на её место другой записи, такой, что ее ключ не нарушает общей упорядоченности бинарного дерева, — такие записи называются соседними. Соседняя слева запись — это запись с ключом, который непосредственно меньше ключа данной записи, а ключ соседней справа записи равен или непосредственно больше, чем ключ данной записи. Способ нахождения соседней справа записи очень простой. Если исключаемая запись имеет ключ q, то от нее происходит переход по правой ветви дерева и производится поиск от достигнутой записи значения q. Любая соседняя запись (рекомендуется выбирать соседнюю запись с большей длиной ветвей) пересылается на место исключаемой связи, а соседняя запись исключается, и вторая соседняя запись от исключаемой записи перераспределяется заново в дерево.

Ранг упорядоченного бинарного дерева можно сократить с помощью специальных преобразований — подравниваний. Преобразованное дерево называется подравненным.

Назовём длиной ветви дерева разность между максимальным уровнем записи этой ветви и уровнем записи, определяющим эту ветвь. Так, на рис. 6.10 у записи со значением 38 длина левой ветви — 0, длина правой ветви — 2.

Если для некоторой записи длины ее ветвей различаются не более чем на 1, то она называется сбалансированной. Бинарное дерево называется подравненным, если все его записи являются сбалансированными. Чтобы перейти от произвольного бинарного дерева к подравненному дереву, надо для каждой несбалансированной записи найти соседнюю слева запись, если у нее левая ветвь длиннее правой, или найти соседнюю справа запись, если правая ветвь длиннее. Найденная соседняя запись помещается на место несбалансированной, а сама несбалансированная запись заново включается в дерево. После такого преобразования разность длин ветвей сократится. Эти действия производятся со всеми несбалансированными записями. Лучшая последовательность преобразования ветвей — от корня по возрастанию номеров уровней.

Дерево на рис. 6.10 не является подравненным. Чтобы данное дерево стало подравненным, нужно найти запись со значением 38 и соседнюю справа к записи 38 и поместить её на место записи 38, а запись 38 заново включить в дерево. После таких преобразований разность длин ветвей сокращается и, как правило, ранг дерева уменьшается.

В случае необходимости подравниваний полной записи дерева выполняют следующие действия:

1. сначала выбирается соседняя запись с большей длиной ветвей. Эта соседняя запись со всеми выходящими из неё записями помещается на место подравниваемой (и, следовательно, предварительно исключаемой записи);

2. далее, вторая соседняя запись вместе с исходящими из неё записями исключается из дерева и заново перераспределяется в дерево по алгоритму включения новой записи;

3. в последнюю очередь перераспределяется (т.е. заново включается в дерево) подравниваемая запись. Эти действия проводятся со всеми записями, нарушающими подравненность.

Во время проведения процедуры подравниваний дерева после включения-исключения некоторых записей условия подравненности часто нарушаются, поэтому процедуру балансировки дерева обычно проводят в несколько итераций.

В подравненном дереве число сравнений пар признаков при поиске записи равно: С_ср = 1,04  log₂M. Максимальное число сравнений ограничивается C_мах = 1,44  log₂ M.

Как правило, корень дерева не подравнивается, т.к. после подравниваний всех записей дерева оно становится подравненным и относительно корня дерева.

Но бывают такие случаи, когда в исходном дереве сразу же виден существенный перекос по длине правой и левой ветвей относительно корня дерева, тогда надо сразу же корень дерева подравнять в первой итерации.

В древовидной организации данных связь любой записи с N записями, составляющими ее группу, реализуется с помощью N адресов связи. Возможно, однако, связать все записи группы в цепочку и адресовать с предшествующего уровня первую запись группы. Таким образом, получается новая нелинейная организация данных — нелинейный список.