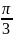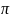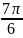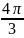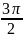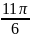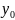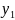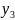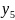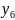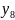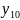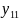3. Сезонная волна

Сезонность, как правило, связывается исключительно со сменой природно – климатических условий в рамках ограниченного промежутка времени – годового периода. Наиболее ярко эта связь видна там, где исследуемые процессы прямо связаны с естественными особенностями того или иного времени года: в сельском хозяйстве, добывающих отраслях, отраслях легкой промышленности, обрабатывающих сельскохозяйственную продукцию и др. Однако сезонные колебания формируются не только под влиянием природно-климатических факторов, но и, пусть в меньшей мере, под влиянием иных особенностей системы, уходящих корнями в экономику.

Под сезонными колебаниями понимают регулярные, периодические наступления внутригодовых подъемов и спадов производства, связанных со сменой времени года, а под сезонностью – ограниченность годового периода работ под влиянием того же природного фактора.

Оценки коэффициентов пропорциональности могут быть получены следующим образом:

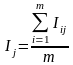, (21)

где – постоянная пропорциональности для j-го месяца, не меняющаяся от года к году;

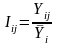(22)

– индексами сезонности.

Рассматривают не просто ряд из относительных величин , а ряд процентов, по которому строится сезонная волна:

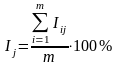(23)

3. Аналитическая волна с использованием рядов Фурье

Рассмотрим теперь другой способ нахождения сезонной составляющей использующей ряд Фурье в качестве аналитической модели сезонности. В этом виде уравнение Фурье запишется следующим образом

(24)

В этом уравнении определяет номер гармоники ряда Фурье. От числа учтенных гармоников зависит степень точности данной аналитической модели. Обычно используются от 1 до 4 гармоник в зависимости от необходимой точности и формы сезонной составляющей. Для нахождения параметров уравнения используется метод наименьших квадратов.

(25)

Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, решение которых дает следующие формулы для вычисления параметров:

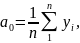
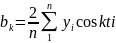(26)

Как видно из формулы (26) параметры уравнений зависят от 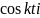и .

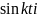Для изучения сезонных колебаний на протяжении года необходимо взять n = 12. Тогда представляя периоды как части длины окружности ряда динамики можно записать в следующем виде

0

Далее определяется количество необходимых гармоник, и аналитическое выражение сезонной составляющей ( ) найдено.

3. Оценка адекватности и точности в трендовых моделях

Независимо от вида и способа построения экономико-математической модели вопрос о возможности ее применения в целях анализа и прогнозирования экономического явления может быть решен только после установления адекватности, т.е. соответствия модели исследуемому процессу или объекту. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые считаются существенными для исследования.

Трендовая модель 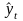конкретного временного ряда 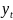считается адекватной, если правильно отражает систематические компоненты временного ряда. Это требование эквивалентно требованию, чтобы остаточная компонента 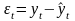(t = 1, 2,…, n) удовлетворяла свойствам случайной компоненты временного ряда: случайность колебаний уровней остаточной последовательности, соответствие распределения случайной компоненты нормальному закону распределения, равенство математического ожидания случайной компоненты нулю, независимость значений уровней случайной компоненты.

Поворотной точкой считается , общее число поворотных точек для остаточной последовательности обозначается через p.

В случайной выборке математическое ожидание числа точек поворота р и дисперсия выражаются формулами:

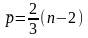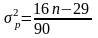; (27)

Критерием случайности с 5%-ным уровнем значимости является выполнение неравенства

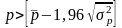, (28)

где квадратные скобки означают целую часть числа. Если это неравенство не выполняется, трендовая модель считается неадекватной.

Проверка равенства математического ожидания случайной компоненты нулю, если она распределена по нормальному закону, осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия задается формулой:

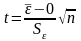, (29)

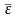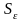где - среднее арифметическое значение уровней остаточной последовательности ; - стандартное (среднеквадратическое) отклонение для этой последовательности.

Если расчетное значение t меньше табличного значения t_α статистики Стьюдента с заданным уровнем значимости α и числом степеней свободы n-1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной.

Вывод об адекватности трендовой модели делается, если все указанные выше четыре проверки свойств остаточной последовательности дают положительный результат.

Для адекватных моделей имеет смысл ставить задачу оценки их точности. Статистическим показателем точности является средняя относительная ошибка аппроксимации

(30)