1.3 Типові налаштування систем керування електроприводами

Найбільш часто на практиці застосовуються налаштування контурів за аперіодичним законом та на модульний і симетричний оптимуми.

При аперіодичному налаштуванні необхідно звести передаточну функцію замкненого контуру до аперіодичної ланки.

Приклад. Здійснити налаштування системи (рис. 1.6) за аперіодичним законом.

Об’єкт керування представлено послідовним з’єднанням інтегратора та аперіодичної ланки з коефіцієнтом передачі k_об та сталою часу T_об. Виконавчий орган – 10е кореговано ланка (підсилювач) k_во.

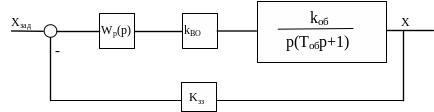
Рисунок 1.6 – Структурна схема системи

Необхідно знайти передаточну функцію регулятора W_p(p), що забезпечує аперіодичне настроювання контуру. Для цього необхідно підібрати такий регулятор, щоб в прямому каналі отримати інтегратор.

Тобто, бажана передаточна функція прямого каналу має бути у вигляді

.

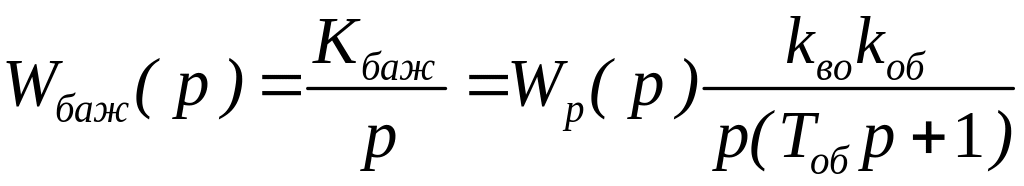Де k_баж – бажаний коефіцієнт підсилення прямого каналу.

Тоді передаточна функція регулятора буде наступною

.

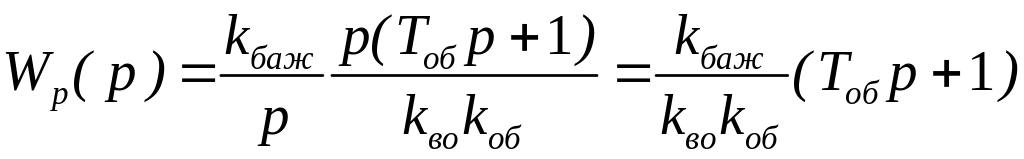Передаточна функція замкненого контуру (рис. 1.6) знаходиться як

.

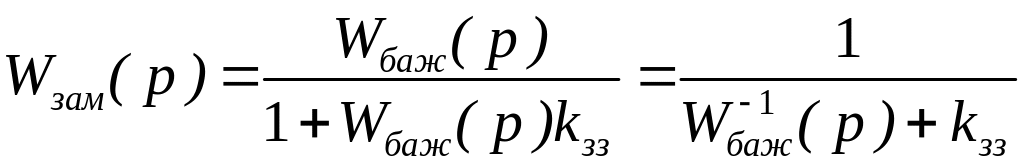Підставимо W_баж(р) в останнє рівняння і отримаємо

.

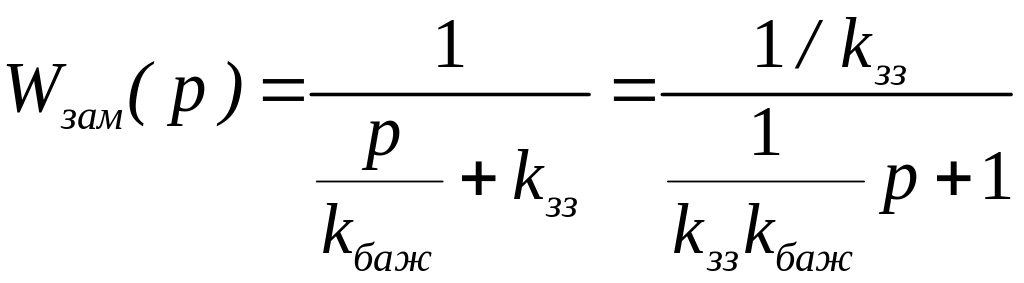Тобто, контур налаштовано за аперіодичним законом. Величиною k_баж задається бажана швидкодія контуру.

Розглянемо настроювання на модульний та симетричний оптимуми.

Для настроювання на модульний оптимум структурну схему замкненого контуру керування необхідно привести до наступного вигляду (рис. 1.7).

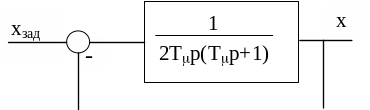
Рисунок 1.7 ― Структурна схема контуру при настроюванні на модульний оптимум

На схемі позначає якусь довільну малу сталу часу.

У цьому випадку перехідна характеристика контуру буде наступною (рис. 1.8).

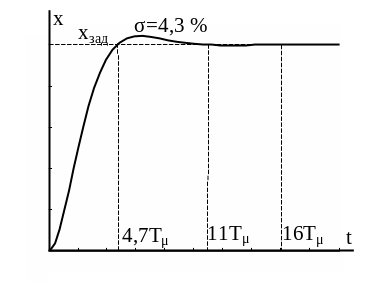
Рисунок 1.8 ― Перехідна характеристика контуру при настроюванні на модульний оптимум

Для настроювання на симетричний оптимум структурну схему контуру керування необхідно трансформувати до вигляду, як показано на рис. 1.9.

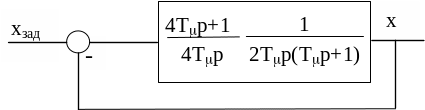
Рисунок 1.9 ― Структурна схема контуру при настроюванні на симетричний оптимум

Перехідна характеристика контуру з настроюванням на симетричний оптимум має 12е корегованого12 43% (рис. 1.10).

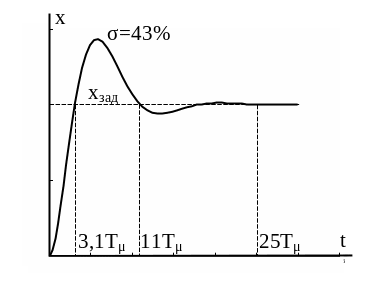
Рисунок 1.10 ― Перехідна характеристика контуру з настроюванням на симетричний оптимум

Настроювання на симетричний оптимум, як правило, використовують в контурах, які містять послідовне з’єднання аперіодичної ланки та інтегратора, щоб забезпечити в контурі нульову статичну похибку. В цьому випадку отримують ПІ-регулятор.

Настроювання на модульний оптимум застосовують в контурах, які складаються з двох послідовних аперіодичних ланок, і в результаті отримують ПІ-регулятор та нульову статичну похибку системи.

Застосування настроювання на модульний оптимум в контурах з послідовним з’єднанням аперіодичної ланки та інтегратора дає П-регулятор і тому є допустимим в системах з певною статичною помилкою.

Розглянемо приклад процедури настроювання на модульний оптимум для контуру на рис. 1.11.

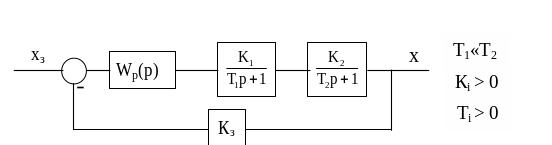
Рисунок 1.11 ― Структурна схема прикладу процедури настроювання

Необхідно визначити передаточну функцію регулятора та її параметри.

Зведемо контур до вигляду з одиничним зворотним зв’язком (рис. 1.12).

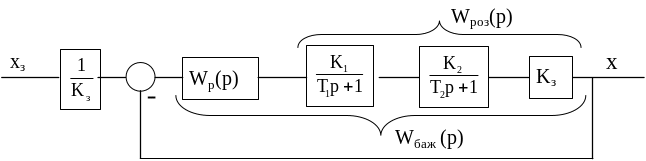
Рисунок 1.12 ― Структурна схема контуру, приведеного до одиничного зворотного зв’язку

Передаточна функція розімкненого 13е корегованого (без урахування регулятора) контуру

.

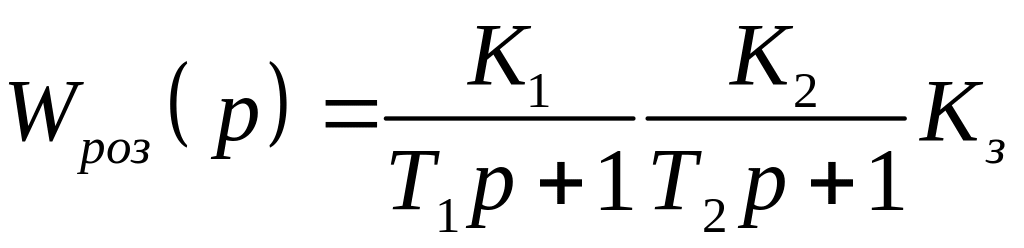Тоді бажана передаточна функція корегованого контуру

.

Приймемо, що є малою сталою часу. Тоді

.

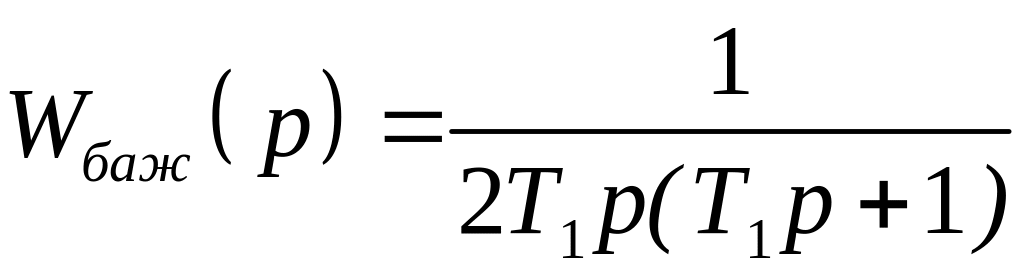Передаточна функція регулятора визначається як

.