§9.3. Задача Коші в n-вимірному просторі

У випадку ‑ вимірного простору фундаментальним розв’язком однорідного рівняння теплопровідності буде функція

,

де ,

а розв’язком задачі Коші

в класі обмежених функцій є

Розв’язок задачі Коші

де функції та є неперервними та обмеженими, набуває вигляду

Практична робота №6 Задача Коші для рівнянь параболічного типу

Приклад П6.1. Нехай для будь-якого при кожному фіксованому . Довести , що функція

є розв’язком задачі Коші:

Доведення. Безпосередньою перевіркою переконаємось в справедливості твердження. Очевидно , що

.

Отже

Крім того

Приклад П6.2. Розв’язати задачу Коші:

Розв’язання. Скористаємось результатами прикладу П6.1. Зведемо початкову умову до однорідної. Для цього введемо заміну де ‑ нова невідома функція. Тоді для функції отримуємо наступну крайову задачу

Тут Тому, згідно прикладу П6.1,

Повертаючись до проведеної заміни, маємо

Відповідь:

Приклад П6.3. Показати, що функція визначена як сума ряду

(П6.1)

який допускає почленне диференціювання потрібне число разів, є розв’язком задачі Коші

Тут .

Розв’язання. Очевидно, що

.

При виконанні умов, які гарантують рівномірну збіжність ряду (П6.1) та рядів, які отримані з нього почленним диференціюванням один раз по і двічі по , для суми даного ряду, отримуємо

(в другому ряді ми поклали ).

Приклад П6.4. Розв’язати задачу Коші

Розв’язання. Проведемо редукцію даної задачі. Розв’язок шукаємо у вигляді

де є роз’язком задачі Коші

а є роз’язком задачі

Згідно прикладу П6.1, маємо

Згідно прикладу П6.3, дістанемо

Отже,

Відповідь:

Приклад П6.5. Нехай , , - розв’язки наступних задач Коші:

Довести, що функція

є розв’язком задачі Коші

де .

Доведення. Очевидно , що

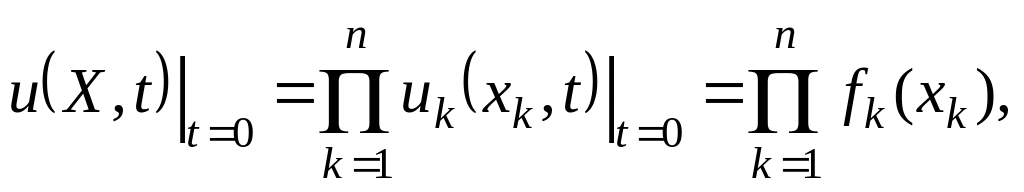
тобто початкова умова виконується. Аналогічно, за допомогою безпосередньої перевірки, маємо

Приклад П6.6. Розв’язати задачу Коші

Розв’язання. Проведемо редукцію даної задачі Коші. Розв’язок шукаємо у вигляді де є розв’язком задачі

а є розв’язком задачі

Згідно прикладу П6.1, дістанемо

,

а шукаємо у вигляді

де, згідно прикладу П6.5, є розв’язком задачі

а є розв’язком задачі

Задача на відшукання функції розв’язана в прикладі П6.4 і

Аналогічно, згідно прикладу П6.3, дістанемо

Отже:

Відповідь:

Завдання для самостійної роботи

I рівень

Розв’язати задачу Коші.

1. ,

.

2. ,

.

3. ,

.

4. ,

.

5. ,

.

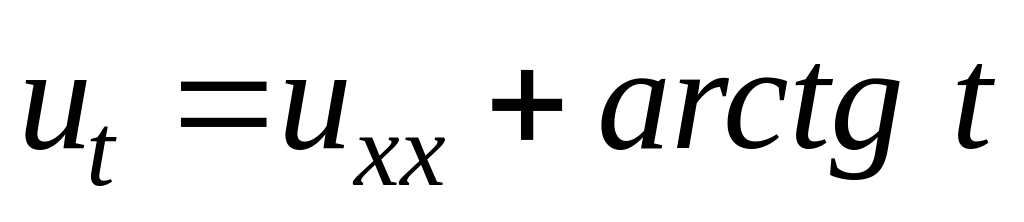II рівень

Розв’язати задачу Коші

1. ,

.

2. ,

.

3. ,

.

Тема 10. Єдиність та стійкість розв’язків крайових задач для рівнянь параболічного типу

§10.1. Єдиність та стійкість розв’язків мішаних крайових задач

Розглянемо в тривимірному просторі деякий об’єм обмежений достатньо гладкою поверхнею . Розглянемо першу мішану крайову задачу для рівняння параболічного типу

, (10.1)

(10.2)

(10.3)

де - точка тривимірного простору; та - задані функції.

При постановці крайових задач вважатимемо, що початкові та граничні умови не суперечливі. Тобто, у випадку першої мішаної крайової задачі виконуються умови узгодження

, .

Теорема 10.1. В класі функцій розв’язок задачі (10.1)-(10.3) єдиний і неперервно залежить від початкових та граничних даних.

Доведення. Припустимо, що існує два розв’язки крайової задачі (10.1)-(10.3) та . Тобто, мають місце наступні співвідношення:

(10.4)

(10.5)

(10.6)

(10.7)

(10.8)

. (10.9)

Тоді, віднімаючи почленно рівняння (10.4), (10.7), початкові умови (10.5), (10.8), граничні умови (10.6), (10.9) отримаємо, що функція є розв’язком крайової задачі

, , (10.10)

, , (10.11)

, . (10.12)

Згідно принципу максимуму (див. тема 7, теорема 7.1) маємо, що при . Отже, . Єдиність доведена.

Нехай функції та є розв’язками рівняння (10.1) і виконуються наступні умови:

, ,

.

Покажемо, що для довільних . Функція є розв’язком однорідного рівняння теплопровідності (10.10) і для неї виконуються умови

, ;

, .

Тоді, згідно наслідку з принципу максимуму (див. §7.2) при всіх буде виконуватися нерівність

.

Отже, , що і треба було довести.

Теорема 10.1 доведена.

Розглянемо граничні умови другого та третього роду

, , ; (10.13)

, , , , (10.14)

де функції та - задані; - коефіцієнт теплопровідності; - коефіцієнт теплообміну.

Теорема 10.2. В класі функцій розв’язок другої (10.1), (10.2), (10.13) та третьої (10.1), (10.2), (10.14) мішаних крайових задач єдиний.

Доведення. Припустимо, що існує два розв’язки відповідних крайових задач та . Тоді функція буде задовольняти однорідне рівняння (10.10), однорідну початкову умову (10.11) та наступну однорідну граничну умову другого (третього) роду:

, , . (10.15)

Розглянемо функцію

. (10.16)

Тоді . Згідно формули Остроградського-Гаусса

Тоді

. (10.17)

Згідно умови (10.15) перший інтеграл в правій частині (10.17) дорівнює нулю у випадку граничної умови другого роду або менший нуля у випадку граничної умови третього роду. Отже, . Але, згідно (10.11) маємо . Отже, функція є невід’ємною, не зростаючою при t і при дорівнює нулю. Тому при . Тобто , . Отже, , що й потрібно було довести.

Теорема 10.2 доведена.