§ 10. Вероятность попадания случайной точки в произвольную область

Перепишем соотношение (**) § 9 так:

Отсюда

N.

заключаем: про­изведение f (I, ц) АхАу есть вероятность попада­ния случайной точки в прямоугольник со сторо­нами Ах и Ау.

АХ

Рис. 17

Пусть в плоскости хОу задана произвольная об­ласть D. Обозначим собы­тие, состоящее в попада­нии случайной точки в эту область, так: (X, Y)<zD. Разобьем область D на п элементарных областей пря-параллельными оси Оу, находящимися на расстоя-.; одна от другой, и прямыми, параллельными оси Ох, сходящимися на расстоянии А у одна от другой (рис. 17) |Для простоты предполагается, что эти прямые пересекают °^НтУр области не более чем в двух точках). Так как

165

события, состоящие в попадании случайной точки в л._е ментарные области, несовместны, то вероятность попад_а ния в область D приближенно (сумма элементарных о§ ластей приближенно равна области D\) равна сум^ вероятностей попаданий точки в элементарные облает^

Р((Х, К)с£>)«2/(6„ т\,)ЬхЬу. Переходя к пределу при Ах—>-0 и &у—»-0, получ_им Р((Х, V)<=D)= JJ/(x, y)dxdy. _(t)

Итак, для того чтобы вычислить вероятность попада. ния случайной точки (X; Y) в область D, достаточно

н айти двойной интеграл по области D от функции fix, у).

Геометрически равенство (*) можно истолковать так: вероятность попадания слу­чайной точки (X; К) в область ~^х D равна объему тела, огра-

N(VT;O)

Рис. 18

ничейного сверху поверхно­стью z — f(x, у), основанием которого служит проекция этой поверхности на плоскость хОу.

Замечание. Подынтегральное выражение / (х, у) dx dy назы­вают элементом вероятности. Как следует из предыдущего, элемент вероятности определяет вероятность попадания случайной точки в эле­ментарный прямоугольник со сторонами dx и dy.

Пример. Плотность распределения двумерной случайной величины

1

Н айти вероятность попадания случайной точки в прямоугольник

(рис. 18) с вершинами К (I; 1), L (У 3; 1), Л* (I; 0) и ЛМ Решение. Искомая вероятность

dxdy =

dx

_{^"1 нЬ"}²_{1 г}

о

L _* £L . J_

" 12' 4~48"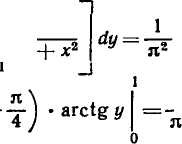

1 /я

(О)

VI 1

Г dy __ J 1+V

166

§11. Свойства двумерной плотности вероятности

Свойство 1. Двумерная плотность вероятно-^_и неотрицательна:

⁽ f(x,y)>0.

доказательство. Вероятность попадания случай­ной точки в прямоугольник со сторонами Ах и Ау есть неотрицательное число; площадь этого прямоугольника — положительное число. Следовательно, отношение этих двух чисел, а значит, и их предел (при Ах—>-0 и Ау—►О), который равен / (х, у) (см. § 9), есть неотрицательное число, т. е.

fix, у)>0.

Заметим, что свойство непосредственно следует из того, что F(x, у)—неубывающая функция своих аргументов

(И)-

Свойство 2. Двойной несобственный интеграл с бес­конечными пределами от двумерной плотности равен единице:

J f(x, y)dxdy=\

Доказательство. Бесконечные пределы интегри­рования указывают, что областью интегрирования служит вся плоскость хОу, поскольку событие, состоящее в том, что'случайная точка попадет при испытании на плоскость хОу, достоверно, то вероятность этого события (она и определяется двойным несобственным интегралом от дву­мерной плотности) равна единице, т. е.

f (х, y)dxdy^\.

Пример. Задана плотность совместного распределения непрерыв-^Ной Двумерной случайной величины (X, Y): f (х, у) = С cos x cos у в квадрате ОвЦх^п/2, 0<у«Сл/2; вне этого квадрата f(x,y)=O. ^Найти постоянный параметр С.

Решение. Воспользуемся свойством 2, учитывая, что х и у вменяются от 0 до л/2:

00 00

С \ \ cos х cos у dxdy=l.

— 00 —X

167

Отсюда

(л/2 я/2 \

\ cos xdx \ cos У dy). о о /

Выполнив интегрирование, получим искомое значение парамет ра С=1.