§ 3. Функция распределения двумерной случайной величины

Рассмотрим двумерную случайную величину (X, Y) (безразлично, дискретную или непрерывную).

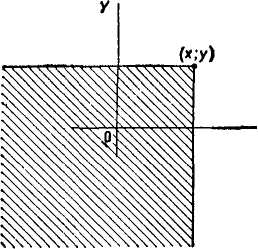
Пусть х, у—пара действи­тельных чисел. Вероятность события, состоящего в том, , что X примет значение, мень­шее х, и при этом Y примет значение, меньшее у, обоз--* начим через F (х, у). Если х и у будут изменяться, то, вообще говоря, будет изме­няться и F {х, у), т. е. F(x, у) есть функция от х и у.

Рис. 13

Функцией распределения двумерной случайной вели­чины (X, Y) называют функцию F (х, у), определяющую для каждой пары чисел х, у вероятность того, что л примет значение, меньшее х, и при этом Y примет зна­чение, меньшее у:

F(x,y) = P(X<x, Y<y).

Геометрически это равенство можно истолковать так-F (х, у) есть вероятность того, что случайная точка (X, У>

158

_лопад^{ет в} бесконечный квадрант с вершиной (х, у), рас-_оЛоженный левее и ниже этой вершины (рис. 13).

Пример. Найти вероятность того, что в результате испытания оставляющая X двумерной случайной величины (X, Y) примет зна­чен¹¹⁶ X < 2 и при этом составляющая Y примет значение Y < 3, если известна функция распределения системы

/ 1 х 1 \ / 1 ц 1 \

F (х, У) — 1 — arctg -S-4--O- * [-=■ ^arotg -Т+-О- •

Решение. По определению функции распределения двумерной случайной величины,

F(x,y)=P(X<x, Y <у). Положив х = 2, у = 3, получим искомую вероятность

/1 2 1 \

Р(Х < 2, Y <3) = F(2, 3) = — arctg ——|-—- X

3,1\ ( \ я,1\ I \ л , 1 \ 3 3_9

⁼Т' Т~Тб'

§ 4. Свойства функции распределения двумерной случайной величины

Свойство 1. Значения функции распределения удовлетворяют двойному неравенству

Доказательство. Свойство вытекает из определе­ния функции распределения как вероятности: вероят­ность— всегда неотрицательное число, не превышающее единицу.

Свойство 2. F (х, у) есть неубывающая функиия по каждому аргументу, т.е.

F (^X2> y)^F (x_t, у), если х₂ > х{, F (х, у₂) > F (x, r/j), если у_г > у_х.

Доказательство. Докажем, что F (х, у)—неубы­вающая функция по аргументу х. Событие, состоящее ^в том, что составляющая X примет значение, меньшее х_г, ^и при этом составляющая У < у, можно подразделить на ^следук>щие два несовместных события:

1. X примет значение, меньшее х_х, и при этом Y < у ^с вероятностью Р (X < х_и У < у);

2. X примет значение, удовлетворяющее неравенству

j, и при этом У < у с вероятностью Р(х_х^

У<у).

,159

По теореме сложения, Р(Х<х₂, У<у) = Р(Х<х_и Отсюда

Р(Х<х_г, У<у) — Р(Х<х_1г

или

Любая вероятность есть число неотрицательное, поэтому F(x₂, у)— F(x_u у)>0, или F (х₂, y)^ F (х_х, у),

что и требовалось доказать.

Свойство становится наглядно ясным, если восподь. зоваться геометрическим истолкованием функции распре-деления как вероятности попадания случайной точки в бесконечный квадрант с вершиной (х; у) (рис. 13). При возрастании х правая граница этого квадранта сдвигается вправо; при этом вероятность попадания случайной точки в «новый» квадрант, очевидно, не может уменьшиться.

Аналогично доказывается, что F (х, у) есть неубыва­ющая функция по аргументу у.

Свойство 3. Имеют место предельные соотношения:

1) F(-oo,y) = 0, 2) F (х, -оо) = 0,

3) F( — оо, — оо) = 0, 4) F(co, oo)= 1.

Доказательство. 1) F (— оо, у) есть вероятность события X < — оо и Y < у; но такое событие невозможно (поскольку невозможно событие Х< — оо), следовательно, вероятность этого события равна нулю.

Свойство становится наглядно ясным, если прибегнуть к геометрической интерпретации: при х—►— оо правая граница бесконечного квадранта (рис. 13) неограниченно сдвигается влево и при этом вероятность попадания слу­чайной точки в квадрант стремится к нулю.

2) Событие К< — оо невозможно, поэтому F (х, — оо) = 0.

3. Событие X < — оо и К< — оо невозможно, поэтому F(—оо, — оо) = 0.

4. Событие X < оо и Y < оо достоверно, следовательно, вероятность этого события F(oo, oo)=l.

Свойство становится наглядно ясным, если принять во внимание, что при х—► оо и у—>■ оо бесконечный кваД' рант (рис. 13) превращается во всю плоскость хОу ^и-следовательно, попадание случайной точки (X; У) в эту плоскость есть достоверное событие.

160

Свойство 4. а) При у = оо функция распределения

_аС(пемы становится функцией распределения составляю­сь „ у.

шеи л.

Fix oo) = F(x)

б) При х — оо функция распределения системы стано-_и(пся функцией распределения составляющей Y:

Доказательство, а) Так как событие К< оо досто­верно, то F (х, оо) определяет вероятность события X < х, _т е. представляет собой функцию распределения состав­ляющей X.

б) Доказывается аналогично.