§ 9. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс

Эмпирическим называют распределение относи­тельных частот. Эмпирические распределения изучает математическая статистика.

Теоретическим называют распределение вероятностей. Теоретические распределения изучает теория вероятностей. В этом параграфе рассматриваются теоретические распре­деления.

При изучении распределений, отличных от нормаль­ного, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характери­стики, в частности асимметрию и эксцесс. Для нормаль­ного распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предпо­ложить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса ука­зывают на значительное отклонение от нормального.

Как оценить асимметрию? Можно доказать, что для симметричного распределения (график такого распреде­ления симметричен относительно прямой х — М (X)) каждый Центральный момент нечетного порядка равен нулю. Для несимметричных распределений центральные моменты не­четного порядка отличны от нуля. Поэтому любой из этих моментов (кроме момента первого порядка, который равен Улю для любого распределения) может служить для ^Ценки асимметрии; естественно выбрать простейший из ^Их» т. е. момент третьего порядка \i₃. Однако принять ^Тот момент для оценки асимметрии неудобно потому, что

137

его величина зависит от единиц, в которых измеряется случайная величина. Чтобы устранить этот недостаток ц₃ делят на а³ и таким образом получают безразмерную характеристику.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

Асимметрия положительна, если «длинная часть» кри­ вой распределения расположена справа от математического *,_х, ожидания; асимметрия отри-

' ' ' Ас>0 цательна, если «длинная

а) """

ч асть» кривой расположена

слева от математического

М*(Х) ~х ожидания. Практически оп-

⁰ ределяют знак асимметрии

А_$<0

п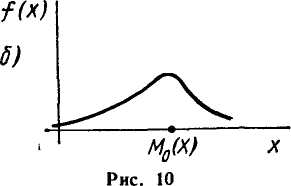 о расположению кривой рас­пределения относительно мо­ды (точки максимума диффе­ренциальной функции): если «длинная часть» кривой рас­положена правее моды, то асимметрия положительна (рис. 10, а), если слева — отрицательна (рис. 10, б).

а)

Нормальная ( —

Для оценки «крутости», т. е. большего или меньшего подъема кривой теоретического распределения по сравне­нию с нормальной кривой, пользуются характеристи­кой — эксцессом.

Э ксцессом теоретического распределения называют ха­рактеристику, которая опре­деляется равенством

Для нормального рас­пределения ц₄/°⁴ — 3; сле­довательно, эксцесс равен нулю. Поэтому если экс­цесс некоторого распре­деления отличен от нуля, то кривая этого распределе-

Рис. П

138

_иЯ отличается от нормальной кривой: если эксцесс ложительный, то кривая имеет более высокую и «острую» ^ершину, чем нормальная кривая (рис. 11, а); если эксцесс ^в_тр_Ицательный, то сравниваемая кривая имеет более низ-[ yjo и «плоскую» вершину, чем нормальная кривая /оис- 11» б)- При этом предполагается, что нормальное и Еретическое распределения имеют одинаковые матема­тические ожидания и дисперсии.