Методические указания.
1.Математическая формулировка прямой задачи.
2.Пример решения задачи линейного программирования на оптимальное использование ресурсов. Прямая задача.
Пусть предприятие производит 2 вида продуктов: печенье и бисквиты
Известен состав печенья и бисквитов
Известна прибыль от реализации единицы (1 кг) продукции
Известны запасы всех ресурсов
Известно, сколько каждого ресурса требуется на производство единицы (1 кг) каждого продукта
Составление модели начинается с введения переменных.
x1 - объем производства Печенья
x2 - объем производства Бисквитов.
Найти наилучший (оптимальный) производственный план – получить максимальную прибыль от реализации печенья и бисквитов.
……….
Все исходные данные представим в виде Таблицы:
|
Затраты ресурса на 1 кг продукта |
||
|
Печенье |
Бисквиты |
Доступный фонд ресурса |
|
X1 |
X2 |
Bj |
Выручка от 1 кг продукта ( Ci ) (руб.) – в строке |
32 |
27 |
|
Вид ресурса ( aij): |
|
|
|
Мука |
0,5 |
0,3 |
825 |
масло |
0,3 |
0,06 |
480 |
Яйца |
0,18 |
0,6 |
720 |
Сахар |
0,2 |
0,3 |
450 |
Труд |
0,07 |
0,09 |
200 |
оборуд по тесту |
0,015 |
0,006 |
40 |
оборуд.по выпечке-
|
0,0075 |
0,015 |
40 |
спрос/ печенье |
1 |
|
3000 |
Спрос/бисквиты |
|
1 |
3000 |
Дать математическую формулировку задачи:
Граничные условия представить в виде неравенств
Записать выражение для целевой функции
Граничные условия: Целевая функция:
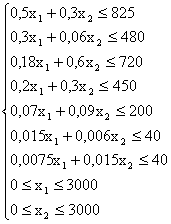
3.Двойственная задача.
1)Смысл двойственной задачи.
Предприятие 1 (П1), производящее продукцию, продаёт ресурсы Предприятию 2 (П2).
Цель П1:
Отражена в ограничениях двойственной задачи
Стоимость ресурсов, затрачиваемых на производство единицы продукции каждого вида, должна быть не меньше прибыли от реализации единицы продукции этого вида
i-е ограничение определяет стоимость всех ресурсов, которые нужно затратить на производство единицы i-го продукта:
кол. 1-го ресурса на единицу продукции *Цена 1-го ресурса + кол. 2-го ресурса единицу продукции * Цена 2-го ресурса +…>= прибыль от реализации единицы i-го продукта (руб/кг продукта)
Цель П2:
- Минимизировать суммарную стоимость ресурсов;
- Определяется целевой функцией:
запасы 1-го ресурса*Цена 1-го ресурса + запасы 2-го ресурса * Цена 2-го ресурса +… => min
2) Правила получения двойственной задачи из задачи исходной.
Если в исходной задаче ищется максимум целевой функции, то в двойственной ей - минимум.
Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.
В исходной ЗЛП все функциональные ограничения - неравенства вида “≤”, а в задаче, двойственной ей, - неравенства вида “≥”.
Коэффициенты при переменных в системах ограничений взаимно двойственных задач описываются матрицами, транспонированными относительно друг друга.
Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой.
Условие неотрицательности переменных сохраняется в обеих задачах.
