Московский авиационный институт

(национальный исследовательский университет)

Расчет точности операционных размеров путем решения технологической размерной цепи

Отчет по работе №3

Вариант 8

Выполнила студентка группы 03-409

Приходько А.Г.

Консультант доц. Грачев В.В.

Москва, 2012

1. Название и цель работы

Расчёт геометрических параметров паяльных трафаретов и экспериментальное исследование паяных соединений при монтаже поверхностно монтируемых компонентов электронных модулей

Цель работы – практическое освоение методики расчета требуемой точности операционных размеров при проектировании технологических процессов механической обработки путем построения и решения размерных цепей методами максимума-минимума и вероятностным методом, а также сопоставление этих методов по результатам расчета точности операционных размеров.

2. Общие сведения.

Основные ссылки на используемые источники информации:

1. файл «рам. цепи описание»

Основные сведения, используемые в работе:

В общем случае размерной цепью называется совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи. Технологические размерные цепи позволяют решать задачи обеспечения точности при изготовлении изделий.

Размерная цепь состоит из замыкающего и составляющих звеньев. По характеру влияния на замыкающее звено составляющие звенья разделяются на увеличивающие и уменьшающие. В зависимости от того, какие звенья цепи являются известными, и какие требуется определить, различают прямую и обратную задачи.

Прямая задача является проектной. При ее решении исходят из заданных требований к величине замыкающего звена, которые установлены заранее на основании аналитических расчетов, экспериментальных данных и нормативов. При этом определяются номинальные размеры, величины и координаты середин полей допусков, а также предельные отклонения всех составляющих размерную цепь звеньев.

При решении обратной задачи, на основании известных составляющих звеньев и их допусков, определяют номинальный размер, величину и координату середины поля рассеивания и предельные отклонения замыкающего звена. Необходимость ее решения возникает при анализе разработанного технологического процесса или спроектированной конструкции. Обратная задача может решаться в дополнение к прямой для проверки и правильности выполняемого решения, а также как самостоятельная задача в случае необходимости проверки принятых без расчета (например, по конструктивным или технологическим соображениям) размеров и допусков.

Построение технологической размерной цепи осуществляется на основе технологического процесса обработки детали. При этом используется чертеж или эскиз детали, где имеются размеры с допусками, участвующие в решении поставленной задачи, и операционные размеры в порядке их получения при обработке, начиная с размеров заготовки и кончая размерами обработанной детали.

Построение размерной цепи начинается с определения замыкающего звена. В данной работе замыкающее звено установлено заданием. Требуемая точность его регламентируется допуском. Графически отобразив замыкающее звено, последовательно пристраивают к нему составляющие звенья, участвующие в решении поставленной задачи, до тех пор, пока цепь не станет замкнутой.

Номинальные размеры замыкающего и составляющих звеньев (всего m) связаны между собой уравнением:

Для линейных размерных цепей с параллельными звеньями для увеличивающих составляющих звеньев размер берется со знаком “плюс”, а для уменьшающих – со знаком “минус”.

Допуск замыкающего звена определяется в зависимости от метода расчета.

При расчете на максимум-минимум:

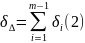
При расчете по вероятностному методу:

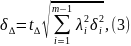
где 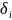– допуск составляющих звеньев;

– относительное среднее квадратическое отклонение;

–коэффициент, зависящий от принятого процента риска (брака) и закона распределения.

При нормальном законе распределения (Гаусса) и совпадении центра группирования с координатой середины поля допуска величина коэффициента выбирается из следующего ряда:

Процент риска (брака)	P, %	32	10	4,5	1,00	0,27	0,1	0,01
Коэффициент		1,00	1,65	2,00	2,57	3,00	3,29	3,89

Относительное среднее квадратическое отклонение =2 / ,

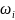где – среднее квадратическое отклонение;

– поле рассеивания размеров i-ого звена.

Для закона нормального распределения Гаусса (для крупносерийного и массового производства) =1/9. При других законах распределения коэффициенты и следует выбирать по табл. 1 с учетом количества составляющих звеньев размерной цепи.

Таблица 1. Значения коэффициентов и

Закон распределения отклонений		при числе составляющих звеньев
		2	3	4	5	6	>6
Симпсона (распределение по треугольнику)	1/6	2,80	2,83	2,86	2,88	2,91	3
Равной вероятности	1/3	2,45	2,55	2,61	2,65	2,68	3

При числе составляющих звеньев больше шести независимо от закона распределения с достаточной степенью точности можно принять =3. Если о законе распределения звена ничего неизвестно (для изделий мелкосерийного и единичного производства), то принимается закон равной вероятности.

Средняя величина допуска 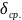составляющих звеньев при решении прямой задачи определяется по следующим ниже формулам.

При расчете на максимум-минимум (для линейных цепей с параллельными звеньями):

При вероятностном методе расчета:

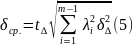
Допуск одного из составляющих звеньев 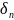при условии, что допуски остальных звеньев размерной цепи известны или определены ранее, вычисляется по формулам:

при расчете на максимум-минимум:

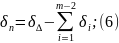
при вероятностном методе расчета:

где n – номер искомого звена.

Расположение полей допусков относительно номинальных значений звеньев и предельные отклонения определяются независимо от метода расчета размерной цепи.

Координата середины поля допуска замыкающего звена связана с координатами середин полей допусков составляющих звеньев следующими уравнениями:

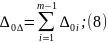
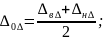
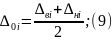
где 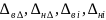–верхнее и нижнее отклонения замыкающего и составляющего звеньев.

При решении прямой задачи известной обычно является координата середины поля допуска только замыкающего звена. Поэтому координаты середин полей допусков всех составляющих звеньев принимаются по конструктивным или технологическим соображениям, за исключением какого-либо одного звена, координата середины поля допуска которого определяется затем по уравнению (8).

Предельные отклонения любого звена размерной цепи определяются по формулам:

;

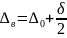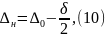
Где – верхние и нижние предельные отклонения звена размерной цепи;

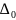– координата середины поля допуска звена;

δ – допуск звена.