5 Основы построения страховых тарифов по страхованию жизни

Основные положения методологии расчета тарифов

 Страховой тариф, как нами отмечено ранее, представляет собой сумму денег, которую уплачивает страховщику за страхование каждый страхователь с единицы страховой суммы или предмета страхования и тем самым каждый страхователь участвует в создании страхового фонда страховщика по данное виду страхования.

Задача правильного построения страхового тарифа по любому виду страхования заключается в том, чтобы сформировать за счет нетто-ставки тарифа фонд денежных средств, достаточный для страховых выплат по страховым случаям за расчетный (тарифный) период.

Расчет страховых, тарифов по всем видам страхования жизни имеет определенные особенности, связанные с предметом страхования.

Этим предметом страхования является жизнь человека, постоянно подвергающегося различным опасностям, последствиями которых может быть и смерть застрахованного.

Поэтому страхование жизни предусматривает страховую защиту имущественных интересов застрахованного лица (его выгодоприобретателей) путем страховых выплат при его дожитии до определенного возраста (или окончания срока страхования), а также в случае его смерти.

Вероятность дожить до определенного возраста или окончания срока страхования зависит в первую очередь от возраста в момент страхования и срока действия договора страхования жизни.

На основании массовых данных демографической статистики и теории вероятностей выявлена подчиняющаяся закону больших чисел зависимость смертности от возраста людей, выведены соответствующие математические формулы для расчета.

По специально разработанной методике с применением этих формул составляются таблицы смертности.

Пример формы таблицы смертности и средней продолжительности жизни

(извлечение)

Возраст лет (X)	Число доживающих из 100000 родившихся до возраста хлет ( lx)	Число умирающих при переходе от возраста х к возрастух + 1 лет ( dx)	Вероятность умереть в течение предстоящего года жизни (qx)	Средняя продолжительность предстоящей жизни (ех)
О	100000	2462	0,24620	68,49
1 … …	97538	327	0,00336	69,21
18 …	96264	93	0,00097	53,05
20 …	96064	119	0,00124	51,15
40	91 366	406	0,00445	33,17
41	90960	429	0,00472	32,32
42	90531	458	0,00506	31,47
43	90073	493	0,00547	30,62
44	89580	533	0,00595	29,79
45 …	89047	576	0,00647	28,96
50 …	85 745	778	0,00908	24,98
60 …	75 902	1 297	0,01708	17,92
85	16 295	2368	0,14535	4,89

Таблицы периодически пересчитываются в связи с изменением показателей смертности населения. Они содержат конкретные цифры смертности для каждого возраста (в полных годах) для 100 000 населения с последовательным уменьшением доживающих при переходе от одной возрастной группы в другую группу, имеющую возраст больше на 1 год.

 По таблицам смертности вероятность умереть в возрастеХ -лет, не дожив до возрастах + 1 год, определяется по формуле

q _х = d_x / l_x .

Вероятность дожить до любого возраста р_х - определяется как разность между 1,0 иq_x , т.е.

р_х = 1 - q_x .

Достоверность и математическая точность данных таблиц смертности позволяют использовать их для финансовых расчетов, включая расчет нетто-ставки по видам страхования жизни.

Только используя таблицы смертности, можно рассчитать, какой величины страховой фонд, например, по страхованию жизни «на дожитие» необходимо иметь страховщику к определенному моменту, учитывая разные возрасты застрахованных лиц и сроки страхования по совокупности договоров страхования.

Зная требуемую величину страхового фонда для страховых выплат, количество доживающих до данного момента застрахованных лиц, доходность от инвестирования страховых резервов по страхованию жизни, можно рассчитать нетто-ставку на дожитие.

Расчеты нетто-ставки весьма сложны, так как требуют учета не только возраста застрахованных лиц, но и порядка, сроков и периодичности уплаты страховых премий (взносов), нормы доходности инвестиций, а также размеров, периодичности и продолжительности страховых выплат.

Синтез и развитие математических методов, применяемых в статистике, теории вероятностей и долгосрочных финансовых расчетов сформировали особую отрасль науки в области страхования — теорию актуарных расчетов.

На основе теории актуарных расчетов разрабатываются страховые тарифы по страхованию жизни.

В настоящее время к актуарным расчетам относятся также теоретические и методические основы расчета страховых тарифов по другим подотраслям личного страхования и по имущественным видам страхования.

Теоретические, методические основы и примеры расчетов страховых тарифов по видам страхования жизни освещаются в книгах, учебниках ряда авторов.

В настоящем учебном пособии ставится задача изложения в краткой форме основ построения страховых тарифов по страхованию жизни.

Страховые тарифы по всем видам личного устанавливаются на основе рассчитанной нетто-ставки и величины нагрузки.

Особенность расчетов тарифных ставок по видам страхования жизни заключается в том, что в них, как правило, учитываются доходы от инвестирования страховых резервов, уменьшающие размер страховых тарифов.

В расчетах тарифных ставок по всем видам страхования жизни возникает необходимость получения ответа на вопрос: каким должен быть размер уплачиваемой страхователем страховой премии (взноса) в начале страхового периода для того, чтобы через п лет срока страхования при определенном порядке внесения страховых платежей, норме доходности (норме годового процента) инвестирования страховых резервовзастрахованный (выгодоприобретатель) получил страховую выплату (страховую сумму)B_n ?

Ответ на этот вопрос при единовременной уплате страховой премии можно получить из расчета увеличения банковского вклада при начислении дохода по сложным процентам.

Например, сумма банковского вклада равна А, годовой процент по вкладу (допустим, постоянный) - i , срок вклада по договору -п лет.

По годам сумма А будет увеличиваться и формировать промежуточные значения конечной накапливаемой суммы вклада с начисленными процентами зап лет-B_n ,в частности:

- за первый год	В1 = А (1 + i) ;
- за второй год	B2 = В1 (1 + i) = А (1 + i)(1 + i) = А (1 + i)2 ;
- за третий год	B3 =B2( 1 + i)=A(1 +i)2(1 + i) = A(1 + i)3 ;
- за n-й год	Bn = А (1+ i)п .

Страховые резервы страховщики размещают не только в банковские вклады, поэтому этот принцип нарастания первоначальных сумм, полученных страховыми компаниями по страхованию жизни, применяется в расчетах и для других направлений инвестирования средств.

Величина (1+ і) называется процентным множителем. За п лет он составит величину (1+ i ) ⁿ.

Исходя из выявленной зависимости формирования фонда денежных средств от нормы доходности и срока инвестирования страховых резервов по страхованию жизни, можно вывести формулу для определения величины уплачиваемой страховой нетто-премии в начале страхования А:

А = В _.

С целью упрощения расчетов формула преобразуется заменой сомножителя в виде дроби на дисконтирующий множитель (дисконт) V :

V = .

Возведенный в степень п, он будет дисконтом (дисконтирующим множителем) зап лет :

Vⁿ= ( 1 )

 Дисконтирующий множитель определяет, какую долю от величины фонда денежных средств, предусмотренного к получению от страховщика в виде страховых выплат через - п лет при норме доходности инвестиций -і , необходимо уплатить страхователю в форме страховой нетто-премии сегодня, в начале страхования.

Дисконт в относительной величине — по отношению к фонду денежных средств, планируемому к выплате, — устанавливает современную стоимость этого фонда средств.

Основные положения методики расчета нетто- и брутто-ставки по страхованию на дожитие и на случай смерти

Тарифные ставки рассчитываются для различных способов уплаты страховой премии по страхованию жизни.

Страховая премия может уплачиваться единовременно или путем внесения страховых взносов с определенной договором страхования жизни периодичностью (один раз в год ежеквартально или ежемесячно в течение установленного периода времени либо всего срока страхования).

С позиций концентрации денежных ресурсов, продолжительности и эффективности инвестирования страховых резервов, увеличения дохода для страховщика значительно выгоднее единовременная уплата страховой премии.

Кроме того, единовременная уплата страхователем страховой премии более надежна для страховщика, так как какие-либо непредвиденные обстоятельства в жизни или деятельности страхователя в этом случае не отразятся на выполнении им этого обязательства перед страховщиком. Уменьшаются также расходы на сбор, учет страховой премии, банковские операции с денежными средствами страховой организации.

Для большинства страхователей, наоборот, предпочтительнее уплата страховой премии частями (взносами) в течение длительного периода времени.

Поэтому обычно в правилах страхования жизни страховщики предусматривают различные способы уплаты страховой премии.

Рассмотрим на примере основные положения метода определения единовременных нетто- и брутто-ставок по страхованию на дожитие и на случай смерти при следующих исходных данных:

•  возраст страхования (полных лет) на момент заключения договора страхования, х = 40 лет;

•  количествоподлежащих страхованию лиц по таблице смертности (достигших возрастах = 40 лет из100 000 родившихся) для принятого возраста страхования L_x = 91 366 человек;

•  срок страхования п= 5 лет;

•  число лиц, доживающих до окончания срока страхования, по таблице смертностиL_{x + n} = 89 047 человек;

•  норма доходности инвестирования страховых резервов i = 0,07;

•  единица измерения страховой суммы, на которую рассчитывается тарифная ставка и которая условно принята в примере расчета тарифа в качестве страховой суммы по договору страхования жизни каждого застрахованногоS = 100 грн.

Рассчитаем сначала единовременную нетто-ставку для договоров страхования на дожитие.

Через 5 лет страховщик должен иметь определенную величину фонда денежных средств ( B ₅ ) , сформированную за счет страховых взносов (страховой премии), уплачиваемых единовременно страхователями, и инвестиционного дохода.

Сумма фонда должна быть достаточной для выплаты страховой суммы S , равной 100 руб., всем дожившим до окончаний срока страхования и достигшим45-летнего возраста, т.е.

B ₅ = L₄₅ S = 89 047 • 100 = 8 904 700 грн.

Однако в начале страхования общая уплачиваемая страхователями сумма страховой нетто-премии может быть меньше, так как в течение 5 лет она будет возрастать (вместе с начисленным доходом за каждый год) ежегодно на 7 сложных процентов за счет инвестирования страховых резервов по страхованию жизни.

Поэтому современная стоимость (на начало страхования) требующегося фонда денежных средств ( A_x ) может быть рассчитана по формулес использованием дисконтирующего множителяVⁿ:

A_x = B_n • Vⁿ = B ₅ • V ⁵ = 8 962 грн.

Такая сумма — 6 348 963 грн. — должна быть получена страховщиком в виде уплаченной страхователями страховой нетто-премии для обеспечения выплат страховых сумм в размере 100 грн. через 5 лет всем дожившим до окончания срока страхования и возраста 45 лет застрахованным в 40-летнем возрасте лицам.

Для того чтобы определить, какую сумму нетто-премии должен заплатить каждый страхователь, необходимо разделить A_x на количество вступивших в страхование лиц L_x = 91 366 человек.

Это и будет единовременная нетто-ставка( _n E_x ) по страхованию на дожитие со 100 грн., страховой суммы для возрастах = 40 лет при сроке страхования п = 5 лет и норме доходностиi = 0,07.

В результате преобразований формула для расчета

единовременной нетто-ставки на дожитие с 1 гривни страховой суммы( _n E_x ) будет иметь следующий вид:

_n E_x = . ( 2 )

Анализируя выведенную формулу, можно сделать два вывода:

• чем длительнее срок страхования на дожитие, тем ниже нетто-ставка, так как увеличивается сумма учитываемого в расчете и снижающего нетто-ставку дохода от инвестируемых страховых резервов по страхованию жизни;

• нетто-ставка выше для меньшего возраста застрахованных лиц в сравнении с нетто-ставкой для лиц большего возраста при одинаковом сроке страхования на дожитие, так как среди более молодых ниже смертность.

Проводя аналогичные рассуждения,рассчитаем единовременную нетто-ставку по страхованию на случай смерти по тем же исходным данным и числу умирающих в каждом году страхования из таблицы смертности.

Общая величина необходимого фонда денежных средств В _n для выплаты страховых сумм S в размере 100 руб. по случаю смерти застрахованных лиц всем их выгодоприобретателям, начиная с первого и до последнего года страхования ,может рассчитываться по формуле

,

где d _х , d_{x +1} , d_{x +2}, ...d_{x + n -1} - число умирающих по срокам страхования в годах.

Современная стоимость (на начало страхования) необходимого фонда денежных средств (А_х) рассчитывается с учетом дисконтирующего множителя по формуле

.

Для определения единовременной нетто-ставки по страхованию на случай смерти (_пА_х)с 100 грн. страховой суммы необходимо A_x разделить на число вступивших в страхование лиц L_x, т.е.

.

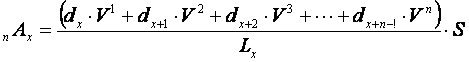Окончательная рабочая формула для расчетаединовременной нетто-ставки на случай смерти с 1 гривни страховой суммы( _n А_х ) будет иметь следующий вид:

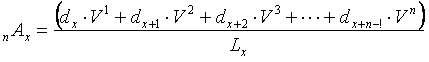 . (3)

Брутто-ставка( Т_б ) при страховании рассчитывается по формуле

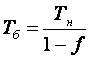(4)

гдеТ_н - соответствующая единовременная нетто-ставка по виду страхования ;

f= К_вд + К_пр - удельный вес нагрузки в структуре брутто-ставки:

К_вд - норматив расходов на ведение дела;;

К_пр -норматив прибыли .

Формулы для расчета норматива расходов на ведение дела( К_вд ) и норматива прибыли ( К_пр ) нами были представлены ранее в теме «Актуарные расчеты в страховании ».

Переход от единовременной нетто-ставки к ставке при уплате страховой премии в рассрочку

В случае уплаты страховых взносов ежегодно в течение установленного договором страхования периода для всего срока страхования жизни страховщик не может получить такой же доход от инвестирования страховых резервов, как при единовременной уплате страховой премии.

Кроме того, часть взносов страховщик вообще не получит из-за уменьшения числа застрахованных лиц вследствие их смертности.

Поэтому нетто-ставку при рассрочке страховых платежей нельзя определять простым делением единовременной нетто-ставки на число лет страхования.

Чтобы обеспечить получение страховой премии при рассрочке ее уплаты по годам страхования в сумме, эквивалентной (с компенсацией потерь части доходов от инвестирования средств резервов и страховых взносов), но не равной арифметически уплачиваемой единовременно страховой премии,рассчитываются годичные нетто-ставки .

Годичные нетто-ставки исчисляются делением единовременных нетто-ставок на коэффициенты рассрочки.

Значения коэффициентов рассрочки всегда несколько меньше числа лет (срока) страхования.

Поэтому полученные с помощью коэффициентов рассрочки годичные нетто-ставки взносов по величине больше, чем их значения, получаемые простым делением единовременных нетто-ставок на количество лет страхования.

За счет такого различия в величине годичных и единовременных нетто-ставок компенсируются потери страховщика в связи с рассрочкой уплаты страховой премии в сравнении с единовременным страховым платежом.

Применяются два вида коэффициента рассрочки в зависимости от времени уплаты годовой суммы страхового взноса:

• коэффициент рассрочки постнумерандо — при уплате взноса в конце года;

• коэффициент рассрочки пренумерандо — при уплате взноса в начале страхового года.

Формула для расчета, например коэффициента рассрочки постнумерандо, выводится путем использования следующего алгоритма расчета и математических зависимостей между рассматриваемыми в примере показателями:

1 Допускается, что к концу каждого года страхования все страхователи уплачивают страховой взнос в размере 1 грн.

2 Общая сумма уплаченных взносов в конце каждого года страхованияопределяется умножениемчисла доживших(по таблице смертности) до возрастной группы следующего года L_{x +1} на 1 грн. годового взноса.

Например, для первого года страхования общая величина уплаченных страховых взносов равна L_x+1 . 1.0 = L_{x+1 .}

Для второго года- L_{x +2} .

Для n -гогода L_{x+ n} .

3 Современная стоимость общей суммы уплаченных всеми страхователями в конце первого страхового года взносов определяется умножением суммы взносов - L _х+1 на дисконтирующий множитель - V,

т.е.L _х+1 • V .

Современная стоимость взносов второго года будет равна - L _х+2 • V ², а n -го года — L_{х+ n} • Vⁿ .

4 Для каждого из вступивших в страхование лицL _х величина современной стоимости общей суммы годичных взносов за срок страхования n лет с уплатой их в конце каждого страхового года ( _па'_х ) определяется по формуле ( коэффициент рассрочки платежа постнумерандо ):

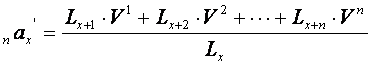, (5)

где_п а'_х -представляет собой современную стоимость годичной ставки взноса в размере 1 грн. при сроке страхования п лет и норме доходности - i .

Аналогично выводится формула современной стоимости общей суммы годичных взносов за п лет с уплатой их в начале года в расчете на одного страхователя ( коэффициент рассрочки платежа пренумерандо ):

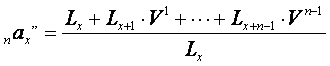. (6)

Таким образом, использование коэффициентов рассрочки платежа позволяет страховщику рассчитать годовые нетто-ставки,т.е. единовременные ставки, рассчитанные по формулам ( 2 ) и( 3 ), делятся на коэффициенты рассрочки платежа, которые определяются по формулам( 5 ) и ( 6 ).

В практике страхованияпри расчетах годовых нетто-ставок на дожитие и на случай смерти, как правило, используется коэффициент рассрочки платежа пренумерандо.

В случае уплаты ежемесячных платежей рассчитываются соответствующие месячные ставки путем деления годовых нетто-ставок на число 12.

 

 Брутто-ставка( Т_б ) при расчетах годовых и месячных платежейрассчитывается по формуле

гдеТ_н - соответствующая годовая или месячная нетто-ставка по виду страхования ;

f= К_вд + К_пр - удельный вес нагрузки в структуре брутто-ставки;

 К_вд - норматив расходов на ведение дела;

К_пр -норматив прибыли .

Основные положения методики расчета нетто- и брутто-ставок по страхованию ренты и пенсии

Формулы для расчета нетто-ставок по страхованию пожизненной ренты и пожизненной пенсии выводятся практически одинаково.

Предположим, что договоры страхования пожизненной ренты (пенсии) заключают все лица, достигшие возрастах лет, т.е. по таблице смертности L_xчеловек.

Размер годовой ренты (пенсии) для установления нетто-ставки со 100 грн. страховой суммы принимаем условно 100 грн. ( S = 100 грн.).

 Начало выплаты ренты (пенсии) черезп полных лет.

Число доживших до получения ренты (пенсии) лиц через п лет будет равно L_х+п .

Расчеты единовременных нетто-ставок пост- и пренумерандо производятся соответственно по формулам.

Единовременная нетто-ставка постнумерандо

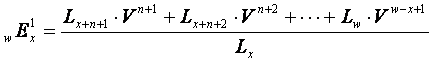. (7)

Единовременная нетто-ставка пренумерандо

. (8 )

Переход от единовременных нетто-ставок к годичным и месячнымнетто-ставкам осуществляется путем деления единовременных ставок накоэффициенты рассрочки и число 12 .

Формулы для расчета коэффициентов рассрочки пост- и пренумерандо будут иметь следующий вид:

- коэффициент рассрочки постнумерандо

;(9)

- коэффициент рассрочки платежа пренумерандо

. (10)

Брутто-ставка( Т_б ) при расчетах годовых и месячных платежейрассчитывается по формуле:

гдеТ_н - соответствующая годовая или месячная нетто-ставка по виду страхования;

f= К_вд + К_пр - удельный вес нагрузки в структуре брутто-ставки;

 К_вд - норматив расходов на ведение дела;

К_пр -норматив прибыли .

В последние годы математический аппарат расчета страховых тарифов получил значительное развитие. Выведены формулы для расчета тарифных ставок на персональных компьютерах.

Разработанные страховые тарифы в стабильных экономических условиях действуют обычно продолжительное время и являются важнейшим элементом в организации экономических отношений между страхователями и страховщиком.

Умножением тарифной брутто-ставки на страховую сумму определяется размер страховой премии, уплачиваемой страхователем за страхование страховщику.

Своевременная уплата страхователем страховой премии (взносов) является основным его обязательством перед страховой организацией.