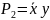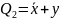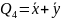6.6 Аналитическое представление логических функций.

Рассмотренное выше представление логических функций наглядно и может быть применено для функций от любого количества переменных, однако такая запись не является компактной при анализе свойств функций алгебры логики . Проще выглядит аналитическая запись в виде формул. Но наиболее рациональным является представление логических функций в так называемых нормальных формах. Основу этих формул составляют понятия элементарных конъюнкций и дизъюнкций.

Элементарная конъюнкция (минтерм) образуется конъюнкцией конечного множества логических переменных и их инверсий, например:

Элементарная дизъюнкция (макстерм) образуется дизъюнкцией конечного множества логических переменных и их инверсий, например:

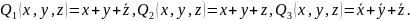
Элементарная конъюнкция принимает единичное значение только при одном из всех возможных наборов входных переменных, а элементарная дизъюнкция принимает нулевое значение только при одном из возможных наборов аргументов и единичное значение при всех других.

Следовательно, минтерм алгебраически представляет собой конъюнкцию аргументов и их инверсий, а макстерм – дизъюнкцию аргументов и их инверсий.

Количество минтермов и макстермов совпадает с количеством возможных наборов аргументов. В таблице 6.2. приведены значения элементарных конъюнкций и дизъюнкций для двух аргументов.

Таблица 6.2. Элементарные конъюнкции и дизъюнкции двух переменных

Значения аргументов		Значения элементарных конъюнкций				Значения элементарных дизъюнкций
X	Y
0	0	0	0	0	1		0	1	1	1
0	1	0	1	0	0		1	1	0	1
1	0	0	0	1	0		1	0	1	1
1	1	1	0	0	0		1	1	1	0

Количество аргументов, образующих элементарную конъюнкцию или дизъюнкцию называется ее рангом. Например, ранг минтерма равен 3.

Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.

Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.

Т.е. нормальная форма – это объединение термов, включающее минтермы переменного ранга.

Количество всех термов, входящих в состав ДНФ равно количеству единичных строк таблицы истинности заданной функции.

Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции (макстермы), связанные между собой операцией конъюнкции.

1. Совершенные нормальные формы.

Одну и ту же логическую функцию можно представить различными ДНФ и КНФ. Из всей совокупности нормальных форм выделяют одну ДНФ и одну КНФ, а именно такие формы, которые являются инверсными по отношению друг к другу, т.е. если одна из них равна «1», то другая при этом равна «0», и наоборот. Эти формы называются совершенными нормальными формами.

Дизъюнктивная совершенная нормальная форма (СДНФ) отвечает следующим требованиям:

• в ней нет двух одинаковых элементарных конъюнкций;

• ни одна конъюнкция в ней не содержит одинаковых переменных;

• ни одна конъюнкция не содержит двоичную переменную с ее инверсией;

• все конъюнкции являются элементарными;

• все конъюнкции имеют одинаковый ранг.

Для представления функции в СДНФ может быть использована также операция .

Сформулируем требования, которые предъявляются к операции связывающей элементарные минтермы:

1. Если какой-либо терм 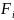= 1, то функция должна быть равна 1.

2. Если какой-либо терм = 0, то функция может быть равна 1.

3. Необходимо, чтобы при значениях термов = 0 функция была равна нулю.

Табличное представление операций отвечающих требованиям имеет вид, представленный в таблицах 6.3. и 6.4.3:

Таблица 6.3. Таблица6.4.

		=+
0	0	0
0	1	1
1	0	1
1	1	1

		=
0	0	0
0	1	1
1	0	1
1	1	0

Любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме:

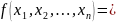
, где

- элементарный минтерм; знак  обозначает операции +, ;

k – количество наборов, на которых функция равна 1.

Конъюнктивная совершенная нормальная форма (КСНФ) отвечает следующим требованиям:

• в ней нет двух одинаковых элементарных дизъюнкций;

• ни одна дизъюнкция в ней не содержит двух одинаковых переменных;

• ни одна дизъюнкция не содержит переменную вместе с ее инверсией;

• все дизъюнкции имеют один и тот же ранг.

Чтобы определить, какие операции могут связывать элементарные дизъюнкции, изложим следующие требования:

1. Если какой-либо терм = 0, то функция должна быть равна 0.

2. Если все термы = 0, то функция равна 1.

Выполняя эти требования можно привести к операциям конъюнкции и равнозначности (таблица 6.5. и 6.6):

Таблица 6.5. Таблица 6.6.

		
0	0	0
0	1	0
1	0	0
1	1	1

		
0	0	1
0	1	0
1	0	0
1	1	1

Вывод: любая таблично заданная ФАЛ может быть задана в аналитической форме:

, где

знак  обозначает операции  и , k – количество двоичных наборов, для которых =0.

В алгебре логики строго доказывается, что любая логическая функция, кроме , представима в ДСНФ, любая функция, кроме , представима в КСНФ.

Формулы в ДСНФ или КСНФ можно получить по табличному представлению логической функции.

Для образования ДСНФ необходимо выполнить следующие действия:

1. по каждому набору двоичных переменных, при котором логическая функция принимает значение 1, составить элементарные конъюнкции;

2. в элементарные конъюнкции записать без инверсии переменные, заданные единицей в соответствующем наборе, и с инверсией – переменные заданные нулем;

3. соединить элементарные конъюнкции знаком операции дизъюнкции или операции сложение по модулю 2.

Для образования КСНФ необходимо выполнить аналогичную последовательность действий:

1. по каждому набору двоичных переменных, при котором логическая функция принимает значение 0, составить элементарные дизъюнкции;

2. в элементарные дизъюнкции записать без изменения переменные, заданные нулем в соответствующем наборе, и с инверсией – переменные заданные единицей;

3. соединить элементарные дизъюнкции знаком конъюнкции.

Пример.

Пусть задана некоторая функция (см таблицу 6)

Получим для заданной функции СДНФ и СКНФ.

Функция принимает значение 1 для четырех наборов и значение 0 для других четырех наборов.

Значения аргументов			Значения функции	ДСНФ		КСНФ
X	Y	z
0	0	0	1		-
0	0	1	0	-
0	1	0	1		-
0	1	1	0	-
1	0	0	1		-
1	0	1	0	-
1	1	0	0	-
1	1	1	1	xyz	-

Функция в СДНФ состоит из логической суммы четырех элементарных конъюнкций третьего ранга:

Функция в СКНФ является логическим произведением четырех элементарных дизъюнкций третьего ранга:

Совершенная нормальная форма отличается от нормальной формы тем, что всегда содержит термы только максимального ранга и дает однозначное представление функции.

Произвольная нормальная дизъюнктивная форма переводится в СДНФ следующим образом:

пусть 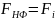, тогда

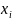, где - переменная, которая не входит в данный терм .

Пример.

Логическую функцию, заданную в ДНФ преобразовать в СДНФ.

.

Произвольная КНФ переводится в СКНФ логическим умножением дизъюнкции младшего ранга на конъюнкцию 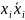, где – переменная, которая не входит в данный терм.

Пусть 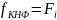, тогда

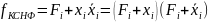
Пример.

При использовании аналитических форм представления обычно стремятся к упрощению логических функций.