Побудова кута, що дорівнює даному (див. Малюнок № 7.1.).

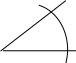
А М

В О

С К

Малюнок № 7.1.

Нехай нам слід побудувати кут, що дорівнює куту АВС. Якщо не вказаного вершину кута, який необхідно побудувати, то проводимо довільний промінь і на ньому позначаємо точку О. Довільним розхилом циркуля з центром в точці В проводимо дугу, яка перетинає сторони кута АВС. Цим же розхилом циркуля проводимо дугу з центром в точці О. Нехай промінь перетинається з цією дугою в точці К. Вимірюємо циркулем розхил АС і з центром в точці К проводимо дугу до перетину в точці М з іншою дугою. Проводимо промінь ОМ. Отримали МОК= АВС.

Поділ відрізка пополам.

Нехай нам задано відрізок АВ, який потрібно поділити на дві рівні частини. Розхилом циркуля, більшим за половину відрізка АВ, проводимо дві дуги з центрами в кінцях відрізка. Нехай вони перетнулися в точках С і Д. Через ці точки проводимо пряму, яка перетне заданий відрізок АВ у точці О, яка і буде серединою заданого відрізка (див. мал. № 7.2.).

С

А О В

Д

Малюнок № 7.2. Поділ кута пополам.

Нехай задано кут АВС, який необхідно поділити навпіл. Проводимо довільним розхилом циркуля дугу кола з центром в точці В, яка перетинає сторони кута в точках А і С. Проводимо розхилом циркуля, більшим за половину дуги АС, дві дуги з центрами в точках А і С. Нехай точка їх перетину буде Д. Проводимо промінь ВД, який поділяє кут АВС навпіл (див. мал. № 7.3.).

А

Д

В

С

Малюнок № 7.3.

Побудова прямої, яка проходить через дану на ній точку, перпендикулярно до даної прямої (малюнок № 7.4.).

К

А С В

Малюнок № 7.4.

Нехай нам задано деяку пряму АВ, на якій позначено точку С. Потрібно побудувати пряму, яка б проходила через точку С, перпендикулярно до прямої АВ. Довільним розхилом циркуля з центром в точці С робимо дві засічки. Одержали відрізок, кий необхідно поділити пополам. Побудувавши пряму КС, ми отримаємо пряму, яка проходить через точку С перпендикулярно до прямої АВ (див. мал. № 7.4.).

Побудова трикутника за трьома сторонами.

Нехай нам задано три відрізка a, b, c і необхідно побудувати трикутник, сторони якого б дорівнювали цим відрізкам. На довільній прямій МК відкладаємо відрізок, що дорівнює відрізку а. Нехай його кінцями будуть точки В і С. З центром в точці В розхилом циркуля, що дорівнює відрізку c, проводимо дугу. З центром в точці С розхилом циркуля, що дорівнює відрізку b, проводимо дугу. Нехай проведені дуги перетинаються в точці А. Проводимо відрізки АВ і АС. Тоді трикутник АВС буде шуканим (див. мал. № 7.5.). Зазначимо, що задача може не мати розв’язку, якщо сума відрізків двох відрізків менша, за третій відрізок.

а А

b

c

В С