Б. Электрохимические процессы в гальваническом элементе

Пример 5. Вычисление равновесных электродных потенциалов металлов и

газовых электродов

1. Вычислите потенциал цинкового электрода при 298К в 150 мл раствора, содержащего 1,2 г цинка сульфата ZnSO₄. Кажущаяся степень диссоциации соли в растворе равна 60%.

Решение. Вначале рассчитываем молярную концентрацию раствора цинка сульфата:

С_μ(ZnSO₄) = = = 0,0496 моль/л.

В данном примере молярная концентрация раствора цинка сульфата не совпадает с молярной концентрацией ионов Zn²⁺, т.к. кажущаяся степень диссоциации соли равна 0,6. Молярная концентрация ионов цинка в растворе составит:

С_μ(Zn²⁺) = a×C_μ(ZnSO₄) = 0,6∙0,0496=0,0298 (моль/л).

Потенциал цинкового электрода определяется уравнением Нернста (уравнение 9 теоретической части раздела):

j _Zn²⁺_{/ Zn} = j⁰ _Zn²⁺_{/ Zn} + ℓna(Zn²⁺).

В случае разбавленных растворов при вычислении электродного потенциала в уравнении Нернста вместо активности потенциалопределяющего иона можно использовать его молярную концентрацию. Учтем также и стандартные условия измерения электродного потенциала, тогда:

j _Zn²⁺_{/ Zn} = j⁰ _Zn²⁺_{/ Zn} + ℓgС_μ(Zn²⁺);

j _Zn²⁺_{/ Zn} = –0,763 + 0,0296∙ℓg0,0298 = –0,763 – (0,0296∙1,526) = 0,808 (В).

Значение стандартного электродного потенциала цинка j⁰ _Zn²⁺_/Zn взято из таблицы № 1 Приложения.

Ответ: j _Zn²⁺_{/ Zn} = 0,808 В.

2. Потенциал серебряного электрода, погруженного в насыщенный раствор соли серебра бромида при 298К, равен 0,435 В (относительно стандартного водородного электрода). Вычислите активность ионов серебра в растворе, если j⁰ _Аg⁺_{/ Ag} = 0,799 В.

Решение. Потенциал серебряного электрода определяется уравнением Нернста:

j_Ag⁺_{/ Ag} = j⁰ _Ag⁺_{/ Ag} + ℓna(Ag⁺) = 0,799 + 0,0591∙ℓga(Ag⁺),

откуда находим

ℓga(Ag⁺) = = -6,159 = -7+0,841;

a(Ag⁺) = 10^-7∙6,934 = 6,934∙10^-7.

Ответ: a(Ag⁺) = 6,934∙10^-7 моль/кг.

3. Рассчитайте равновесный потенциал хлорного газового электрода, на котором при температуре 298 К установилось равновесие:

Cl₂ + 2ē <=> 2Cl^–

при парциальном давлении газообразного хлора P̃(Cl₂) = 10 кПа и активности хлорид-ионов а(Cl^–) = 1∙10^-2 моль/кг.

Решение. Величина равновесного электродного потенциала электрохимической системы рассчитывается по уравнению Нернста, причем, для газообразного электрода оно имеет вид: φ_Cl2/2Cl^- = φ⁰_Cl2/2Cl^- + ℓn .

Решим это уравнение, предварительно найдя в Таблице № 1 Приложения значение стандартного электродного потенциала хлора φ⁰_Cl2/2Cl^- = 1,39 В:

φ_Cl2/2Cl^- = 1,39 + ℓg = 1,39 + = 1,39 + 0,177 = 1,567 В.

Ответ: φ_Cl2/2Cl^- = 1,567 В.

4. Рассчитайте равновесный потенциал стандартного водородного электрода, погруженного при температуре 298 К в кислотный раствор с рН, равным 3,5.

Решение. Для измерения рН водных растворов используют в качестве электрода сравнения стандартный водородный электрод Н₂|2Н⁺, потенциал которого при стандартных условиях φ⁰_Н2|2Н+ (Т = 298 К, Р = 101 кПа) принят равным нулю. Если активность ионов водорода в исследуемом растворе отлична от 1 моль/кг, то значение равновесного электродного потенциала водородного электрода можно определить по уравнению Нернста:

φ_Н2|2Н+ = φ⁰_Н2|2Н+ + ℓn .

В этом уравнении:

φ⁰_Н2|2Н+ = 0, сомножитель RT∙2,303/F = 0,0591, N_ē = 2 (2H⁺ + 2ē = H₂) и тогда

φ_Н2|2Н+ = ℓga²(Н⁺).

Из уравнения рН = - ℓga(Н⁺) найдем ℓga(Н⁺) = - рН = -3,5 = -4 + 0,5, следовательно, а(Н⁺) = 10^-4∙3,16 = 0,3∙10^-3 (моль/кг).

Теперь решим уравнение Нернста: φ_Н2|2Н+ = 0,0295∙ℓg(0,3∙10^-3)² = -0,208 (В).

Ответ: φ_Н2|2Н+ = -0,208 В.

5. Определите, при какой концентрации (моль/кг) ионов Fe²⁺ потенциал железного электрода φ_Fe|Fe2+ при стандартных условиях станет на 0,015 В меньше его стандартного электродного потенциала. Коэффициент активности ионов железа Fe²⁺ равен 0,752.

Решение. Потенциал железного электрода для равновесного процесса Fe - 2ē <=> Fe²⁺ определяется по уравнению Нернста

φ_Fe|Fe2+ = φ⁰_Fe|Fe2+ + ℓn .

Поскольку величина стандартного железного электрода, согласно Таблице № 1 Приложения, равна 0,44 В, то уменьшение величины потенциала на 0,015 В приходится на второе слагаемое в указанной формуле, следовательно,

ℓn = -0,015.

Решим это уравнение, имея в виду, что при стандартных условиях сомножитель RT∙2,303/F = 0,0591, N_e = 2, и тогда

ℓg a(Fe²⁺) =- = -0,508 = -1 + 0,492; a(Fe²⁺) = 10^-1∙3,1 = 0,31 (моль/кг).

Зная, что активность ионов в растворе равна произведению коэффициента активности на моляльную концентрацию, несложно рассчитать теперь искомую концентрацию ионов железа в растворе:

a(Fe²⁺) = f(Fe²⁺)∙C_m(Fe²⁺), следовательно, C_m(Fe²⁺) = a(Fe²⁺)/f(Fe²⁺) и тогда C_m(Fe²⁺) = 0,31/0,752 = 0,41 (моль/кг).

Ответ: При уменьшении концентрации ионов Fe²⁺ в растворе до 0,41 моль/кг потенциал электрода уменьшится на 0,015 В.

Пример 6. Расчеты ЭДС гальванического элемента, составление схем

гальванических элементов

1. Вычислите при 45^оС электродвижущую силу гальванического элемента

Cu | (0,1 М) CuSO₄ || (0,02 М)Tl₂SO₄ | Tl.

Кажущаяся степень диссоциации CuSO₄ равна 40%, а Tl₂SO₄ – 87%.

Решение. В представленном гальваническом элементе протекают следующие электродные процессы:

на аноде Cu⁰ – 2ē = Cu²⁺, окисление;

на катоде 2Tl⁺ + 2ē = 2Tl, восстановление.

Согласно уравнению Нернста для ЭДС такого гальванического элемента (уравнение 14)

Е = Е⁰ + ℓn , где Е⁰ = φ⁰_Tl⁺_/Tl – φ⁰_Cu/Cu²⁺.

Значения стандартных электродных потенциалов медного и таллиевого электродов найдем по Таблице № 1 Приложения: φ⁰_Tl⁺_/Tl = - 0,34 В; φ⁰_Cu/Cu²⁺ = - 0,34 В. Отсюда следует, что Е⁰ = 0.

Для расчета второго слагаемого в уравнении Нернста вводим допущение, что при низких концентрациях молярная и моляльная концентрации ионов в растворе практически равны между собой, т.е. C_μ ≈ C_m, и тогда, с учетом значений степени диссоциации солей меди сульфата и таллия сульфата, находим:

C_m(Cu²⁺) = α∙C_μ(CuSO₄) = 0,4∙0,1 = 0,04 (моль/кг);

C_m(Tl⁺) = 2∙α∙C_μ(Tl₂SO₄) = 2∙0,87∙0,02 = 0,035 (моль/кг).

Теперь рассчитаем ЭДС, используя упрощенную формулу:

Е = ℓg , где N_e = 2, Т = 273 + 45 = 318 К, и тогда

Е = ℓg = 0,0318∙ℓg(0,031)= 0,0318∙(-1,514) = - 0,048 (В).

Ответ: Е = - 0,048 В.

2. Определите, какие процессы происходят у электродов медного концентрационного гальванического элемента, если у одного из электродов а(Cu²⁺) = 1 моль/кг, а у другого – 1,0∙10^-3 моль/кг. Составьте схему работы этого гальванического элемента и определите его ЭДС.

Решение. В концентрационном гальваническом элементе у электрода с большей активностью действующих ионов протекает процесс восстановления ионов (этот электрод – катод), противоположный электрод с меньшей aктивностью ионов играет роль анода, на нем протекает процесс окисления (как правило, окисляется сам электрод, если он изготовлен из того же металла).

Таким образом, на катоде протекает реакция: Cu²⁺ + 2ē = Cu⁰;

на аноде Cu⁰ - 2ē = Cu²⁺.

В результате этих процессов у катода активность ионов меди уменьшается, а у анода – увеличивается, процесс будет продолжаться до тех пор, пока активности ионов у электродов не сравняются, т.е. а(Cu²⁺)_K = a(Cu²⁺)_A.

Схема гальванического элемента:

(A, –) Сu | Cu²⁺(a = 1,0∙10^-3) || Cu²⁺(a = 1,0) | Cu (K, +).

ЭДС такого гальванического элемента в начальный момент времени будет равна

Е = ℓn = ℓg = = 0,089 B.

Ответ: Е = 0,089 В.

3. Установите, как должен быть составлен гальванический элемент, чтобы в нем протекала реакция

2Au³⁺ + 3H₂ = 2Au + 6H⁺.

Составьте схему работы такого гальванического элемента и рассчитайте его стандартную ЭДС.

Решение. Уравнение окислительно-восстановительного процесса указывает на то, что окислителем в нем выступает катион золота Au³⁺, а восстановителем – газообразный водород Н₂. Следовательно, в гальваническом элементе водородный электрод служит анодом φ(Н₂|2Н⁺)_А, а золотой электрод – катодом φ(Au³⁺/Au)_K, электрический ток перемещается от водородного электрода к золотому, и тогда схема гальванического элемента будет следующей:

(A, –) H₂(Pt) | 2H⁺ || Au³⁺ | Au (K, +).

Стандартная ЭДС такого гальванического элемента определяется по уравнению Нернста как разность стандартных электродных потенциалов катода (золотого электрода) и анода (водородного электрода), т.е.

Е⁰ = φ⁰(Au³⁺/Au) – φ⁰(2Н⁺/Н₂),

и поскольку стандартный электродный потенциал водородного электрода принят равным нулю, то Е⁰ = φ⁰(Au³⁺/Au).

Найдем значение этого потенциала в Таблице № 1 Приложения:

φ⁰(Au³⁺/Au) = 1,50 В и тогда Е⁰ = 1,50 В.

Ответ: Е⁰ = 1,50 В.

4. В гальваническом элементе

(-) Zn |Zn²⁺ || HCl (0,001 M, α = 100%) | H₂(Cu) (+)

концентрация ионов Zn²⁺ в растворе С_μ(Zn²⁺) = 2,1∙10^-3 моль/л. Рассчитайте ЭДС этого элемента при температуре 60⁰С и напишите уравнения его электродных процессов.

Решение. Поскольку в данном гальваническом элементе цинковый электрод является анодом, а водородный – катодом, то в нем идут следующие электродные процессы: а) на аноде - процесс окисления Zn - 2ē = Zn²⁺;

б) на катоде – процесс восстановления 2H⁺ + 2ē = H₂.

Согласно уравнению (14) ЭДС гальванического элемента определяется по формуле

Е = Е⁰ + ℓn .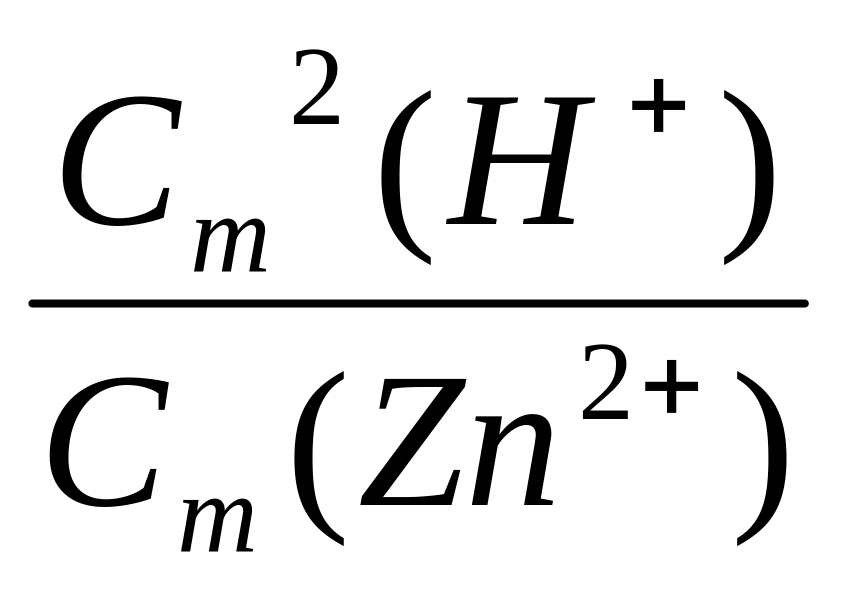

По таблице № 1 Приложения найдем значение стандартного электродного потенциала цинка φ⁰(Zn²⁺/Zn) и рассчитаем стандартную ЭДС, зная что φ⁰(2Н⁺/Н₂) = 0:

Е⁰ = φ⁰(2Н⁺/Н₂) - φ⁰(Zn²⁺/Zn) = 0 – (-0,736) = 0,763 B.

Подставим полученное значение в уравнение Нернста и упростим его с учетом условий задачи, имея в виду, что Т = 273 + 60 = 333 К и N_e = 2:

Е = Е⁰ + ℓg ,

Е = 0,763 + ℓg = 0,763 + 0,033 ℓg(0,48∙10^-3) = 0,653 (В).

Ответ: Е = 0,653 В; на катоде 2H⁺ + 2ē = H₂; на аноде Zn - 2ē = Zn²⁺.