10 Скфу Ляхов в. Ф. Лекции по учебной дисциплине «Информатика»
Лекция 11. Введение в теорию кодирования
Вопросы лекции:
11.1 Основы экономного кодирования
11.2 Кодеры, основанные на системе сжатия без потерь информации
11.3 Основные методы побуквенного кодирования. Код Хаффмана
Литература: Томас Х. Кормен и др. Алгоритмы: построение и анализ = Introduction to Algorithms. – 2-е изд. – М.: Вильямс, 2006.
Введение
На рисунке 11.1 представлена упрощенная структурная схема типичной системы передачи или хранения информации.
Рисунок 11.1 – Упрощенная структурная схема типичной системы передачи или хранения информации
Кодирующие устройство, в общем случае, может выполнять следующие операции:
Согласование источника с каналом (например, перевод реальных сообщений в электрические сигналы, модуляция непрерывных сигналов, квантование непрерывных сигналов, представление дискретного сообщения длины n из символов алфавита A кодом с основанием m).
Экономное представление информации с минимальной избыточностью; или, наоборот, разумное введение избыточности с целью повышения помехоустойчивости сообщения.
Пример операции первого типа: каждой букве русского алфавита ставится в соответствие символ из двоичного алфавита: «A»00000, «Б»00001 и т. д.
Пример операции второго типа: представление графической информации с использованием блочного сжатия (JPEG).
Наибольший практический интерес представляют операции второго типа. Далее рассмотрим теоретические аспекты экономного представления информации, то есть сжатие информации. Здесь выделяют два подхода:
сжатие без потерь информации (неразрушающие сжатие);
сжатие с потерями информации (разрушающие сжатие).
12.1 Основы экономного кодирования
12.1.1 Сжатие без потерь информации
Схема сжатия без потерь показана на рисунке 11.2.
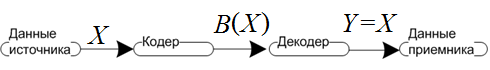
Рисунок 11.2 – Схема сжатия без потерь
На рисунке 12.2 использованы следующие обозначения:
X – это последовательность длины n из символов алфавита A;
B(X) – сжатые данные, представленные во второй последовательности длины m (в общем случае m зависит от n);
Y – декодированные (восстановленные) данные.
В системах неразрушающего сжатия декодер восстанавливает данные источника абсолютно без потерь, т. е. Y = X (рисунок 11.2).
Введем термин «Коэффициент сжатия информации» или просто «Коэффициент сжатия»:
|
(11.1) |
.
12.1.2 Сжатие с потерями информации
На рисунке 11.3 приведена система разрушающего сжатия информации.
Рисунок 11.3 – Схема сжатия с потерями
Квантователь
понижает размер алфавита (например,
округление данных). Между
и
есть однозначное соответствие, но
система в целом остается разрушающей,
так как двум различным последовательностям
и
может соответствовать один и тот же
.
Для сжатия с потерями информации вводят такое понятие, как искажение:
|
(11.2) |
.
Искажение является
мерой среднеквадратичного различия
между сообщениями
и
.
В лекционном курсе будут рассматриваться только кодеры, основанные на системе сжатия без потерь информации.