2. Теоретическая часть 2.1.Частица в невозмущенном прямоугольном потенциале
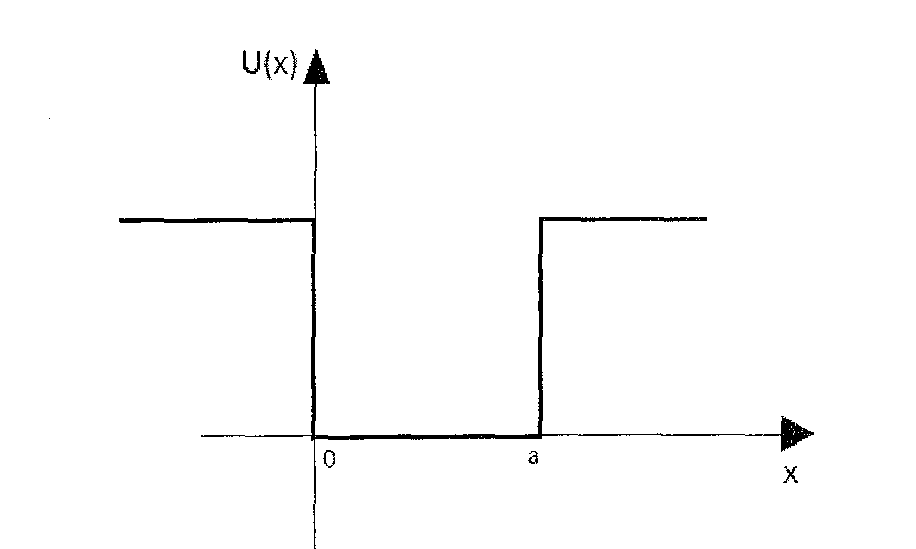
Рис 1. Прямоугольная потенциальная яма.
Рассмотрим микрочастицу, которая может совершать одномерное движение. Потенциальная энергия частицы в этой яме:
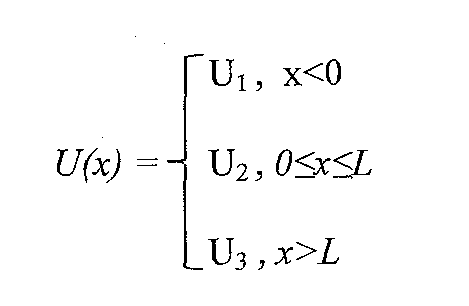
Пусть потенциальная энергия в области 2 равна нулю, а в областях 1 и 3 потенциальная энергия равна высоте ямы:
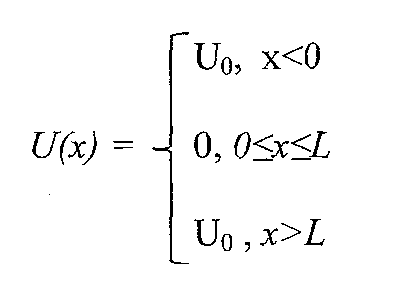
Чтобы описать движение квантовой частицы, решение уравнения Шрёдингера найдём сначала в отдельных областях 1, 2 и 3, затем потребуем непрерывности волновой функции и её производной на границах областей, в точках х = 0 и х = L
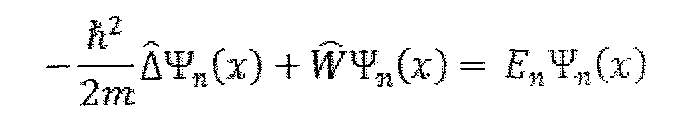
Решение в области 1:
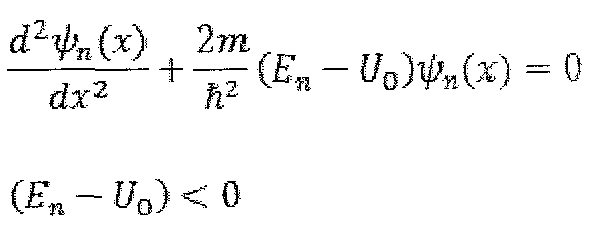
Обозначим:
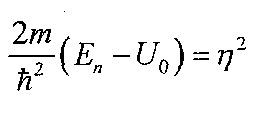
Теперь:
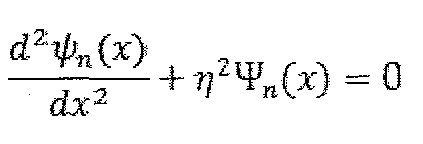
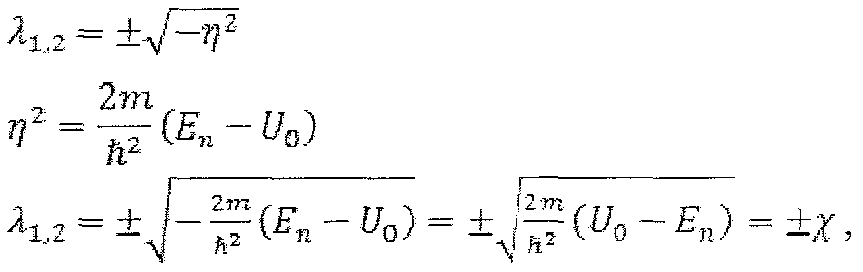
Получили однородное дифференциальное уравнение с
постоянными коэффициентами. Решение этого уравнения имеет вид:
,
где
корни характеристического
уравнения,
которое в данном случае имеет вид:
Корни характеристического уравнения:
-
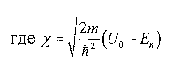действительная
величина
Решение
дифференциального уравнения
здесь А1 и А2 - произвольные постоянные.
Решение в области 2:
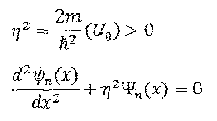
Решение этого уравнения имеет вид:
,
где
корни
характеристического
уравнения,
которое в данном случае имеет вид: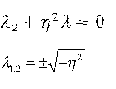
Корни характеристического уравнения мнимые:
-
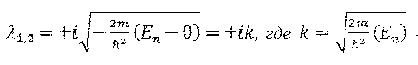действительная
величина Решение дифференциального уравнения:
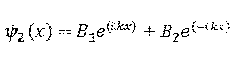
Это решение можно представит в действительной форме:
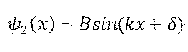
В области 3 решение находим аналогично решению в области 1:
Получили решения-уравнения Шрёдингера областях 1, 2 и 3:
действительная величина
Решение дифференциального уравнения здесь А1 и А2 - произвольные постоянные.
Решение в области 2:
Решение этого уравнения имеет вид:
где
корни характеристического
уравнения, которое в данном случае имеет вид:
Корни характеристического уравнения мнимые:
действительная
величина Решение дифференциального уравнения:
Это решение можно представит в действительной форме:
В области 3 решение находим аналогично решению в области 1:
Получили решения-уравнения Шрёдингера областях 1, 2 и 3:
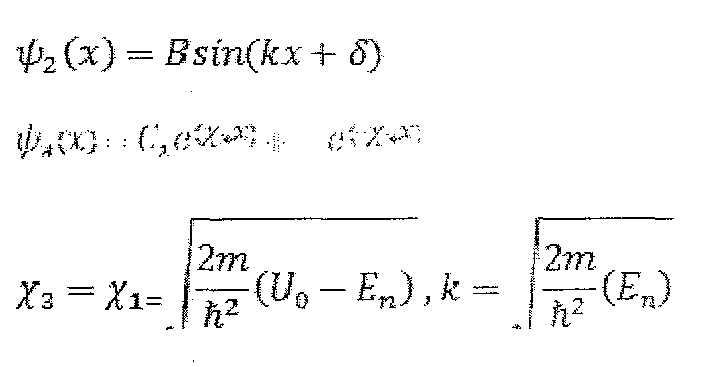
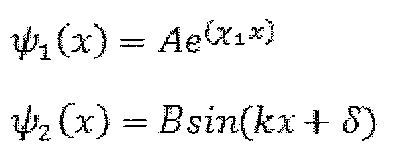
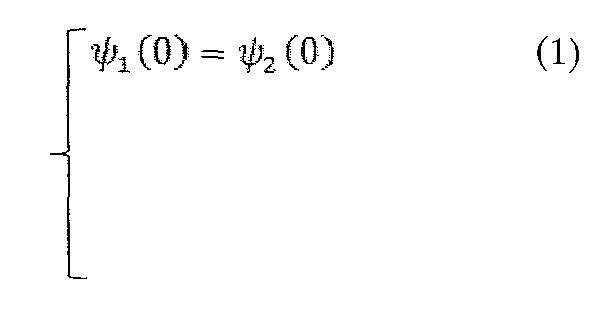
Ч1 N
Волновые функции можно рассматривать, как плоские волны.
Волну вида можно считать волной, распространяющейся вдоль положительного направления оси ОХ.
А волну вида можно считать волной, распространяющейся вдоль отрицательного направления оси ОХ.
Таким образом, решение уравнения Шрёдингера в области 1 можно рассматривать, как суперпозицию волны, падающей на барьер слева и волны, отраженной от барьера и распространяющейся вправо.
Аналогично, решение уравнения Шрёдингера в области 3 можно рассматривать, как суперпозицию волны, падающей на барьер справа и волны, прошедшей через барьер и распространяющейся вправо.
Если считать, что мы рассматриваем частицу, падающую на барьер слева, то в области 3 (за барьером) может существовать только прошедшая волна. Поэтому коэффициент ВЗ при волне, идущей из бесконечности к барьеру можно считать равным нулю.
Решения уравнения Шрёдингера в областях 1, 2 и 3:
Условия непрерывности волновой функции и её первой производной:
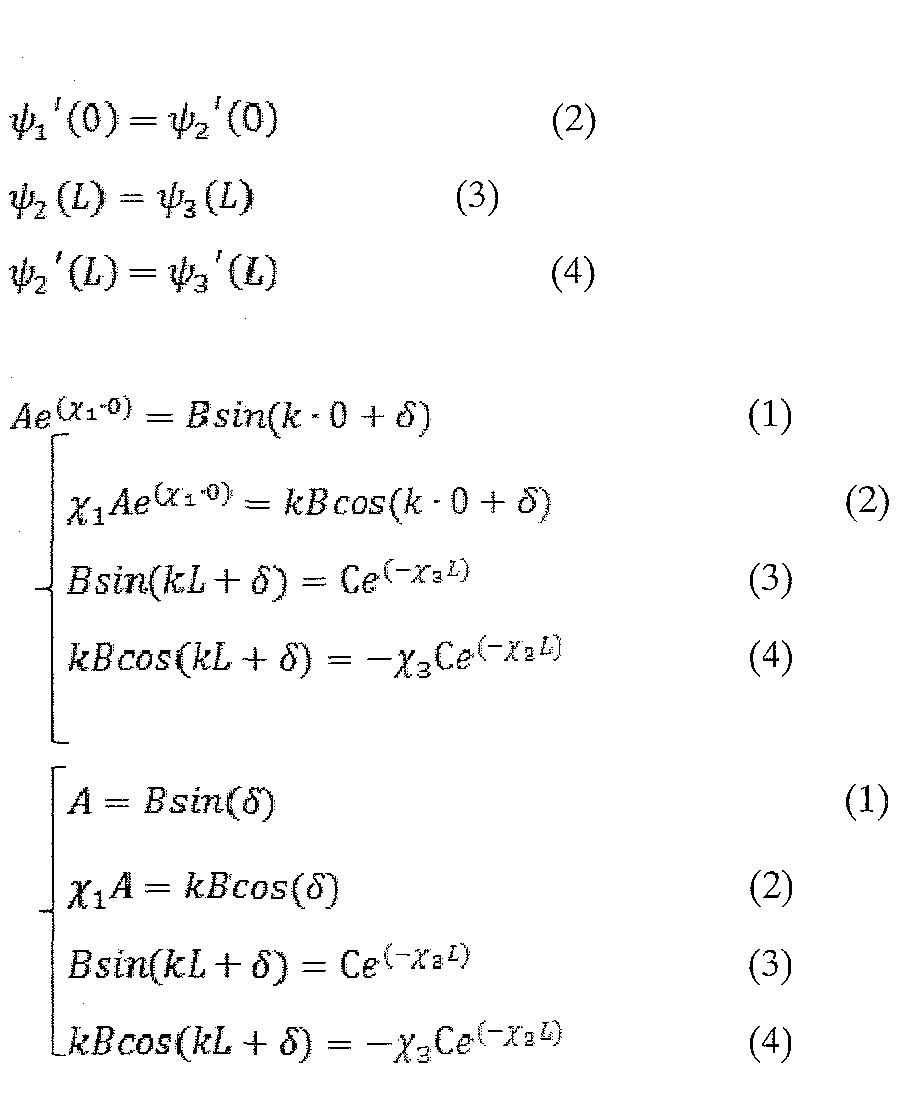
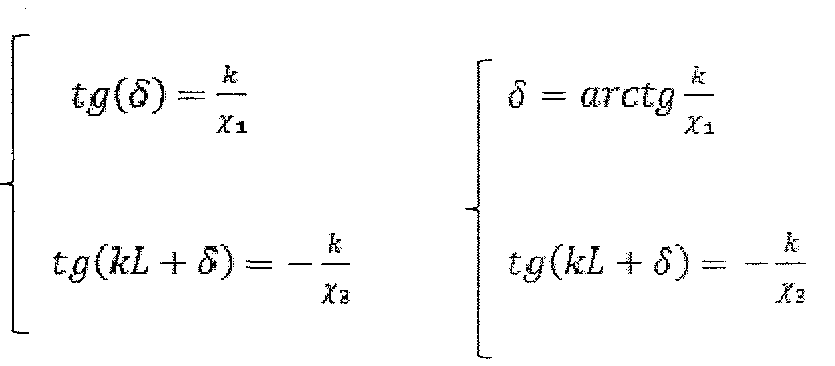
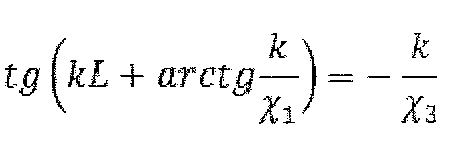
Разделим уравнение (1) на уравнение (2) , а уравнение (3) на уравнение(4):
Получили трансцендентное уравнение:
Решением этого уравнения являются возможные уровни энергии, занимаемые электроном в невозмущенной яме. Для каждого значения энергии находим волновую функцию. Для этого определим коэффициенты А, В, С. Рассмотрим систему уравнений, возникающую из условий непрерывности волновой функции и её производной.
Разделим уравнение (1) на уравнение (2).
Из уравнения (3):
Из уравнения (1):
Для определения константы А воспользуемся условием нормировки волновой функции.
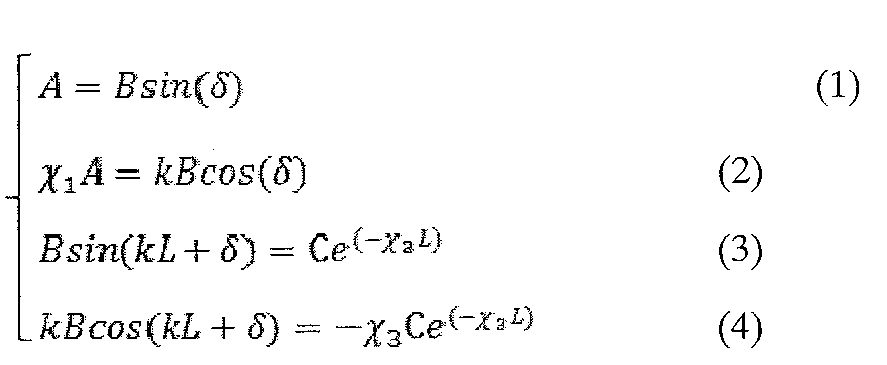
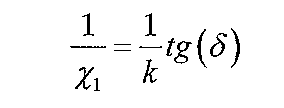
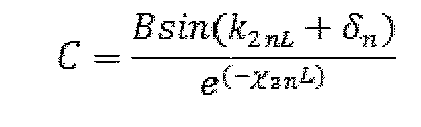
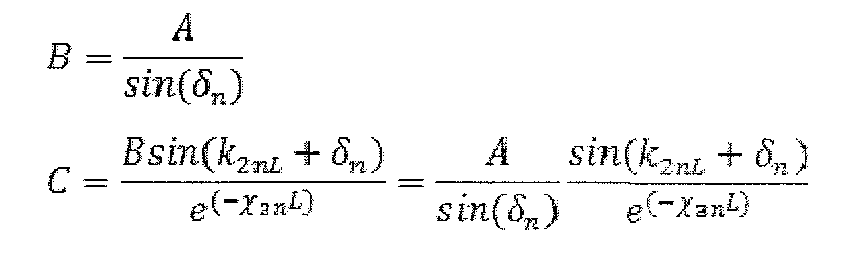
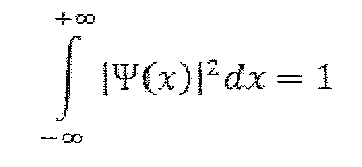
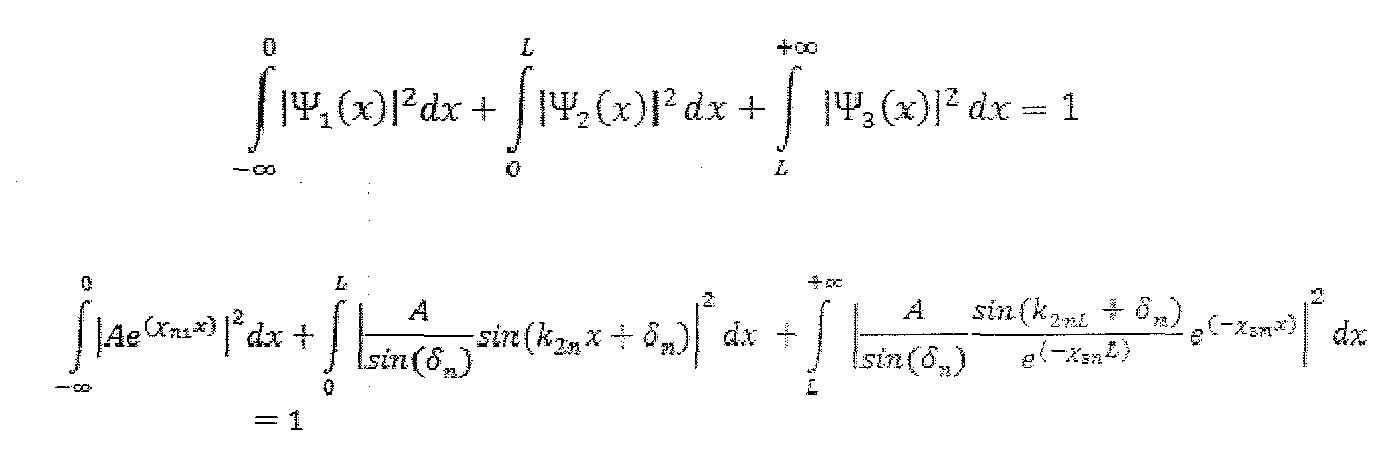
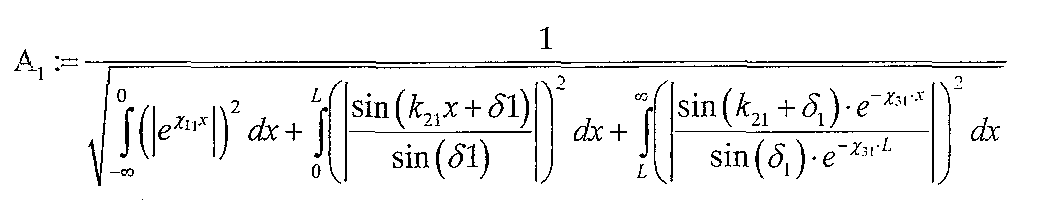
Отсюда: