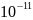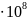2.3 Напряжения изгиба от сил газов

Напряжения изгиба от сил газов определяется по изгибающим моментам относительно главных осей инерции сечения.

П оложения главных осей инерции находится по общим методам сопротивления материалов. Для практический расчётов принимаем, что ость наименьшей жесткости ξ проходит через центр тяжести сечения параллельно хорде профиля (рис. 1.4) Рис.1.4. Профили сечения лопаток.

Положительное направление оси берётся по направлению от входа к выходу потока с лопатки.

Ось η проходит через центр тяжести сечения, перпендикулярно оси ξ, причём положительное направление оси выбирается от вогнутой части профиля к выпуклой.

Для определения изгибающих моментов M_x и M_y относительно осей O­_x и O_y необходимо знать интенсивности нагрузок P_x и P_y , отнесённых к единице длины лопатки и действующих на лопатку в направлении указанных осей. Приближённо считаем, что интенсивность нагрузки постоянна по длине и равна интенсивности нагрузки на среднем радиусе лопатки:

(1.9)

(1.10)

Изгибные моменты относительно осей O­_x и O_y выразятся следующими зависимостями:

(1.11)

(1.12)

Где R – текущий радиус.

Результат расчёта сводим в Таблицу 3.2 и строим графики .

Таблица 1.2.

Номер сечения	R м
1	0.254	0	0	0
2	0.226	0.00037	-0.168	-0.37
3	0.199	0.00151	-0.671	-1.481

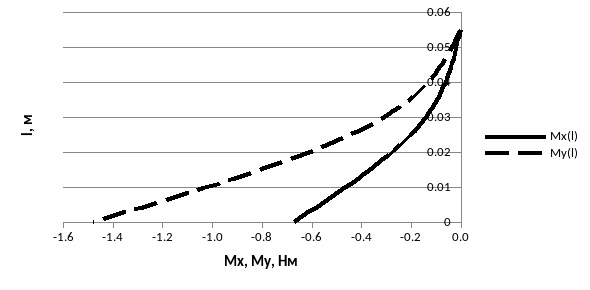
Рис.1.5 Графики .

Для каждого из выбранных сечений лопатки необходимо найти напряжения изгиба в трёх точках ( А, В и С), наиболее удалённых от оси наименьшей жёсткости.

Для этого надо знать моменты инерции относительно осей

Определение моментов инерции можно вести любым из известных способов. Приближённо их можно определить с помощью сеток или по приближённым формулам:

. (1.13)

. (1.14)

Координаты центра тяжести профиля выражаются следующими зависимостями:

. (1.15)

. (1.16)

Значения моментов инерции и координат центра тяжести записываем в Таблицу1.3.

Таблица 1.3.

Номер сечения	b м	h м	м	I м4	I м4	m м	n м
1	0.01359	0.000877	0.00082	0.06426	7.821	5.83	0.66
2	0.01641	0.001211	0.00147	0.35	24.68	7.04	0.92
3	0.02075	0.001951	0.00249	2.068	84.54	8.902	1.48

По чертежу определяем координаты точек А, В и С сечения и записываем их в Таблицу 1.4.

Таблица 1.4.

Номер сечения	a	b	c	a	b	c
1	-5.83·10-3	0	7.76·10-3	-6.683·10-4	6.187·10-4	-6.683·10-4
2	-7.04·10-3	0	9.37·10-3	-9.228·10-4	1.023·10-3	-9.228·10-4
3	-8.902·10-3	0	0.012	-1.487·10-3	1.709·10-3	-1.487·10-3

Определяем проекции изгибающих моментов M_x и M_y на оси и η по формулам:

M_ξ = ± М_хcosβ ± M_ysinβ. (1.17)

Мη = М_хsinβ - M_ycosβ. (1.18)

Где β - угол между осями 0_х и 0_ξ измеряется по чертежу. При вычислении момента М_ξ верхние знаки перед слагаемыми относятся к лопаткам турбины, а нижние – к лопаткам компрессора. Результаты расчёта по формулам сводим в Таблицу 1.5.

Таблица 1.5

Номер сечения	β°	Mξ Hм	Mη Hм
1	62.89	0	0
2	55.96	0.401	0.068
3	51.21	1.575	0.404

Напряжение изгиба в точках А В С в принятых сечениях выразятся формулами

, (1.19)

, (1.20)

, (1.21)

По результатам расчёта строим графики :σ_ua = f(l); σ_ub = f(l); σ_uc = f(l).

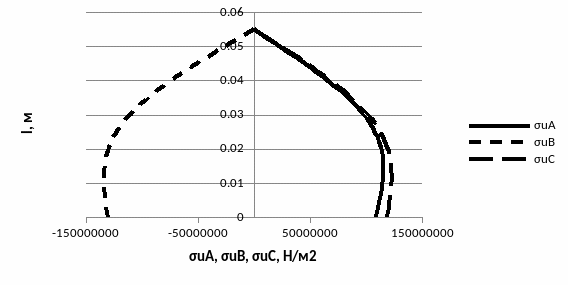
Рис. 1.6 Графики σ_ua = f(l); σ_ub = f(l); σ_uc = f(l).

В каждом сечении для наиболее нагруженной точки профиля определяем суммарное напряжение от изгиба газовыми и растяжными центробежными силами:

σ_Σmax = σ_u + σ_p. (1.21)

Результаты расчёта по формулам сводим в Таблицу 1.6 и строим графики зависимости σ_Σmax=f(l), σ_р=f(l), σ_иа=f(l).

Таблица 1.6

Номер сечения	σuA H/м2	σuB H/м2	σuC H/м2	σр H/м2	σΣmax H/м2
1	0		0	0	0
2	1.037	-1.172	1.082	5.391	6.563
3	1.09	-1.302	1.189	7.309	8.611

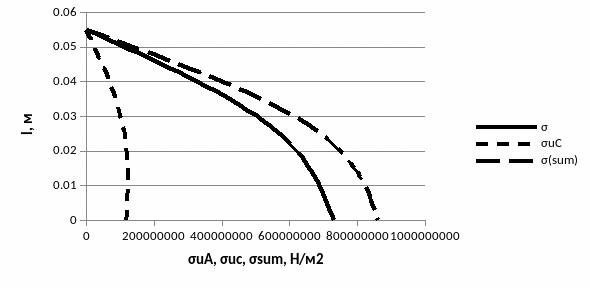
Рис. 1.7. Графики зависимости σ_Σmax=f(l), σ_р=f(l), σ_иа=f(l).

В результате расчётов было выявлено, что суммарное напряжение в точке «B» - максимально.