7.1. Уравнения вида

Рассмотрим сначала уравнение n-го порядка вида

, (7.1)

где – непрерывная функция, .

Общее решение уравнения (7.1) может быть получено путем n последовательных интегрирований

,

,

причем оно будет зависеть от n констант .

Пример 7.1. Найти общее решение уравнения .

Решение: В данном случае (см. (7.1)) n = 3, . Определим последовательно функции . Получим

Ответ:

Пример 7.2. Решить задачу Коши , .

Решение: Имеем (см. (7.1)) n = 2, . Последовательно находим функции , на каждом шаге определяя константы из условий .

На первом шаге (интегрируя по частям)

и, учитывая, что , находим константу С₁:

На втором шаге (интегрируя по частям)

учитывая, что , находим константу С₂:

Итак, – частное решение, удовлетворяющее условию .

7.2. Уравнения вида

Рассмотрим дифференциальное уравнение n-го порядка вида

, (7.2)

не содержащее искомой функции и ее производных до ( )-го порядка включительно (то есть функции ).

Уравнение (7.2) введением новой функции

(7.3)

( ) сводится к дифференциальному уравнению первого порядка

, (7.4)

где неизвестной является функция (x – независимая переменная).

Найдя решение уравнения (7.4) – функцию , получаем дифференциальное уравнение вида

(7.5)

относительно неизвестной функции , и являющееся уравнением вида (7.1). Решение уравнения (7.5) может быть получено путем (n–1) последовательных интегрирований.

В частном случае, когда n=2 дифференциальное уравнение (7.2) является уравнением второго порядка . Тогда замена (7.3), которая здесь имеет вид , также приводит уравнение (7.2) к дифференциальному уравнению первого порядка (7.4).

Пример 7.3. Найти общее решение уравнения

. (7.6)

Решение: Представленное уравнение (7.6) является дифференциальным уравнением третьего порядка (n=3), которое можно записать в виде (7.2)

.

Заменой уравнение (7.6) приводится к уравнению

(7.7)

с разделяющимися переменными относительно функции . Решаем его:

При получили . Однако является частным решением уравнения (7.7). Тогда общее решение уравнения (7.7) можно записать в виде (частное решение входит сюда при ).

Учитывая, что , находим последовательно функции

Ответ:

Пример 7.4. Найти общее решение уравнения

. (7.8)

Решение: Уравнение (7.8) является дифференциальным уравнением второго порядка (n=2), . Примем , тогда и уравнение (7.8) примет вид

.

Разрешив это уравнение относительно своей производной, получим

. (7.9)

Уравнение (7.9), очевидно, является однородным дифференциальным уравнением (функция – однородная нулевого порядка (проверьте!)). Решение уравнения (7.9) ищем в виде

, .

Учитывая, что , получим

.

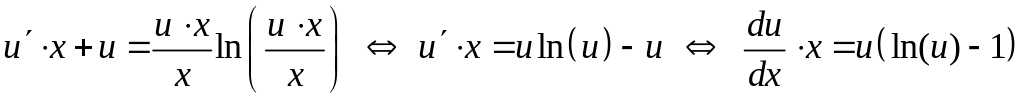Последнее уравнение – уравнение с разделяющимися переменными:

Таким образом, общее решение уравнения (7.9) имеет вид

. (7.10)

Непосредственно проверяется, что при функция не является частным решением уравнения (7.9), а при функция является частным решением уравнения (7.9). Тогда общее решение уравнения (7.9) можно записать в виде

. (7.11)

Теперь, исходя из равенства , нетрудно найти общее решение исходного уравнения (7.8)

Ответ: