11. Горизонтальные асимптоты графика функции

Определение 1. Прямая ( ) называется правой горизонтальной асимптотой к графику функции , если расстояние от этой прямой до графика функции стремится к нулю при .

Определение 2. Прямая ( ) называется левой горизонтальной асимптотой к графику функции , если расстояние от этой прямой до графика функции стремится к нулю при .

Согласно определению, расстояние от горизонтальной асимптоты до графика функции должно стремиться к нулю при удалении точек графика этой функции от начала координат.

Можно показать, что прямая ( ) является правой горизонтальной асимптотой к графику функции , если выполняется условие

, (11.1)

а прямая ( ) является левой горизонтальной асимптотой к графику функции , если выполняется условие

. (11.2)

Если для графика функции правая и левая горизонтальная асимптоты совпадают, то говорят, что график функции имеет горизонтальную асимптоту.

Рассмотрим горизонтальные асимптоты для графиков некоторых простейших элементарных функций.

Степенная функции вида имеет горизонтальную асимптоту (ось абсцисс), так как

К примеру, на рис. 11.1 изображены графики функций (красный цвет), (синий цвет).

Рис. 11.1

График функции (см. рис. 11.2) имеет правую горизонтальную асимптоту (красная прямая) и левую горизонтальную асимптоту (синяя прямая), так как

.

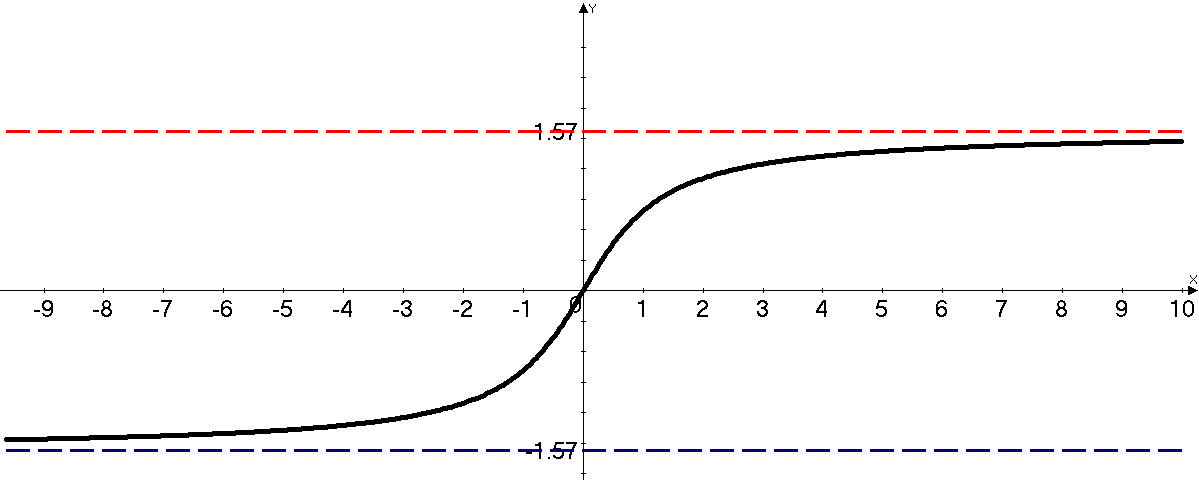
Рис. 11.2

Дробно-рациональная функция

,

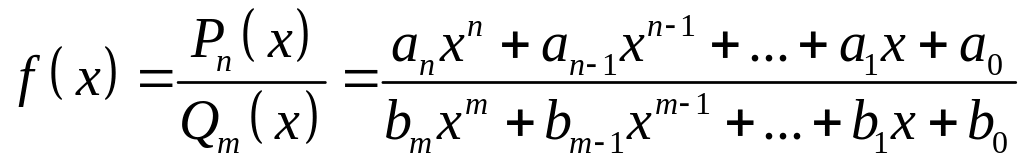где имеет горизонтальную асимптоту, если , причем в случае горизонтальной асимптотой является прямая 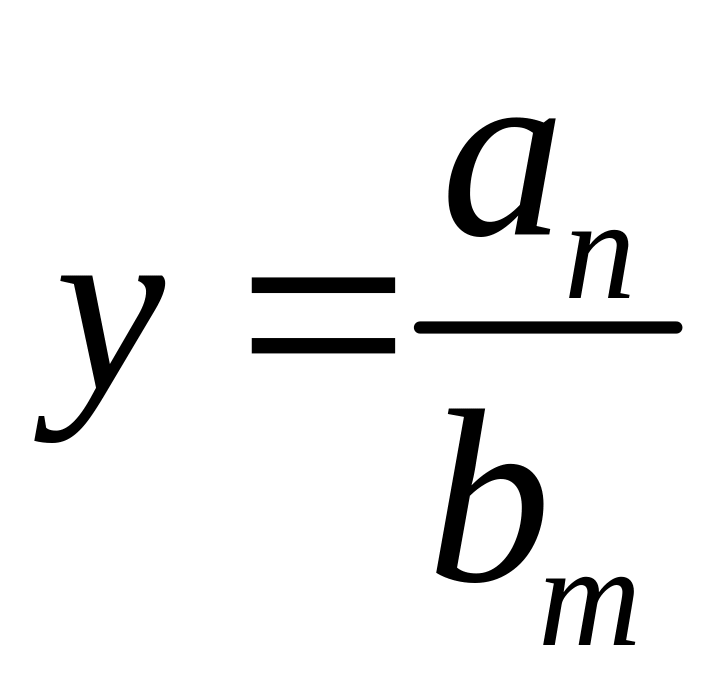, а в случае горизонтальной асимптотой является прямая (ось абсцисс).

Пример 1. Написать уравнение горизонтальной асимптоты к графику функции: 1) 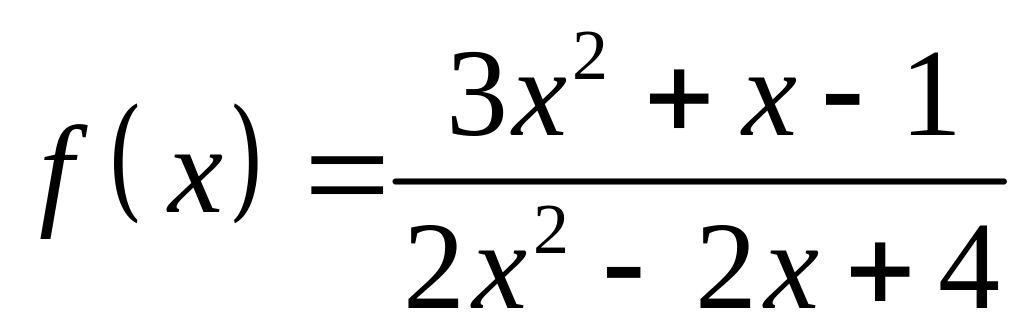, 2) .

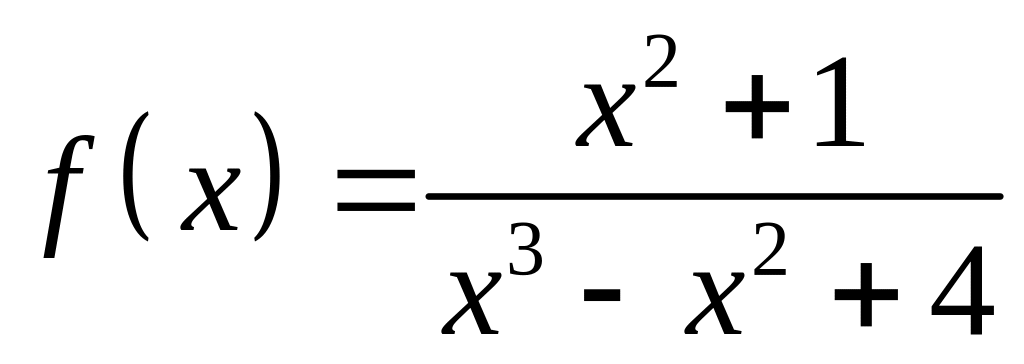Решение. 1) Для графика первой функции горизонтальной асимптотой будет являться прямая , так как

, .

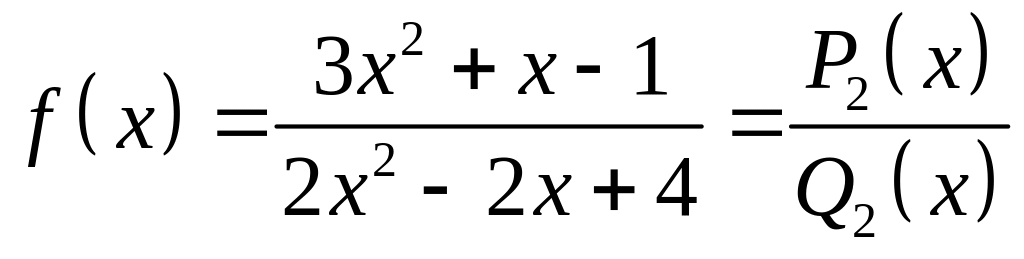2) Для графика второй функции горизонтальной асимптотой будет являться прямая (ось абсцисс), так как

, .

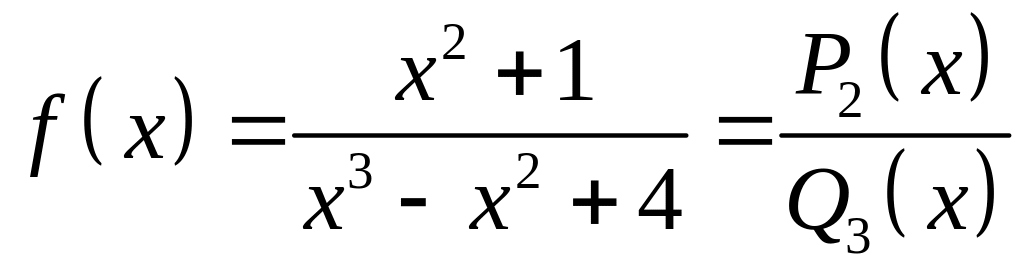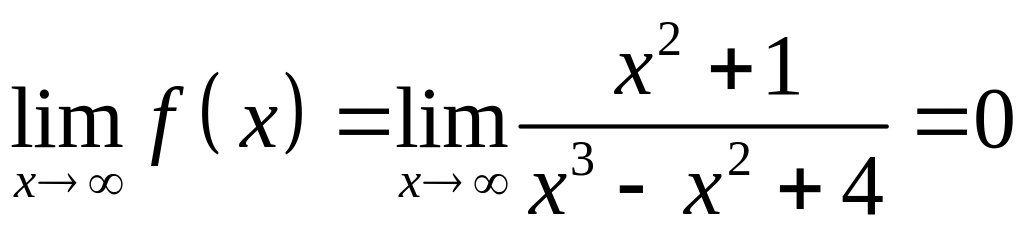Пример 2. Выяснить, имеет ли график функции правую (левую) горизонтальную асимптоту.

Решение. Выясним, имеет ли график функции правую горизонтальную асимптоту. Вычисляем предел функции на :

.

Так как не является конечным пределом, то график функции не имеет правую горизонтальную асимптоту.

Вычисляем предел функции на :

.

Полученную ситуацию неопределенности снимаем с помощью правила Лопиталя, предварительно создав дробь:

.

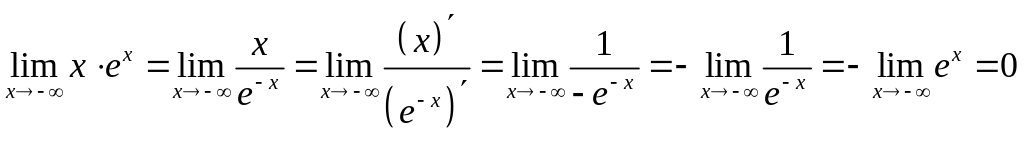Полученный предел показывает, что прямая является левой горизонтальной асимптотой к графику функции.

График функции представлен на рис. 11.3 (левая горизонтальная асимптота к графику функции проведена красным цветом).

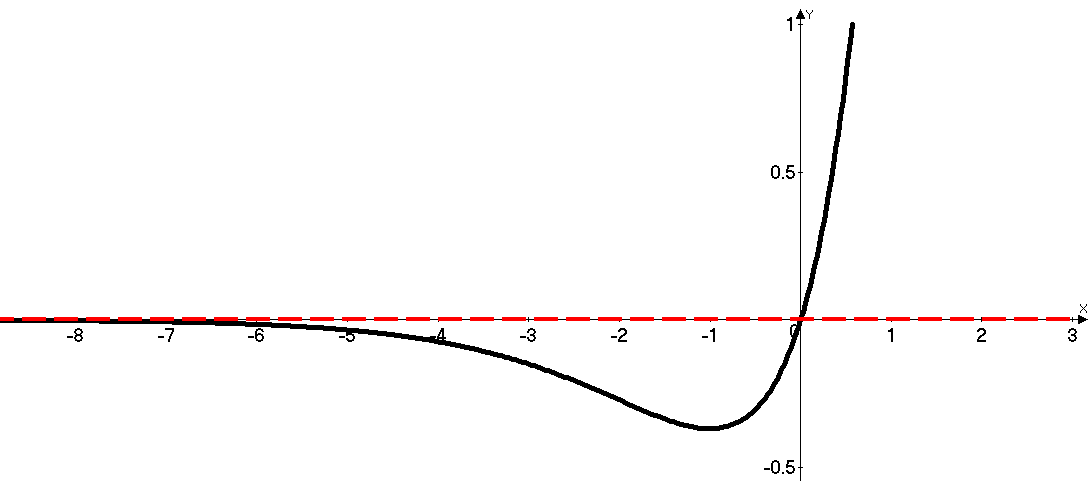
Рис. 11.3

Лекция 7

12. Приложения дифференциального исчисления функции одной переменной к исследованию функции и построению ее графика

Приведем общий план исследования функции:

1). Область определения функции, область значений функции.

2). Непрерывность, точки разрыва (их классификация).

3). Четность, нечетность функции.

4). Асимптоты графика функции (вертикальные, наклонные, горизонтальные).

5). Интервалы монотонности функции, точки экстремума.

6). Интервалы выпуклости функции, точки перегиба.

7). Контрольные точки (пересечение с осями координат, значения функции в точках экстремумов, точках перегиба, другие удобные точки).

8). Построение графика.

Пример 1. Исследовать функцию, построить ее график:

.

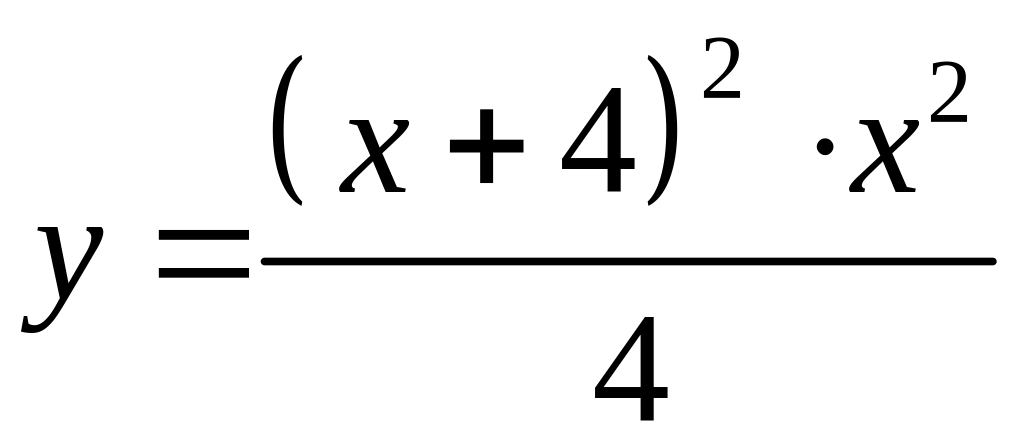Решение. 1). Область определения (функция – многочлен, определенный при всех значениях независимой переменной ), область значений (график полностью расположен выше оси ординат).

2). Функция непрерывна на всей области определения как произведение степенных функций, непрерывных при всех . Точек разрыва у функции нет.

3). Функция общего вида, так как и .

4). График функции не имеет вертикальных асимптот, так как функция непрерывна. График функции не имеет наклонных и горизонтальных асимптот, так как коэффициент

.

5). Исследуем функцию на монотонность. Находим первую производную

.

Точками, подозрительными на экстремум, являются

, , .

Убеждаемся, что:

, при ,

, при ,

, при ,

, при .

Имеем следующие три точки экстремума:

(точка минимума),

(точка максимума),

(точка минимума).

6). Исследуем функцию на выпуклость. Находим вторую производную

.

Точки, подозрительные на перегиб, находятся из условия

.

Находим эти точки (округляем до сотых):

,

.

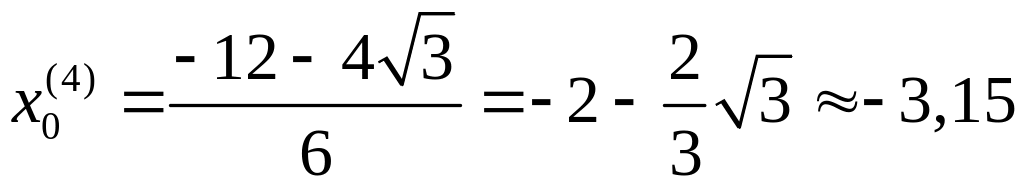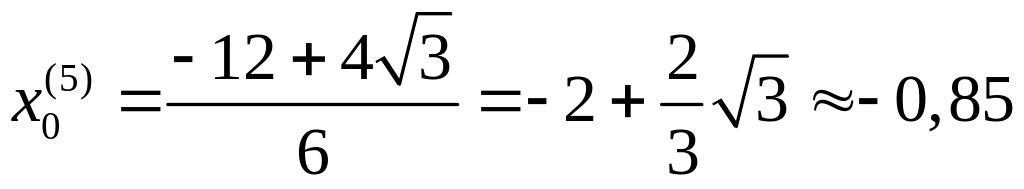Нетрудно установить, что при : (функция выпукла вниз), при : (функция выпукла вверх), при : (функция выпукла вниз). Значит, точки , являются точками перегиба графика функции.

7). Находим точки пересечения графика функции с осями координат: 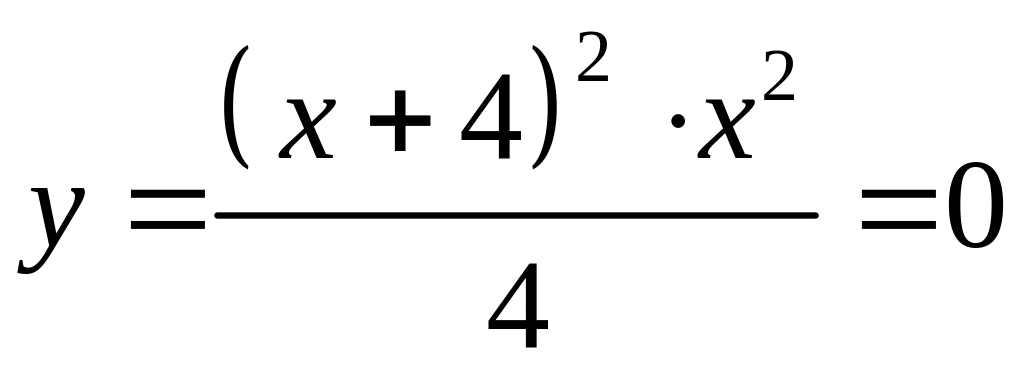при , .

Учитывая точки экстремума и точки перегиба, получаем следующие контрольные точки графика функции: (минимум), (максимум), (минимум), , (перегибы графика).

8). По полученным данным строим график функции (см. рис. 1).

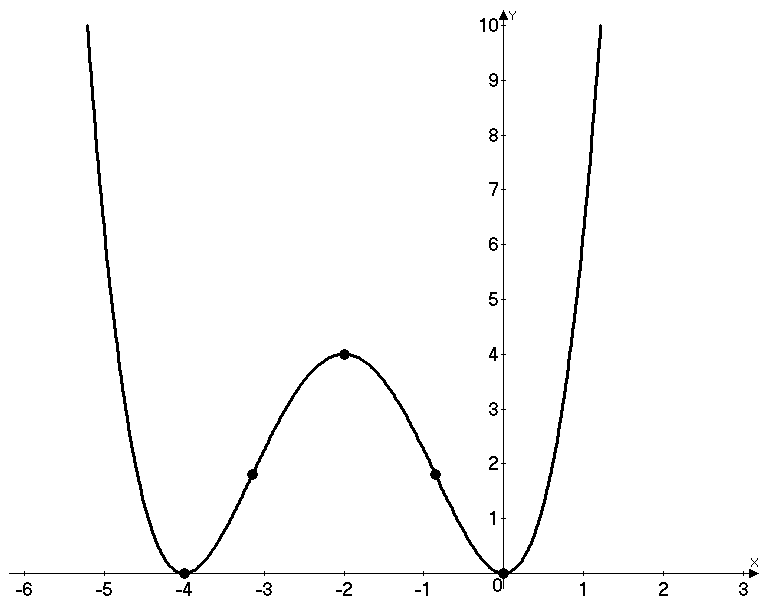
Рис. 1

Пример 2. Исследовать функцию, построить график:

.

Решение.

1). Область определения , область значений , так как функция дробно-рациональная.

2). Функция непрерывна на области определения как дробно-рациональная функция. Так как функция не определена в точке , то исследуем поведение функции в этой точке (вычисляем односторонние пределы):

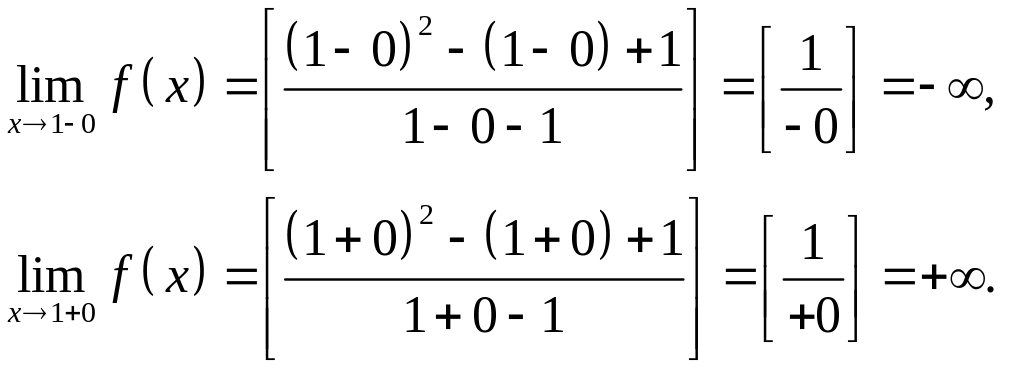
Найденные пределы показывают, что – точка разрыва второго рода.

3). Функция общего вида, так как и .

4). Прямая – вертикальная асимптота (так как – точка разрыва второго рода).

Находим наклонную асимптоту к графику функции

, ,

, .

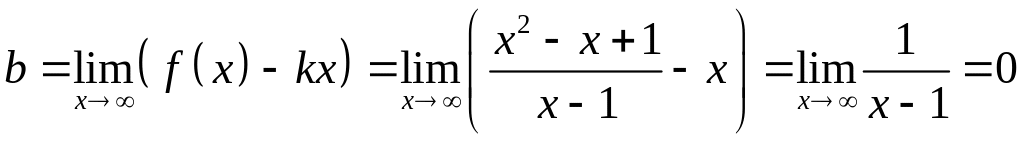Прямая , то есть – наклонная асимптота к графику функции.

5). Исследуем функцию на монотонность. Согласно необходимому условию точки экстремума, находим производную функции

.

Приравнивая найденную производную к нулю, получаем

Точки , – стационарные точки (в них производная обращается в нуль). Они же являются точками возможного экстремума. Точка не является точкой, подозрительной на экстремум, так как в ней функция не определена.

Исследуем знаки производной по методу интервалов. Всю числовую ось разбиваем на четыре интервала точками 0, 1, 2. На каждом из получающихся интервалов берем по одной точке и подставляем в производную:

, ,

, .

Знак производной в конкретной точке показывает знак производной на всем интервале, из которого взята данная точка. Например, так как , то при производная положительна, а значит, функция строго возрастает.

Из метода интервалов следует, что функция строго возрастает при , строго убывает при .

Согласно первому достаточному признаку точки экстремума – точка максимума ( , ), – точка минимума ( , ).

6). Исследуем функцию на выпуклость. Находим вторую производную

.

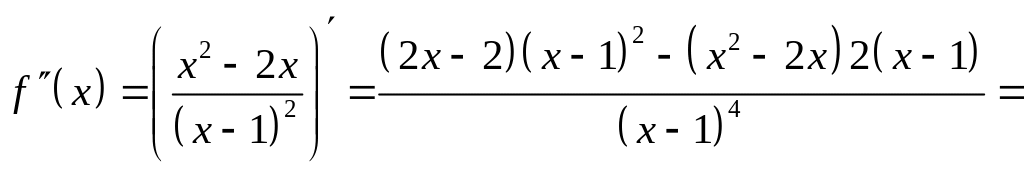
Итак,

.

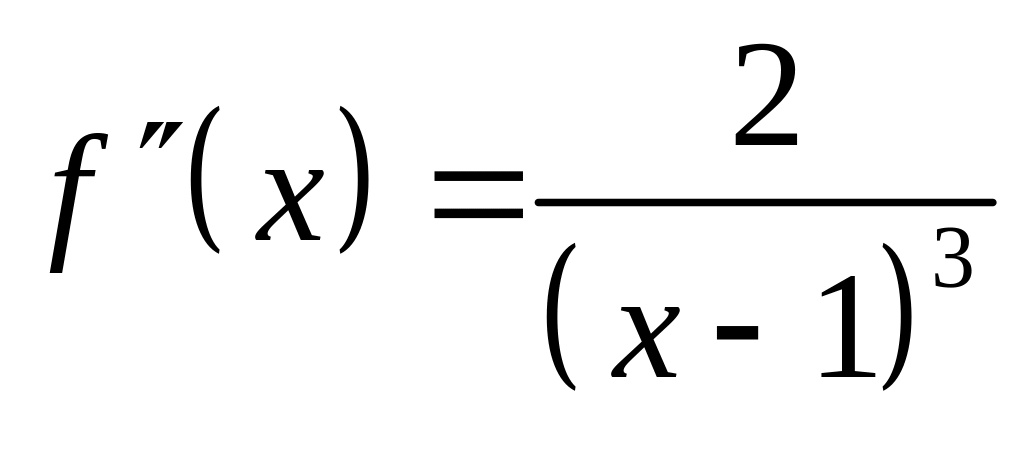Так как вторая производная в нуль не обращается, то функция не имеет точек перегиба.

При : (функция выпукла вверх), при : (функция выпукла вниз).

7). При имеем (контрольная точка – точка максимума). При уравнение не имеет действительных корней (график функции не пересекает ось абсцисс). Далее имеем контрольные точки (точка минимума), , .

8). Для построения графика составим сводную таблицу.

Значения		0		1		2
Характер монотонности	↑	max	↓	не сущ.	↓	min	↑
Характер выпуклости				не сущ.
Значения функции		–1		,		3

График функции изображен на рисунке 2.

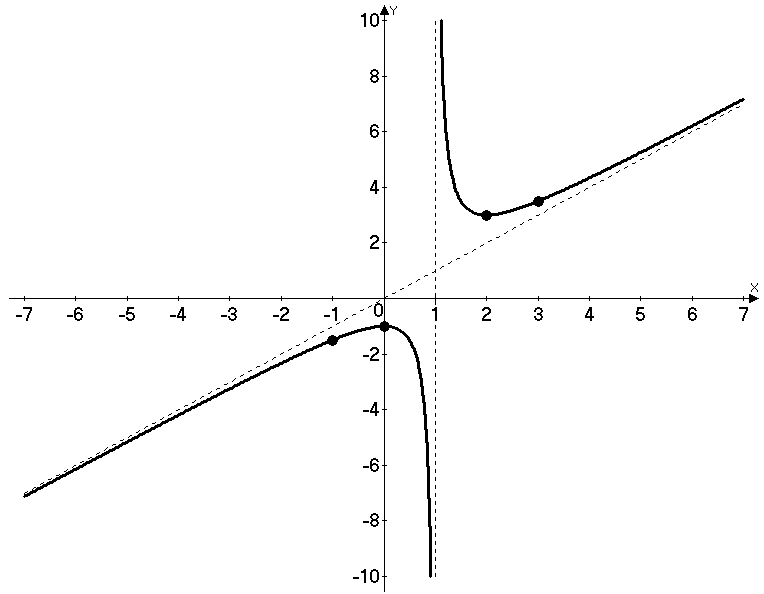
Рис. 2

Пример 3. Исследовать функцию и построить ее график.

Решение.

1). Область определения , область значений .

2). Функция непрерывна на как композиция функций: , , , , непрерывных при . Исследуем поведение функции в точке возможного разрыва (вычисляем односторонние пределы):

,

.

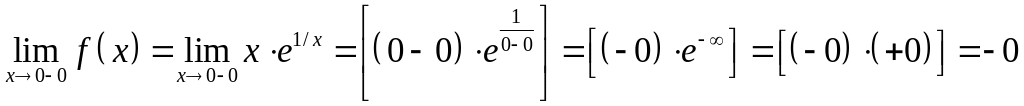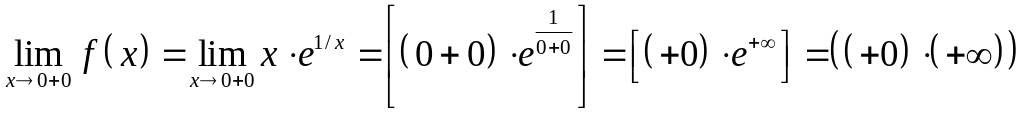Имеем неопределенность вида . Воспользуемся правилом Лопиталя

.

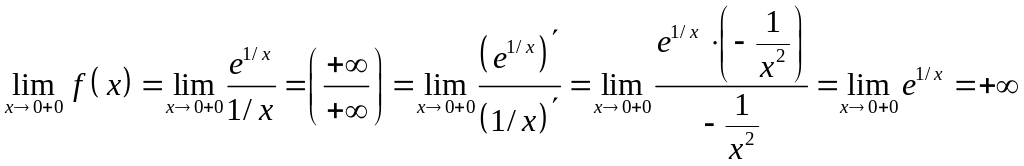Найденные пределы показывают, что – точка разрыва второго рода.

3). Функция общего вида, так как и .

4). Прямая – вертикальная асимптота (так как – точка разрыва второго рода).

Находим наклонную асимптоту:

, ,

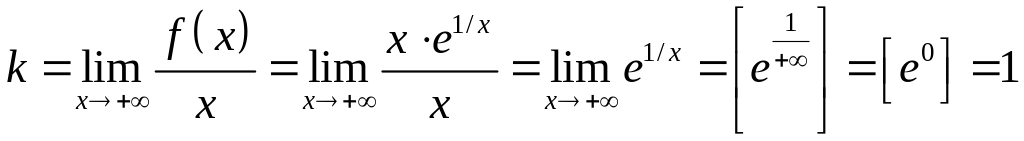(воспользовались эквивалентностью , так как ).

Итак, прямая – наклонная асимптота на (аналогично можно показать, что прямая – наклонная асимптота на ).

5). Первая производная функции равна

.

Знак производной зависит от знака выражения . Методом интервалов непосредственно убеждаемся, что функция монотонно возрастает при

,

монотонно убывает при .

Точка – точка минимума ( , на графике точка ).

6). Вычисляем вторую производную от функции :

.

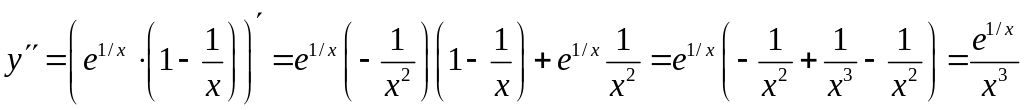Очевидно, что при (функция выпукла вверх), при (функция выпукла вниз), функция не имеет точек перегиба.

7). Контрольные точки: нет пересечений ни с одной из осей координат, на графике функции отмечаем точку минимума .

8). Для построения графика составим сводную таблицу.

Значения		0		1
Характер монотонности	↑	–	↓	min	↑
Характер выпуклости		–
Значения функции		Разрыв 2-го рода, ,

График функции изображен на рис. 3.

Рис. 3