Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рязанский государственный радиотехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Tema_4_Prilozhenia_diff_ischisl_F1P.doc

Скачиваний:

Добавлен:

01.03.2025

Размер:

2.3 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерно-экономический факультет

Кафедра эконометрики и математического моделирования (ЭиММ)

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«Математический анализ»

для направления 080100 «Экономика»

Рязань 2012

Тема 4. Приложения дифференциального

исчисления функции одной переменной

Лекция 1

1. Основные теоремы дифференциального исчисления

Теорема 1 (Ферма). Если функция определена в окрестности точки , принимает в этой точке наибольшее (наименьшее) значение и в точке существует конечная производная , то обязательно .

Доказательство. Пусть для определенности – наибольшее значение функции в окрестности точки (напомним, что под окрестностью точки понимается некоторый достаточно малый интервал, серединой которого является сама точка ). Тогда при всех из этой окрестности:

следовательно, при

, (1.1)

а при

. (1.2)

Из (1.1), (1.2) следует, что . Теорема доказана.

Геометрически теорема Ферма означает, что если в точке функция принимает наибольшее или наименьшее значение и в этой точке существует конечная производная , то касательная, проведенная к графику функции через точку с абсциссой , параллельна оси абсцисс (см. рис).

Действительно, ведь в этом случае, согласно геометрическому смыслу производной функции в точке ( есть угол наклона касательной к оси абсцисс).

Теорема 2 (Ролля). Если функция определена и непрерывна в отрезке , дифференцируема на интервале и принимает равные значения на концах промежутка, то существует точка , что .

Доказательство. По свойству непрерывных функций принимает на наибольшее и наименьшее значения.

Если , то (функция постоянна на отрезке ), следовательно, ( точка - любая точка из интервала ).

Пусть . Так как , то, по крайней мере, одно из значений (М или m) достигается в некоторой точке интервала (см. рис). Тогда на основании теоремы Ферма, .

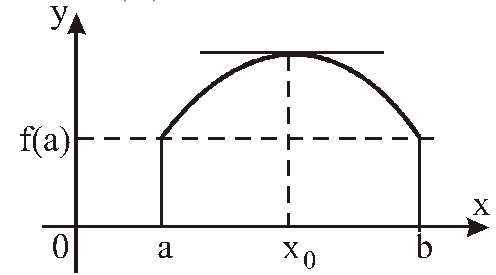
Замечание. Если хотя бы одно из условий теоремы не выполняется, то теорема несправедлива. Например, функция ( ) удовлетворяет всем условиям теоремы Ролля, кроме дифференцируемости в точке , и теорема Ролля несправедлива.

Теорема 3 (Лагранжа). Пусть функция определена и непрерывна на отрезке и имеет конечную производную на интервале . Тогда существует точка такая, что выполняется равенство

Доказательство. Введем в рассмотрение вспомогательную функцию

. (1.3)

Эта функция непрерывна на отрезке , дифференцируема на интервале , причем , так как

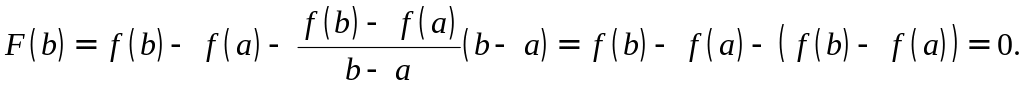
Значит, функция (1.3) удовлетворяет всем условиям теоремы Ролля. Следовательно, существует точка такая, что

откуда . Теорема доказана.

Геометрический смысл теоремы очевиден из рисунка. Касательная к кривой в точке имеет угловой коэффициент

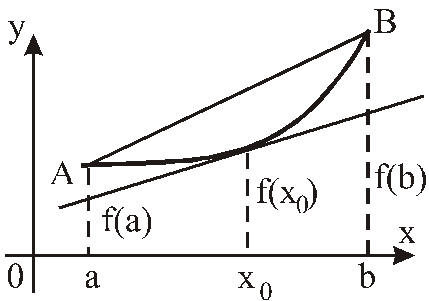
Лекция 2

2. Правило Лопиталя для раскрытия неопределенностей и

Напомним, что при рассмотрении бесконечно больших и бесконечно малых функций мы встретились с неопределенностями:

Используя свойства бесконечно больших и бесконечно малых функций, мы можем раскрывать эти неопределенности.

В дополнении к известным методам нахождения пределов и раскрытия неопределенностей (разложение на множители, метод сопряженных выражений, метод замены, замечательные пределы) приведем здесь простое и удобное правило Лопиталя.

Теорема (правило Лопиталя). Пусть дифференцируемые в окрестности точки функции , при совместно стремятся к нулю или бесконечности. Если отношение их производных имеет предел (конечный или бесконечный) при , то отношение самих функций , также имеет предел при , равный .

Данную теорему можно сформулировать в виде следующей схемы:

Если и , то .

Доказательство. Докажем теорему в некоторых частных случаях.

1) Пусть , , причем , . Докажем, что . Предположим, что . Так как функции , дифференцируемы в точке , то они непрерывны в точке : , . Тогда

2) Пусть , ( ), . Сделаем замену переменной . Тогда при получим . Воспользовавшись результатами пункта 1) ( ), получим

Пример 1. Вычислить пределы:

, , .

Решение.

1) В пределе имеем ситуацию неопределенности .

Для функций , имеем , , причем эти функции дифференцируемы в окрестности нуля:

, .

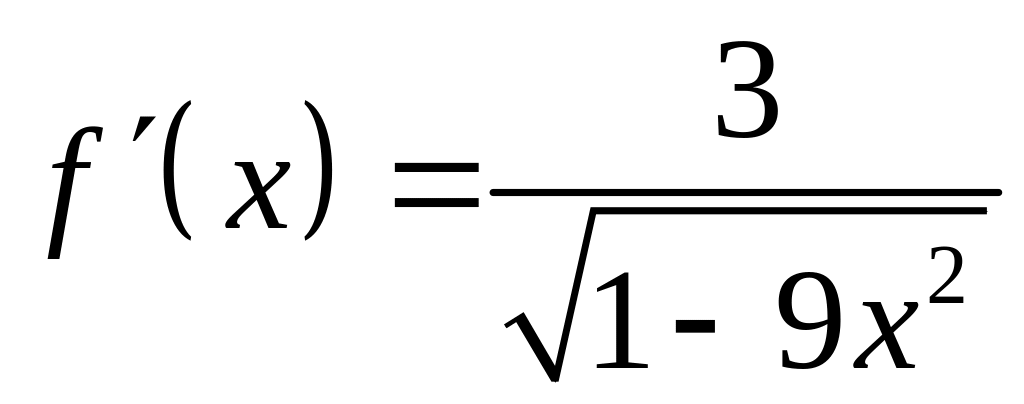Применяя правило Лопиталя, получим

значит, .

2) Имеем , , , , . Применяя правило Лопиталя, получим , значит, .

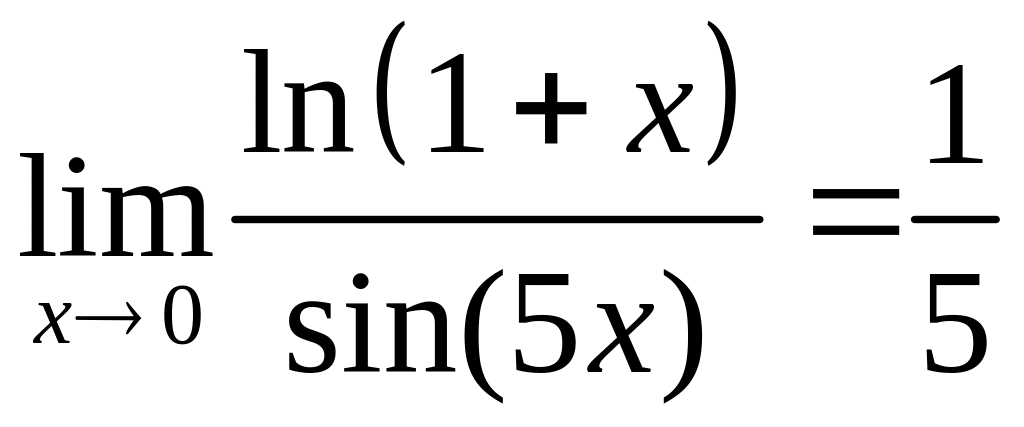3) Вычисляем предел , применяя правило Лопиталя:

Пример 2. Вычислить пределы:

, .

Решение.

1) Вычисляем предел, применяя правило Лопиталя до тех пор, пока не исчезнет неопределенность вида :

2) Вычисляем предел по правилу Лопиталя до исчезновения неопределенности:

Рассмотрим применение правила Лопиталя для раскрытия дополнительных видов неопределенностей

, , , , .

Неопределенность встречается в пределах вида

когда , . Для раскрытия этой неопределенности достаточно применить следующую схему (создать искусственно дробь в пределе)

В результате получим неопределенность , которая раскрывается по правилу Лопиталя.

Пример 3. Вычислить предел .

Решение. Здесь имеем неопределенность вида . Сведем ее к неопределенности :

Неопределенность встречается в пределах вида

когда . Для раскрытия этой неопределенности достаточно применить следующую схему (создать искусственно дробь в пределе)

В результате получим неопределенность , которая раскрывается по правилу Лопиталя.

Пример 4. Вычислить предел .

Решение. В данном случае , , , . При оценке предела имеем неопределенность . Создадим дробь в пределе, для чего приведем функции , к общему знаменателю: