6. Определение представительного критерия

a – то значение весомости, которое должен иметь представительный критерий

b – min уровень коэффициента весомости критерия.

b≥0.07

a>0.9

Σα = 0.92, то

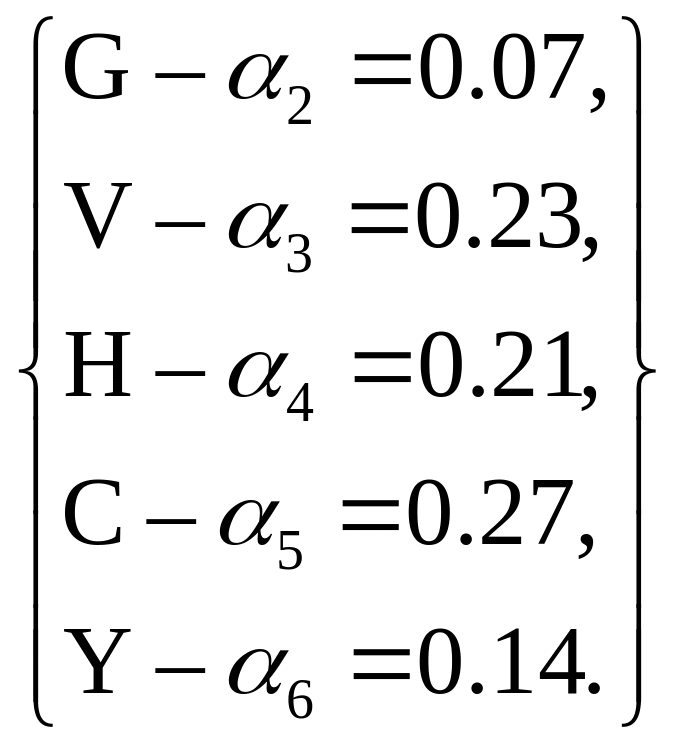
K = (G, V, H, C, Y)

7. Построение матрицы значений критериев вариантов

	G (объем), 10*6	V, МБ	H, ГБ	C, р.	Y
N1	23,76	4096	500	15940	2
N2	27,03	2048	320	17522	5
N3	8,63	4096	500	22769	3
N4	11,44	2048	500	17320	1
N5	9,92	4096	250	10608	4
N ид.	8,63	4096	500	10608	5

8. Формирование модели идеального варианта

Идеальный вариант – тот, который имеет наилучшие значения на множестве известных вариантов.

Определим вид улучшения N:

G – minimiz

V – maximiz

H – maximiz

C – minimiz

Y – maximiz

N ид = (8,63; 4096; 500; 10608; 5).

9. Выбор эффективных вариантов области Парето

Области Парето принадлежат те варианты, которые не доминируются по всей совокупности критериев другими вариантами.

Все варианты принадлежат области Парето, поэтому все варианты – эффективны.

	G (объем), 10*6	V, МБ	H, ГБ	C, р.	Y
N1	23,76	4096	500	15940	2
N2	27,03	2048	320	17522	5
N3	8,63	4096	500	22769	3
N4	11,44	2048	500	17320	1
N5	9,92	4096	250	10608	4
N ид.	8,63	4096	500	10608	5

10. Построение матрицы нормированных значений вариантов

Значения таблицы получаются приведением каждого значения критерия к наилучшему значению.

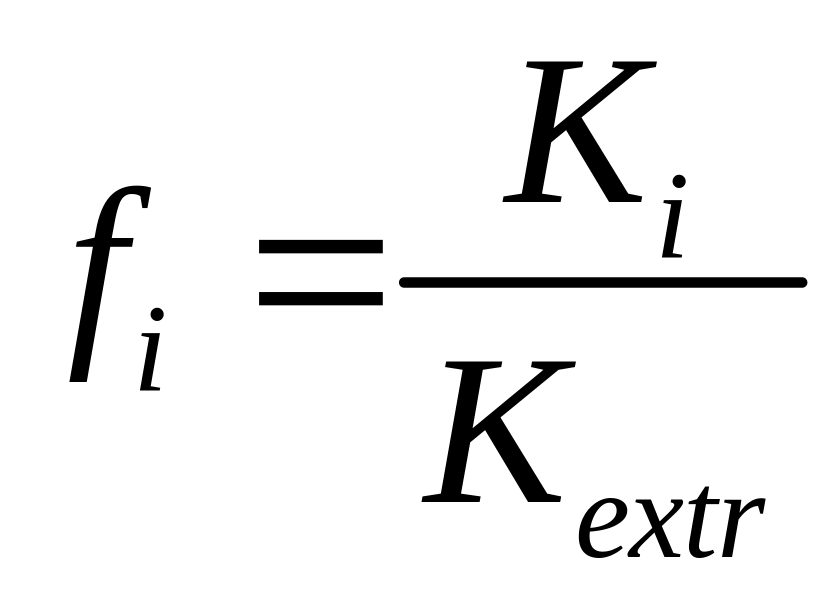
Модель\критерий	G(fi)	V(fi)	H(fi)	C(fi)	Y(fi)
N1	2,75	1	1	1,5	0,4
N2	3,13	0,5	0,64	1,65	1
N3	1	1	1	2,15	0,6
N4	1,32	1	1	1,63	0,2
N5	1,15	0,5	1	1	0,8

11. Выбор вида обобщенного критерия

Выбор будем осуществлять по двум обобщенным критериям: метрическому и аддитивному.

12. Выбор наилучшего результата

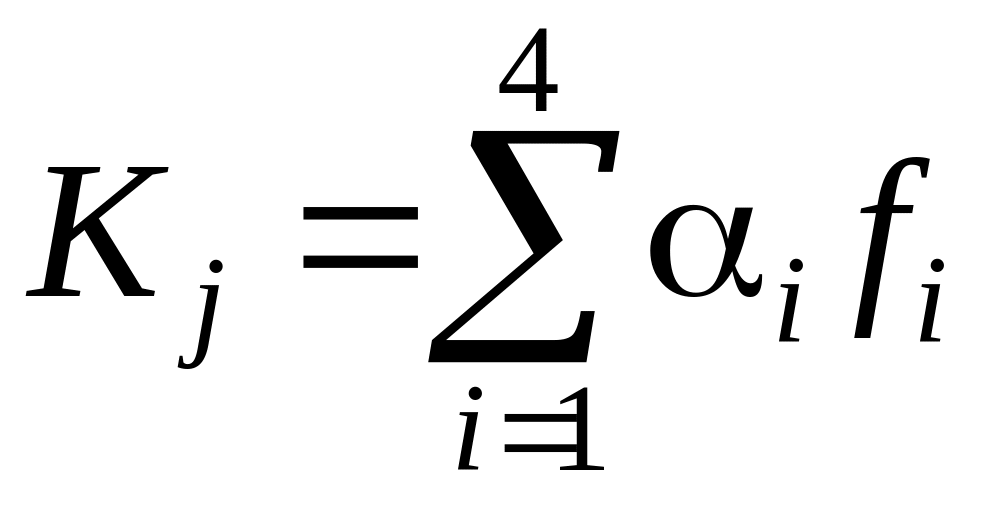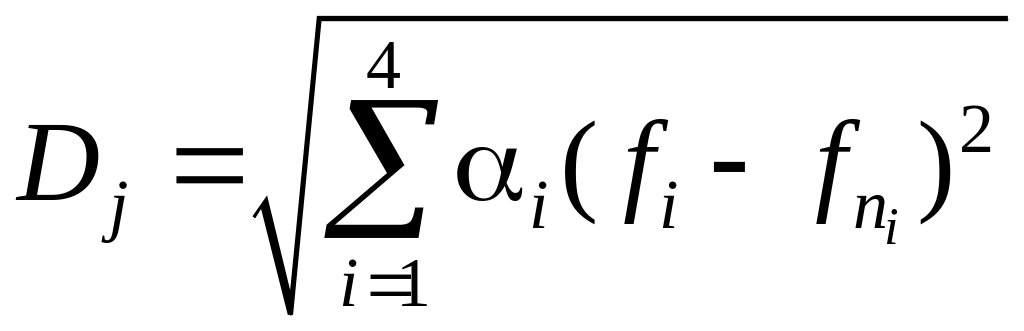, j = 1…4

, j = 1…4.

j – номер варианта

i – номер критерия

Максимизируемые берутся со знаком +

Минимизируемые берутся со знаком –

Вариант	Dj	Место	Kj	Место
N1	0,7056	4	-0,1421	3
N2	0,7186	5	-0,2752	5
N3	0,6161	3	-0,1265	2
N4	0,5113	2	-0,1795	4
N5	0,2443	1	0,0965	1

Таким образом, лучшим является вариант N5.