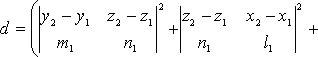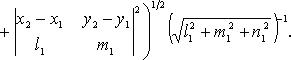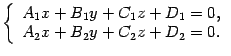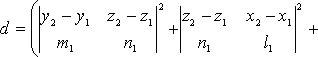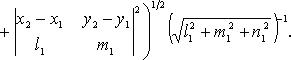8.Прямая в пространстве
Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой принадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.
Итак,
если уравнения двух непараллельных
плоскосте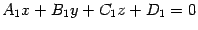й -- 
и 
,
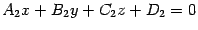то прямая, являющаяся их линией
пересечения, задается системой уравнений
|
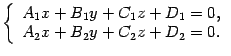
(11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Уравнения (11.11) называют общими уравнениями прямой в пространстве.
В координатах (параметрические уравнения):
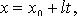
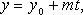
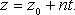
Канонические уравнения прямой
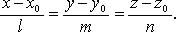
Уравнения прямой по двум точкам
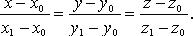
Прямая как линия пересечения двух плоскостей
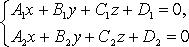
при условии, что не имеют места равенства
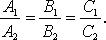
Направляющий вектор такой прямой
Где
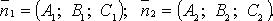
Расстояние между двумя параллельными прямыми
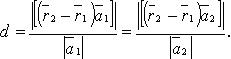
В координатах
