
- •1.Линейные операции над векторами и их свойства.
- •1. Сложение векторов
- •2. Умножение на число
- •3. Свойства линейных операций
- •Теорема
- •2..Базис плоскости.Теорема о базисе плоскости.
- •6.Уравнение прямой на плоскости.
- •Уравнение прямой, проходящей через две точки
- •7.Уравнение плоскости
- •8.Прямая в пространстве
1.Линейные операции над векторами и их свойства.
1. Сложение векторов
Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние.
2. Умножение на число
Произведением
вектора ![]() на
число
на
число ![]() называется
вектор, который:
называется
вектор, который:
коллинеарен вектору ;
сонаправлен ему, если
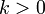 ,
или противоположно направлен, если
,
или противоположно направлен, если 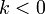 ;
;длины связаны следующим соотношением:
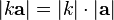 .
.
3. Свойства линейных операций
Сложение векторов коммутативно:
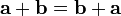 .
.Сложение векторов ассоциативно:
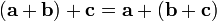 .
.Прибавление нулевого вектора к любому не меняет последнего:
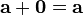 .
Очевидно,
.
Очевидно, 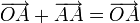 .
.Для любого вектора
 существует
вектор
существует
вектор 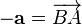 такой,
что
такой,
что 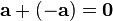 или
или 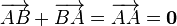 .
.Умножение вектора на число ассоциативно:
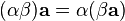 .
Умножение вектора на число дистрибутивно
относительно сложения чисел:
.
Умножение вектора на число дистрибутивно
относительно сложения чисел: 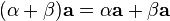 .
.Дистрибутивность умножения векторов относительно сложения: умножение вектора на число дистрибутивно относительно сложения векторов:
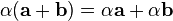 .
.Очевидно, умножение на единицу не меняет вектор:
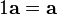
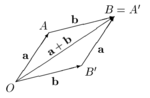 Коммутативность
сложения векторов
Коммутативность
сложения векторов
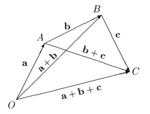 Ассоциативность
сложения векторов
Ассоциативность
сложения векторов
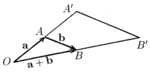 Дистрибутивность
умножения векторов относительно сложения
Дистрибутивность
умножения векторов относительно сложения
Теорема
Система векторов линейно зависима тогда и только тогда, когда один из векторов является линейной комбинацией остальных.
Необходимость. Пусть
система векторов линейно зависима. Это
значит, что существует нетривиальная
линейная комбинация, равная нулю: ![]() .
Один из коэффициентов, например
.
Один из коэффициентов, например ![]() не
равен нулю. Тогда
не
равен нулю. Тогда
![]()
Достаточность. Пусть ![]() .
Тогда
.
Тогда
![]()
Это
нетривиальная (коэффициент ![]() )
линейная комбинация, равная нулю. Значит
система векторов линейно зависима.
)
линейная комбинация, равная нулю. Значит
система векторов линейно зависима.
Геометрический смысл линейной зависимости заключается в следующем:
система из двух векторов линейно зависима тогда и только тогда, когда векторы коллинеарны;
система из трех векторов линейно зависима тогда и только тогда, когда векторы компланарны;
всякие четыре вектора линейно зависимы.
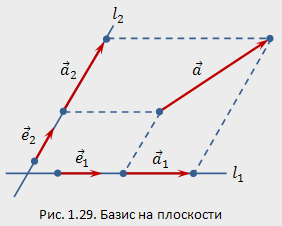
2..Базис плоскости.Теорема о базисе плоскости.
Базисом
на плоскости называются
два неколлинеарных вектора
![]() на
этой плоскости, взятые в определённом
порядке (рис. 1.29). Эти векторы
называются
базисными.
на
этой плоскости, взятые в определённом
порядке (рис. 1.29). Эти векторы
называются
базисными.
Теорема
1.4 (о разложении вектора по базису на
плоскости). Любой
вектор ![]() ,
принадлежащий плоскости, может быть
разложен по базису
на
этой плоскости, т.е. представлен в виде
(1.3), где числа
,
принадлежащий плоскости, может быть
разложен по базису
на
этой плоскости, т.е. представлен в виде
(1.3), где числа ![]() и
и ![]() определяются
однозначно.
определяются
однозначно.
Коэффициенты
и
в
разложении (1.3) называются координатами
вектора
относительно
базиса
(число
называют
абсциссой, а
—
ординатой вектора
).
Например, числа 2 и -3 являются координатами
вектора ![]() (
( ![]() —
абсцисса,
—
абсцисса, ![]() —
ордината вектора
).
—
ордината вектора
).
Базисные векторы , отложенные от одной (произвольной) точки плоскости, называются репером на плоскости.
3.Скалярное произведение векторов. Свойства,приложения.
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается ab,а* b(или( а, b)).Итак, по определению,
Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab=ba

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0 b, то а b
.
Угол между векторами
Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=( bх; bу; bг):
![]()
Отсюда следует условие перпендикулярности ненулевых векторов а и b:
![]()
Проекция вектора на заданное направление
Нахождение
проекции вектора а на
направление, заданное вектором b,
может осуществляться по формуле

4.Векторное произведение векторов, свойства приложения.
Векторным произведением вектора а на вектор b называется вектор с, который:
1. Перпендикулярен векторам a и b, т. е. са и сb;
2. Имеет
длину, численно равную площади
параллелограмма, построенного на
векторах а и b как
на сторонах (см. рис. 17), т. е.
![]()
3.Векторы a, b и с образуют правую тройку.
Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k
Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).
Векторы а х b и b х а коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а, b , а х b и a, b , b x a противоположной ориентации). Стало быть a x b = - (b x a ).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. (а хb ) = (а ) х b = а х (b ).

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.
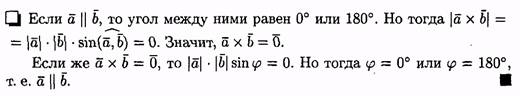
В частности, i *i =j *j =k *k =0.
4. Векторное произведение обладает распределительным свойством:
(a+b) хс= ахс+b хс.
Примем без доказательства.
Некоторые приложения векторного произведения
Установление коллинеарности векторов
![]()
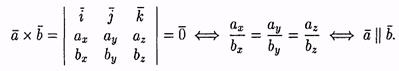
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а| * |b |sin , т. е. S пар = |а х b |. И, значит, S =1/2|а х b |.
5.Смешанное произведение векторов,свойства приложения.
Определение.
Смешанным произведением упорядоченной
тройки векторов
![]() называется
скалярное
произведение
первого
вектора
на
векторное
произведение
второго
вектора
на
третий и обозначается
называется
скалярное
произведение
первого
вектора
на
векторное
произведение
второго
вектора
на
третий и обозначается
![]() .
.
Теорема. (Геометрический смысл смешанного произведения.)
1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
![]() .
.
2) ![]() ,
если тройка
,
если тройка ![]() –
правоориентированная и
–
правоориентированная и ![]() в
противном случае.
в
противном случае.
Доказательство.
1) Обозначим через ![]() объем
параллелепипеда, построенного на данных
векторах, как на его ребрах.
объем
параллелепипеда, построенного на данных
векторах, как на его ребрах.

рис.3.
Объем
параллелепипеда V равен произведению
площади основания S на высоту Н: ![]() .
.
Площадь
основания S численно равна модулю векторного
произведения: ![]() ,
а высота Н равна модулю проекции вектора
,
а высота Н равна модулю проекции вектора ![]() на
вектор
на
вектор ![]() :
:
![]() .
.
Отсюда получаем:
![]() ,
ч.т.д.
,
ч.т.д.
2)
Так как ![]()
![]() ,
где
,
где ![]() ,
то знак смешанного произведениязависит
от угла
,
то знак смешанного произведениязависит
от угла ![]() .
Если он острый, то смешанное
произведение
и
,
если угол
–
тупой. А это зависит, в свою очередь, от
ориентации тройки векторов
.
На рисунке 3 изображена правая тройка
векторов
.
Если смотреть со стороны третьего вектора
.
Если он острый, то смешанное
произведение
и
,
если угол
–
тупой. А это зависит, в свою очередь, от
ориентации тройки векторов
.
На рисунке 3 изображена правая тройка
векторов
.
Если смотреть со стороны третьего вектора ![]() ,
то кратчайший поворот первого вектора
ко
второму
,
то кратчайший поворот первого вектора
ко
второму ![]() осуществляется
против часовой стрелки. В этом
случае угол
–
острый и
.
Если же тройка
–
левая, то конец вектора
будет
лежать нижеплоскости векторов
и
(по
сравнению с рис.3) и угол
будет
тупым и
,
ч.т.д.
осуществляется
против часовой стрелки. В этом
случае угол
–
острый и
.
Если же тройка
–
левая, то конец вектора
будет
лежать нижеплоскости векторов
и
(по
сравнению с рис.3) и угол
будет
тупым и
,
ч.т.д.
Теорема доказана.
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b)•с=(b х с)•а=(с х а)•b .
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).
Действительно, (ахb )•с=±V и а•(b хс)=(b хс)•а=±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации.
Следовательно, (a хb )•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b)с в виде abc без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4.Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны.
Если abc =0 , то а, b и с— компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом V 0. Но так как abc =±V , то получили бы, что abc0 . Это противоречит условию: abc =0.
Обратно, пусть векторы а, b , с — компланарны. Тогда вектор d =ахb будет перпендикулярен плоскости, в которой лежат векторы а, b ,с, и следовательно, d с. Поэтому d •с=0, т. е. abc =0.
Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc >0 , то а , b , с — правая тройка; если abc <0 , то а, b , с - левая тройка.
Установление компланарности векторов
Векторы а, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю
![]()

Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах а, b и с вычисляется как V=|аbс|, а объем треугольной пирамиды, построенной на этих же векторах, равен V =1/6*|abc |.
