Динамические нагрузки.

При решении задач на ударную нагрузку придерживаются следующего порядка расчета:

а) в месте падения груза к упругой системе прикладывают статическую нагрузку, равную весу падающего груза;

б) определяют статическую деформацию упругой системы;

в) определяют напряжения в материале, возникающие от приложения статической нагрузки;

г) определяют коэффициент динамичности;

д) определяют динамические напряжения и деформации.

е) сравнивают напряжения при ударе с допускаемыми

Рассмотрим различные примеры ударного нагружения упругих систем при ударе об них груза , падающего с высоты ;

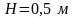Материал упругой системы: Сталь ( ). Массой упругой системы пренебречь. Рычаг в заданиях на скручивающий удар считать абсолютно жестким.

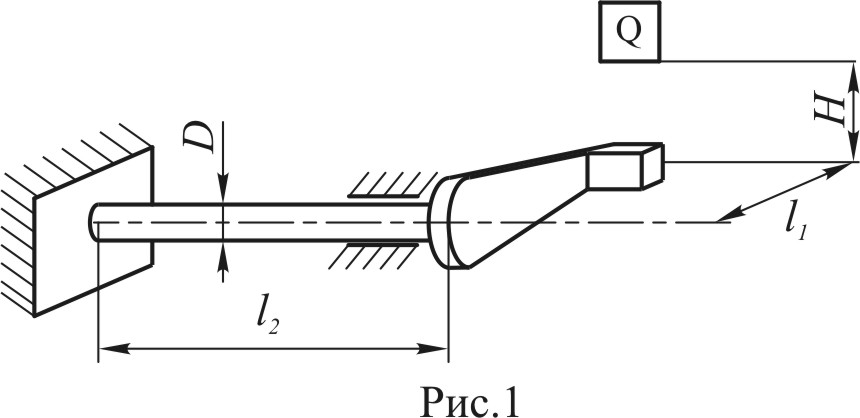
Осевое действие ударной нагрузки.

П усть на ступенчатый стержень квадратного поперечного сечения с высоты падает груз (рис.1).

Стороны квадратного сечения: ; .

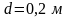Длины участков

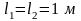
Динамические напряжения в стальном стержне определяются по формуле

,

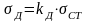где - напряжение, возникающее в материале стержня при воздействии на стержень статически приложенной нагрузки в месте удара.

- коэффициент динамичности.

При статическом приложении нагрузки в месте удара в любом сечении стержня будет возникать продольная сила

.

При этом максимальное напряжение будет в сечениях с меньшей площадью поперечного сечения, т. е. в любом сечении участка с длиной , для которого сторона квадратного сечения равна .

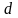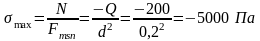
Знак минус указывает на сжимающее нормальное напряжение.

Коэффициент динамичности зависит от высоты падения груза и статической деформации

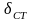
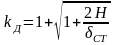
Статическая деформация будет складываться из деформаций участков

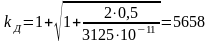
Максимальное динамическое напряжение

Динамическая деформация сечения, в котором прикладывается ударная нагрузка

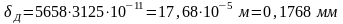
Скручивающий удар.

Пусть стержень, длиной 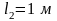и диаметром , испытывает скручивающий удар от нагрузки , падающей с высоты на абсолютно жесткий рычаг длиной 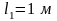. Определим максимальное напряжение и величину перемещения сечения в месте приложения ударной нагрузки.

Предварительно определим статические значения напряжения и перемещения.

Пренебрегая деформацией рычага и полагая, что вследствие малости перемещения проекция на вертикаль перемещения точки соударения равна длине дуги с радиусом 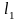, можно вычислить по формуле

,

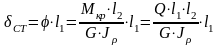где 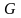- модуль сдвига 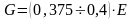. Принимаем ;

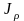- полярный момент инерции. Для круглого поперечного сечения

Коэффициент динамичности

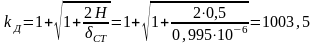
Максимальное статическое напряжение при действии закручивающего момента

.

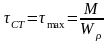- полярный момент сопротивления. Для круглого поперечного сечения

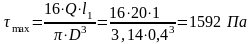
Динамическое напряжение

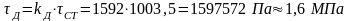
Динамическое перемещение

Изгибающий удар.

П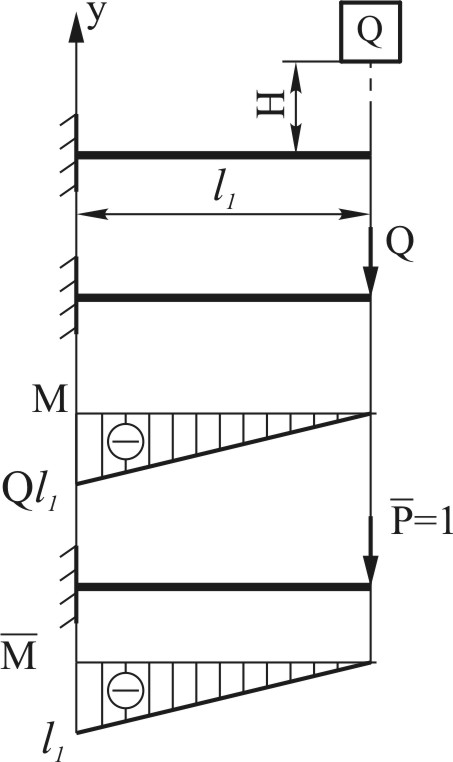 усть на свободный конец консольной балки длиной прямоугольного поперечного сечения с шириной сечения 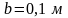и высотой сечения падает груз с высоты .

Определим максимальное напряжение и величину перемещения сечения в месте приложения ударной нагрузки.

Статическое перемещение определим способом Верещагина

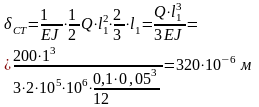
Коэффициент динамичности

Максимальное статическое напряжение будет возникать в опорном сечении

Динамическое напряжение

Динамическое перемещение