Построение эпюр внутренних усилий, напряжений и деформаций при изгибе.
Проверить
прочность и жёсткость консольной балки
с заданными исходными данными (рис.3.2),
если 
, 
Построить
эпюру нормальных напряжений в опасном
сечении балки.
1. Расчетная
схема консольной балки, эпюры 
, MX и
эпюра прогибов.
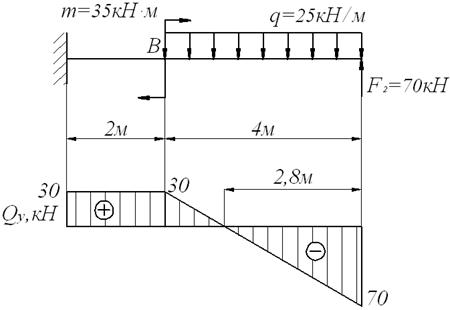
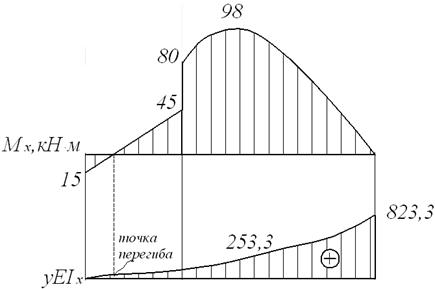
Для строительных специальностей эпюру моментов строим со стороны растянутых волокон.
2. Выписываем из сортамента необходимые данные для швеллера №27:
h = 270мм; b = 95мм; A1 = 35,2см2; = 4160см4; = 2,47см.
3. Вычерчиваем заданное сечение в масштабе (рис.3.4).
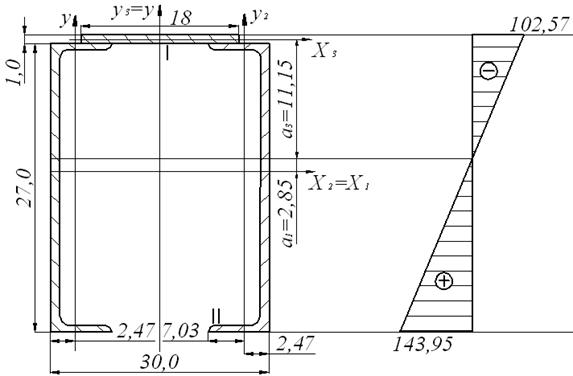
Поперечное сечение и эпюра нормальных напряжений
4. Определяем координаты центра тяжести сечения относительно осей х1, у1.
Проводим оси х, у — главные центральные оси сечения.
5. Определяем осевой момент инерции заданного сечения.
6. Определяем нормальные напряжения в наиболее удалённых от оси х точка сечения I и II (по чертежу находим у1=11,65см, у2=-16,35см).
7. Проверяем прочность балки.
,
прочность обеспечена.
8. Составляем универсальное уравнение изогнутой оси балки.
Начальные параметры:
у0 = у0' = 0; М0= - 15кН•м; Q0 = 30кН.
9. Вычисляем прогибы балки в точках В, С, D.
;
;
10. Проверяем жёсткость балки.
Жесткость балки не обеспечена.
Расчет шарнирной балки на прочность и жесткость
1. Вычисляем опорные реакции (рис.3.5).
2. Строим эпюры QY и MX .
Расчетная схема балки и эпюра
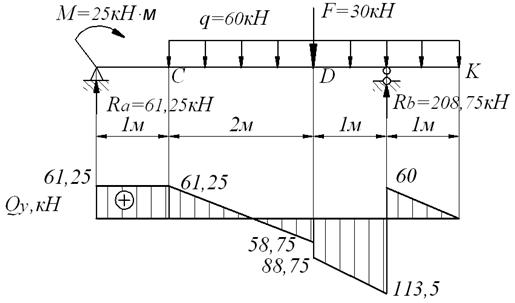
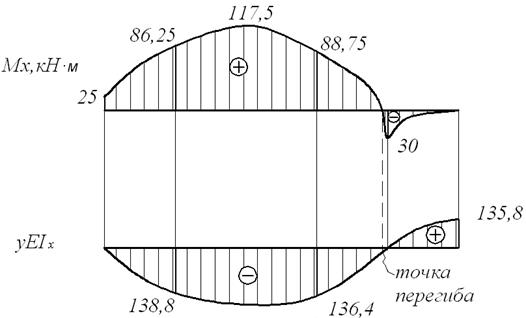
Эпюра изгибающих моментов и прогибов
Для строительных специальностей эпюру моментов строим со стороны растянутых волокон.
3. Подбираем три вида поперечных сечений по условию прочности.
По сортаменту выбираем двутавр №36
Для прямоугольного сечения при h = 3b
Для круглого сечения:
Веса балок относятся друг к другу как их площади поперечных сечений:
следовательно, рациональным является двутавровое сечение.
4. Составляем универсальное уравнение изогнутой оси балки.
Начальные параметры:
Угол поворота y0' определяем из условия:
5. Вычисляем прогибы балки в точках С, D, К.
6. Подбираем двутавровое сечение по условию жёсткости.
Требуемый момент инерции:
По сортаменту выбираем двутавр №33:
Окончательно, по условиям прочности и жёсткости, принимаем двутавр №36.
7. Строим эпюры нормальных и касательных напряжений.
Выписываем из сортамента для двутавра №36:
h = 360мм; b = 145мм; d = 7,5мм; t = 12,3мм; Ix = 13380см4; Wx = 743см3; Sx = 423см3.
Касательные напряжения в характерных точках сечения определяем по формуле Журавского:
Эпюры 
и 
представлены
на рисунке.
Эпюры нормальных и касательных напряжений
Расчет плоских рам.
Ось
рамы представляет собой ломаную линию,
однако каждый прямолинейный участок
ее можно рассматривать как балку.
Поэтому, чтобы построить какую либо
эпюру для рамы, нужно построить ее для
каждой отдельной балки, входящей в
состав рамы. В
отличие от обыкновенных балок в сечениях
стержней рамы, кроме изгибающих
моментов М и поперечных сил Q, обычно
действуют еще и продольные силы N.
Следовательно, для рам нужно строить
эпюры
,
и
.
Для и сохраняются ранее принятые правила знаков:
,
если продольные силы вызывают растяжение;
,
если ее векторы стремятся вращать части
рассеченной рамы (относительно центра
тяжести сечения) по часовой стрелке.
Для
изгибающего момента специального
правила знаков не устанавливают, а при
установлении выражений для
выбирают произвольно направление
положительного момента.
Выражения
для
,
,
и
записывают очень редко — главным образом
для тех участков, где действует
распределенная нагрузка. Чаще всего
просто вычисляют значения
,
и
в характерных сечениях (на границах
участков и в экстремальных точках), а
затем проводят линии эпюр, учитывая
особенности построения этих эпюр.
Ординаты эпюр, как и всегда, откладываем перпендикулярно к оси рамы, причем положительные ординаты и с внешней стороны рамы, а отрицательные — с внутренней (если, конечно, рама такой конфигурации, что можно различить ее наружную и внутреннюю стороны). Эпюры М условимся и для рам строить на сжатых волокнах.
Рассмотрим пример построения эпюр внутренних силовых факторов для плоской рамы (рис. 1), нагруженной следующей нагрузкой:
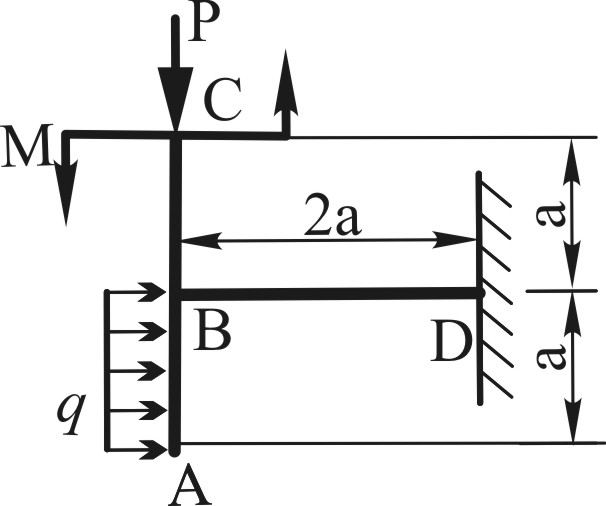
рис. 11
М = 20 кН·м; q = 10 кН/м; Р = 15 кН; а = 1,0 м;
Чтобы построить эпюру N необходимо спроецировать силы, приложенные к части рамы, лежащие по одну сторону от сечения, на ось стержня. Таким образом:
1участок (АВ) – N(х1) = 0; (1)
2участок (СВ) – N(х2) = -Р = -15 кН; (2)
3участок (ВD) – N(х3) = -q·а = -10 кН. (3)
По этим данным строим эпюру N (рис 2)
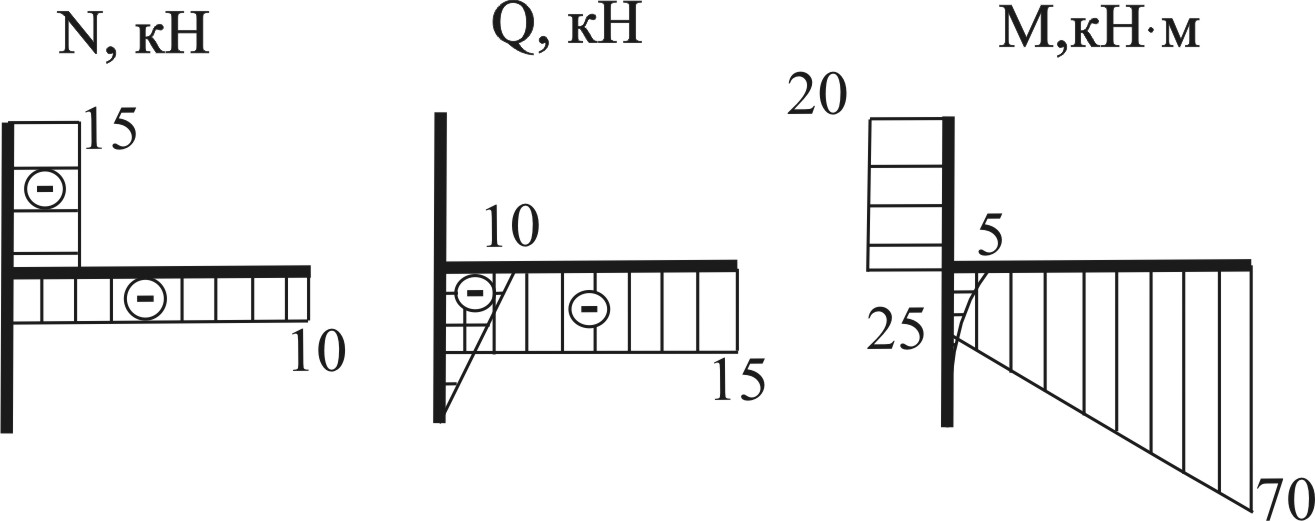
рис. 12
Перейдем к построению эпюры Q.
На участке АВ линейная зависимость поперечной силы от координаты х1:
(4)
Для точки А (х1 = 0)
кН
Для точки В (х1 = а)
кН
На втором участке СВ для любого сечения сумма проекций вышележащих сил на поперечную ось равна нулю
кН (5)
На участке BD для любого сечения сумма проекций всех лежащих слева сил на поперечную ось сечения одинакова, равна Р и дает отрицательную величину поперечной силы
кН (6)
Для построения эпюры откладываем на участке АВ значения поперечной силы в сечении А и В и соединяем две точки прямой линией. На участках CВ и BD эпюра представлена двумя прямоугольниками.
Поскольку значения поперечной силы на участке АВ не меняет своего знака, то для построении эпюры моментов вычисляем значение изгибающих моментов в характерных сечениях А, В, С, D:
для первого участка АВ
кН·м (7)
кН·м (8)
для второго участка СВ
кН·м (9)
кН·м (10)
для третьего участка BD
кН·м (11)
кН·м (12)
Эпюру моментов строим на сжатых волокнах. Для строительных специальностей эпюру моментов строим со стороны растянутых волокон.