МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ

Факультет агротехники и энергообеспечения

Кафедра инженерной графики и механики

КОНСПЕКТ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

По дисциплине «Сопротивление материалов»

Разработал старший преподаватель

Волкова И.Л.

ОРЕЛ-2012

Оглавление:

1. Напряжения и деформации при растяжении_______________________3

2. Расчеты на прочность_______________________________________8

3. Геометрические характеристики плоских сечений________________8

4. Расчет вала на прочность и жесткость при кручении______________10

5. Построение эпюр внутренних усилий, напряжений и деформаций при изгибе____________________________________________________18

6. Расчет балок при косом изгибе_______________________________28

7. Расчет вала на совместное действие изгиба и кручения___________40

8. Расчет стержней при внецентренном сжатии-растяжении__________44

9. Расчет статически неопределимой рамы методом сил_____________48

10. Расчеты на устойчивость_______________________________53

11. Динамические нагрузки________________________________58

12. Список литературы___________________________________63

Напряжения и деформации при растяжении Расчет статически неопределимых стержней при растяжении (сжатии).

Статически неопределимыми называются такие конструкции, в элементах которых при помощи только одних уравнений статики определить усилия невозможно. Например, на рис.1.1 показан ступенчатый стержень, жестко закрепленный в точках и . На стержень действуют силы и . Модуль продольной упругости материала стержня . Площади поперечных сечений участков: ; ; Длина участка . Необходимо раскрыть статическую неопределимость, определить продольные усилия, возникающие в различных частях стержня, нормальные напряжения и перемещения различных точек стержня при заданной нагрузке.

РЕШЕНИЕ:

Заменим действие опор на стержень реакциям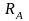и ( и ) и составим уравнение проекций сил на ось стержня (ось ):

; , (1.1)

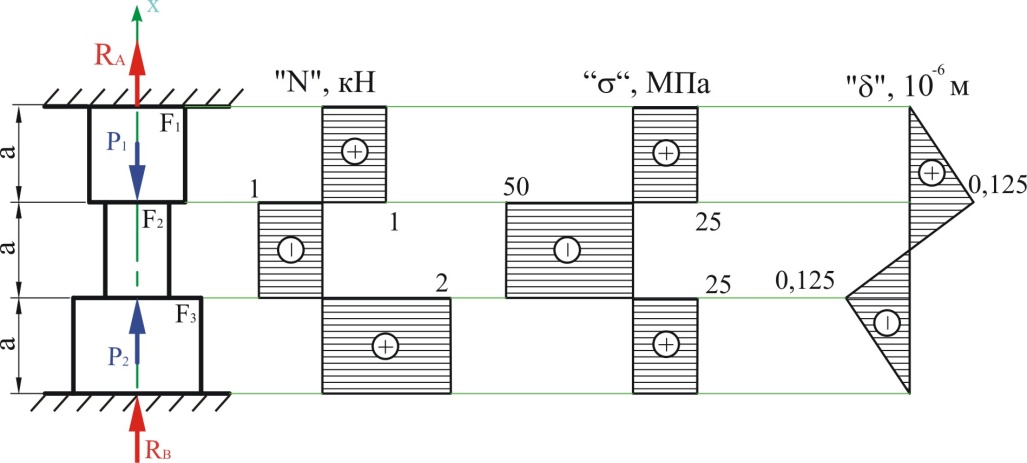
Рис. Ошибка! Текст указанного стиля в документе отсутствует..1

В одно уравнение входят два неизвестных усилия ( и ), следовательно, задача один раз статически неопределима.

Для расчета таких систем необходимо составить дополнительное уравнение. Таким уравнением служит – уравнение деформации. Так как концы стержня жестко закреплены, то общая длина не изменяется:

.

Общая деформация стержня будет складываться из деформаций его элементов:

, (1.2)

где – продольное усилие на -том участке;

– длина - того участка;

– модуль продольной упругости материала;

– площадь поперечного сечения - того участка.

Выразим продольные усилия в поперечных сечениях стержня через одну из неизвестных реакций .

Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка (рис. 1.1).

Мысленно рассечем первый участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой , которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 1.2).

Рис. Ошибка! Текст указанного стиля в документе отсутствует..2

Из условия равновесия: 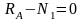; (1.3)

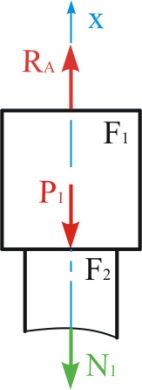
Рис. Ошибка! Текст указанного стиля в документе отсутствует..3

Мысленно рассечем второй участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 1.3).

Из условия равновесия:

;

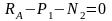(1.4)

Для третьего участка (рис. 1.3):

;

(1.5)

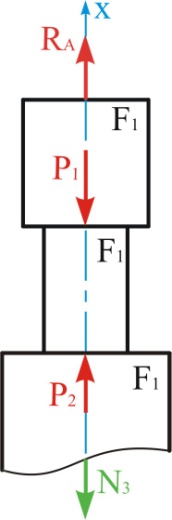
Рис. Ошибка! Текст указанного стиля в документе отсутствует..4

Деформация участков согласно ф-ле (1.2):

(1.6)

(1.7)

(1.8)

Общая деформация должна равняться нулю:

Умножив обе части уравнения на получим:

,

или:

.

Из выражения (1.1):

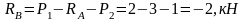(1.8)

Знак «-» указывает на обратное направление реакции _.

Определяем значения осевых усилий для каждого участка по найденным ранее выражениям (1.3.) – (1.5):

;

;

.

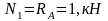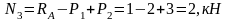По полученным значениям строим эпюру осевых усилий. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.1). В одну сторону откладываем положительные значения, в другую - отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («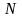 ») и через запятую - единицы измерения ( ).

Нормальные напряжения в поперечных сечениях:

(1.8)

;

;

.

По полученным значениям нормальных напряжений строим эпюру нормальных напряжений (« ») (рис. 1.1).

Определим деформацию каждого участка:

;

;

.

Эпюру перемещений строим по перемещениям точек , , , .

Сечение в точке возьмем как базовое, перемещение которого . Тогда перемещение точки будет равно удлинению первого участка:

Перемещение точки будет складываться из перемещения точки и удлинения второго участка:

Перемещение точки будет складываться из перемещения точки и удлинения второго участка:

Перемещение является своего рода проверкой правильности решения данной задачи, так как точка принадлежит неподвижной опоре.

По полученным значениям строим эпюру перемещений (« ») (Рис. 1.1).

Так как внутри участков перемещения поперечных сечений имеют пропорциональную зависимость от координаты сечения , значения, отложенные в точках , , , , соединяются между собой прямыми линиями.