Уравнение массоотдачи

В практических расчетах принимают, что количество вещества, переносимого в единицу времени в каждой из фаз, пропорционально разности концентраций в ядре и на границе фазы либо на границе фазы и в ядре потока.

Основное уравнение массоотдачи выражается следующим образом:

для фазы Ф_у

(3.20)

для фазы Ф_x

(3.21)

здесь - коэффициент массоотдачи в жидкой среде;

- коэффициент массоотдачи в газовой среде.

Они показывают, какое количество вещества переходит от поверхности раздела фаз в ядро фазы (или в обратном направлении) через единицу поверхности в единицу времени при движущей силе, равной единице. Коэффициент является функцией многих переменных, т.е.

(физические свойства среды, , , геометрических параметров и др.)

Подобие процессов массоотдачи

Принципиальный путь для определения коэффициентов массоотдачи заключается в интегрировании уравнения диффузии в движущейся среде (3.19) совместно с уравнениями движения Навье-Стокса и уравнением неразрывности потока при заданных начальных и граничных условиях. Однако система указанных уравнений практически не имеет общего решения. В этом случае на основе теории подобия можно найти связь между переменными, характеризующими процесс переноса в потоке фазы, в виде критериального уравнения массоотдачи.

Подобие граничных условий можно установить, допуская наличие пограничного слоя, в котором перенос осуществляется только молекулярной диффузией. Количество вещества, переходящего из ядра фазы Ф_у к границе фазы Ф_x (рисунок 3.5), в соответствии с уравнением (3.20) составляет:

То же количество вещества переносится молекулярной диффузией через пограничный слой при

Приравняв эти два выражения, найдем зависимость, характеризующую подобие условий переноса на границе фазы:

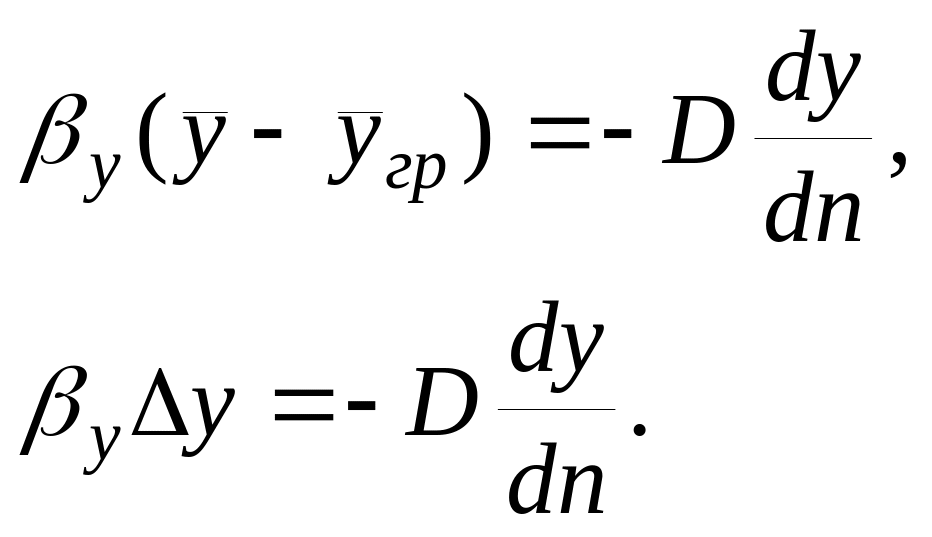
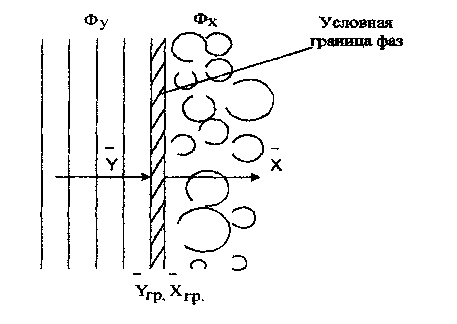
Рисунок 3.5 – Схема переноса вещества из фазы Ф_y в фазу Ф_x

Учитывая, что для подобных процессов отношение сходственных величин равно отношению величин им пропорциональным, дифференциалы заменим конечными разностями:

В соответствии с правилом преобразования дифференциальных уравнений разделим левую часть уравнения на его правую часть, сократим подобные члены и опусти знак «d» для подобных систем, тогда получим:

Выражение (3.22)

Комплекс (3.22) представляет собой критерий подобия и носит название диффузионного критерия Нуссельта ( )

(3.23)

где - мера интенсивности суммарного переноса вещества в фазе;

- мера интенсивности переноса молекулярной диффузии;

- выражает подобие переноса вещества у границы фазы в рассматриваемых системах.

Таким образом, можно считать, что выражает отношение интенсивности переноса в ядре фазы к интенсивности переноса в диффузионном пограничном подслое, где она определяется молекулярной диффузией. При рассмотрении подобных процессов переноса вещества в качестве исходной зависимости используется дифференциальное уравнение (3.19) и путем поочередного деления левой части этого уравнения на правую, можно прийти к общей функциональной зависимости от определяющих критериев и симплексов подобия. Для установившегося процесса массоотдачи критерий выражается зависимостью

(3.24)

где - критерий Рейнольдса; - критерий Прандтля; - критерий Галилея; - геометрические характеристики:

Зависимость (3.24) может быть представлена в степенной форме:

В развернутом виде можно записать:

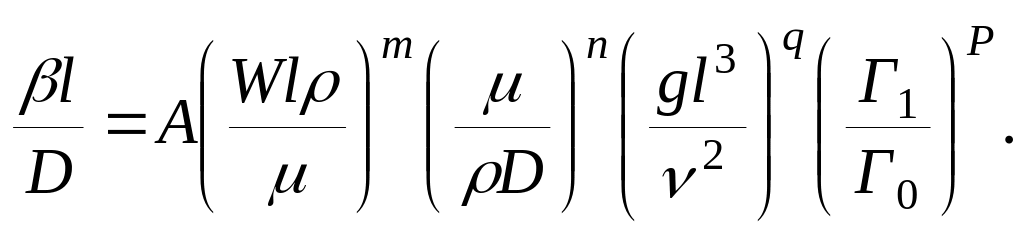(3.25)

Зависимость (3.25) называется обобщенным критериальным уравнением массоотдачи. Численное значение входящего в него коэффициента А и показателей степени m, n, q, p находят обработкой опытных данных.