Уравнение Бернулли

Взяв систему уравнений движения Эйлера, умножив левые и правые части каждого из уравнений соответственно на dx, dy, dz и разделив на плотность  жидкости, получим:

.

Сложим эти уравнения, учитывая, что производные , , выражают проекции W_x, W_y и W_z скорости на соответствующие оси координат. Тогда получим

.

Cлагаемые левой части уравнения могут быть представлены в виде:

, , .

Следовательно, их сумма равна

,

где W= |W| – величина вектора скорости, составляющие которой вдоль соответствующих осей равны W_x, W_y, W_z.

В то же время сумма членов, стоящих в скобках в правой части записан-ного уравнения, представляет собой полный дифференциал давления dP. Значит,

.

Разделим обе части уравнения на g и перенесём все слагаемые в левую часть:

.

Для жидкости  = const.

Сумма дифференциалов может быть заменена дифференциалом суммы,

следовательно:

,

откуда . (2.56)

Уравнение (2.56) для любых двух поперечных сечений 1 и 2 потока можно представить в виде:

. (2.57)

Для горизонтального трубопровода .

Уравнение (2.57) является уравнением Бернулли для идеальной жидкости.

Величину называют полным гидродинамическим напором или просто гидродинамическим напором.

Согласно уравнению Бернулли для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

Величина Z называется геометрическим напором или нивелирной высотой (h_г) (входила в уравнение гидростатики).

Величина P/g - гидростатический или пьезометрический напор (h_ст) - характеризует потенциальную энергию давления в данном сечении.

Величина W ²/ 2g - скоростной или динамический напор (h_ск).

Уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.

Если умножить левую и правую часть уравнения (2.57) на , то оно может быть представлено в виде:

. (2.58)

Уравнение (2.58) выражает удельную энергию в данной точке, отнесенную не к единице массы, а к единице объема жидкости (1 м³).

Х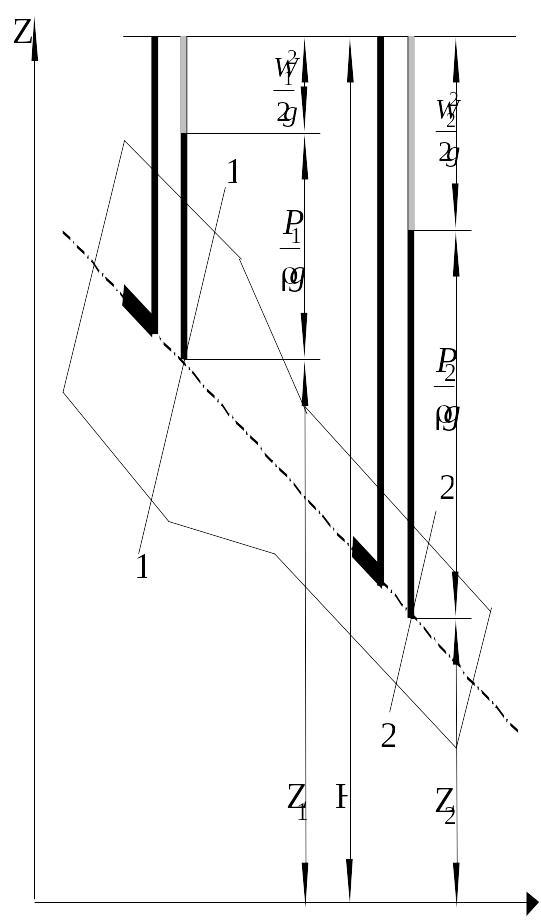

Рисунок 2.14 - Иллюстрация уравнения Бернулли для идеальной жидкости

Иллюстрация применения уравнения Бернулли на примере потока идеальной жидкости, движущейся через произвольно расположенный в пространстве трубопровод переменного сечения, показана на рисунке 2.14.

Для реальной жидкости справедливо неравенство:

При движении реальной жидкости высоты ее подъема (относительно плоскости сравнения) в трубках с концами, обращенными навстречу потоку, не будут равны в сечениях 1-1 и 2-2. Разность высот в этих трубках, обусловленная потерями энергии на пути жидкости от сечения 1-1 до сечения 2-2, характеризует потерянный напор.

Уравнение Бернулли для реальной жидкости имеет вид:

, (2.59)

где h_n - характеризует удельную (отнесенную к единице массы жидкости) энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

Если умножить обе части уравнения (2.59) на g, то найдем

, откуда .

Определение Р является одной из важных задач при проектировании пылегазоочистных установок.