Уравнение плоскости в пространстве. У равнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

Пусть в прост-ве Оxyz пл-ть Q задана точкой М₀(х₀;у₀;z₀) и вектором , который называется нормальным вектором пл-ти, перпендикулярным этой плоскости. Возьмем на пл-ти Q произвольную точку М(х;у;z) и составим вектор .

При любом расположении точки М на пл-ти векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю, т.е.

Общее уравнение плоскости.

Общее уравнение первой степени с тремя переменными х, у и z, имеет вид:

Частные случаи:

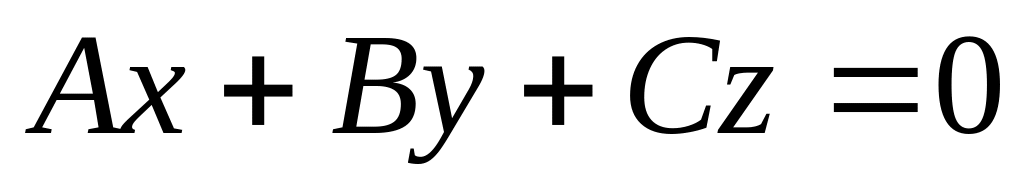
1. Если D=0, то оно принимает вид  пл-ть проходит через начало координат;

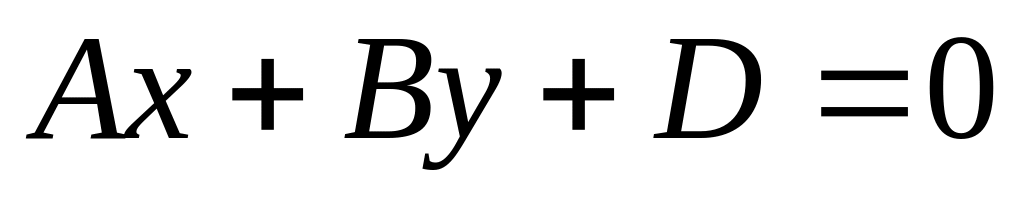
2. Если С=0, то имеем ур-ние  пл-ть параллельна оси Oz;

Если В=0, то имеем ур-ние  пл-ть параллельна оси Oу;

Если А=0, то имеем ур-ние  пл-ть параллельна оси Oх;

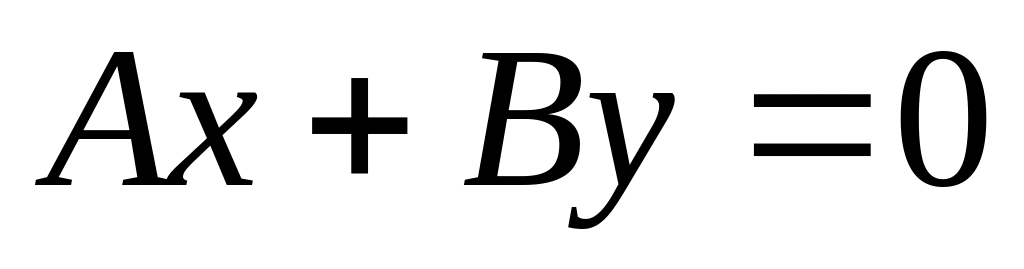
3. Если C=D=0, то имеем ур-ние  пл-ть проходит через ось Oz;

Если А=D=0, то имеем ур-ние  пл-ть проходит через ось Oх;

Если В=D=0, то имеем ур-ние  пл-ть проходит через ось Oу;

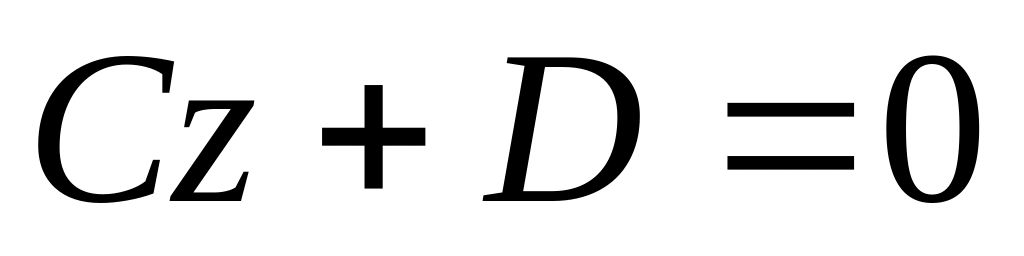
4. Если А=В=0, то имеем ур-ние  пл-ть параллельна пл-ти Оху;

Если В=С=0, то имеем ур-ние  пл-ть параллельна пл-ти Оуz;

Если А=С=0, то имеем ур-ние  пл-ть параллельна пл-ти Охz;

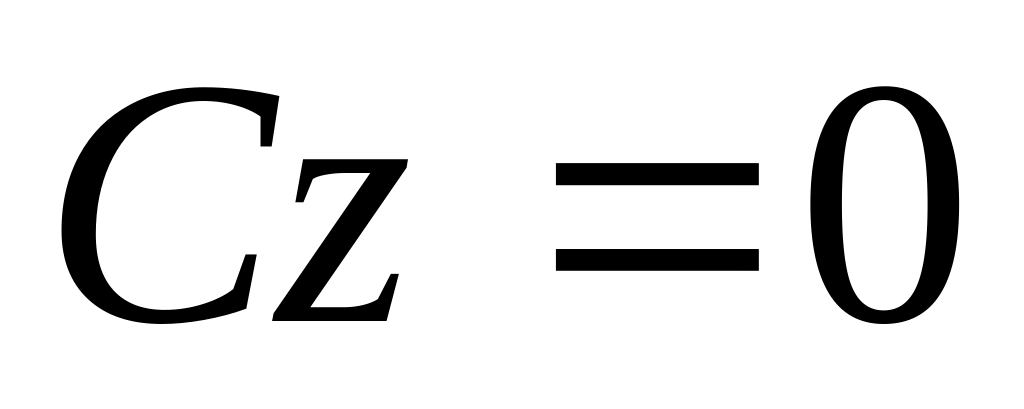
5. Если А=В=D=0, то имеем ур-ние  это ур-ние пл-ти Оху;

Если А=С=D=0, то имеем ур-ние  это ур-ние пл-ти Охz;

Если В=С=D=0, то имеем ур-ние  это ур-ние пл-ти Оуz.

Уравнение плоскости, проходящей через три дванные точки.

Пусть даны три точки М₁(х₁; у₁; z₁), M₂(x₂; y₂; z₂) и M₃(x₃; y₃; z₃), не лежащие на одной прямой. Возьмем на плоскости произвольную точку М(х; у; z) и составим векторы: , , . Эти векторы лежат на плоскости, следовательно, они компланарны. Используя условие компланарности, получаем:

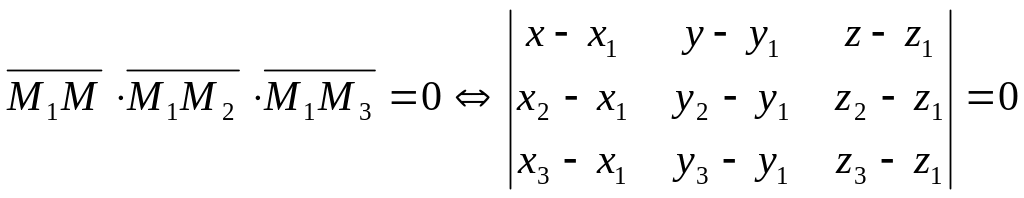
Следствия:

1. Если дана точка М₁(х₁; у₁; z₁) и два направляющих вектора 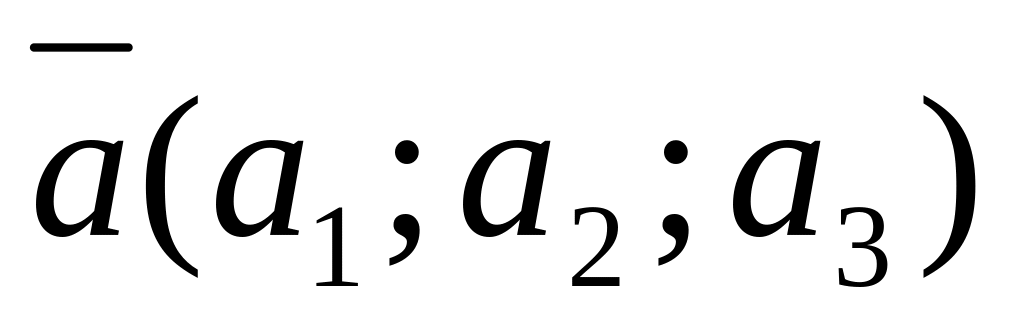и 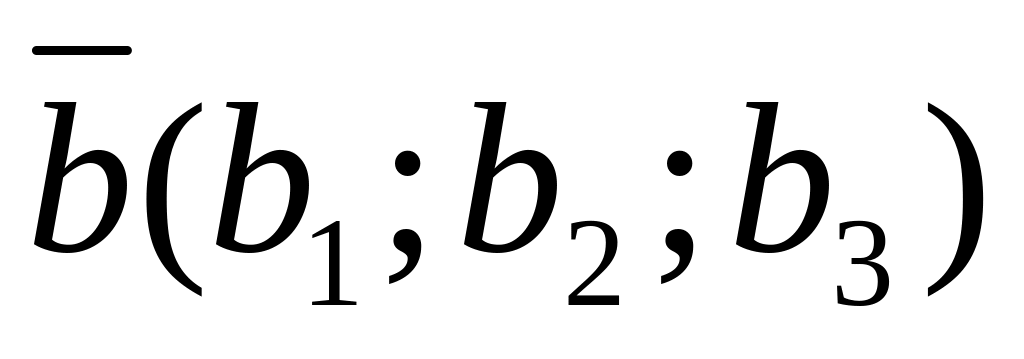, то уравнение плоскости задается следующим образом: .

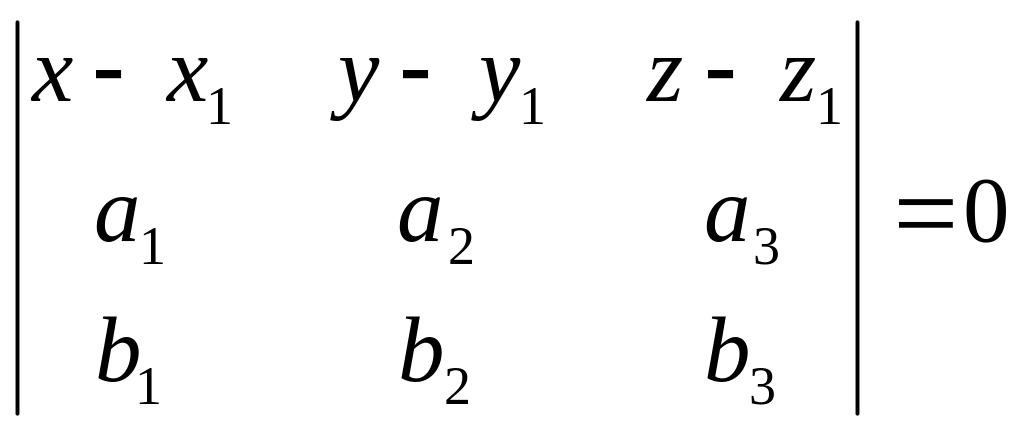2. Если даны две точки М₁(х₁; у₁; z₁), M₂(x₂; y₂; z₂) и направляющий вектор , то уравнение плоскости задается следующим образом: .

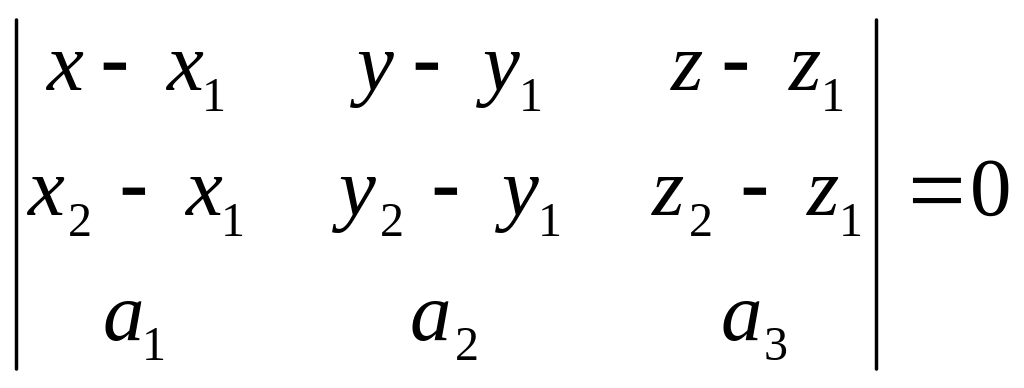Уравнение плоскости в отрезках.

П усть пл-ть отсекает на осях Ох, Оу и Оz соответственно отрезки a, b и c, т.Е. Проходит через точки а(а,0,0), в(0,b,0) и с(0,0,с). Подставляя координаты этих точек в ур-ние, получаем:

. Раскрыв определитель и выполнив преобразования, имеем:

Нормальное уравнение плоскости.

П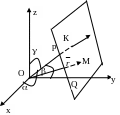 оложение плоскости Q определяется заданием единичного вектора , имеющего направление перпендикуляра ОК, опущенного на пл-ть из начала координат, и длиной p этого перпендикуляра.

Пусть ОК=р, а , ,  - углы, образованные единичным вектором с осями. Тогда =(cos,cos,cos). Возьмем на пл-ти произвольную точку М(х;у;z) и соединим ее с началом координат.

При любом положении точки М на пл-ти Q проекция радиус-вектора на направление вектора всегда равно р: , т.е. .

Зная координаты векторов и , урвнение можно записать так:

Каноническое уравнение прямой.

Пусть - направляющий вектор прямой L и M₀(x₀;y₀;z₀) – точка, лежащая на этой прямой. Вектор , соединяющий точку М₀ с произвольной точкой М(х;у;z) прямой L, параллелен вектору . Поэтому координаты вектора и вектора пропорциональны: