
- •Лабораторная работа №1. Графическое представление выборки.
- •Лабораторная работа №2. Числовые характеристики выборочного распределения.
- •Лабораторная работа №3. Проверка гипотезы о нормальном законе распределения по критерию согласия Пирсона.
- •Лабораторная работа №4 Интервальные оценки числовых характеристик случайных величин.
- •Лабораторная работа 5 Выборочные характеристики двумерного случайного вектора.
- •Лабораторная работа №6 Линейный регрессионный анализ.
- •Литература.
- •Содержание
Лабораторная работа 5 Выборочные характеристики двумерного случайного вектора.
Цель работы. Вычисление точечных и интервальных оценок числовых характеристик двумерного случайного вектора.
1.
Краткие теоретические.
Пусть
 ,
выборкой
объёма n
из
наблюдений двумерной случайной величины
,
выборкой
объёма n
из
наблюдений двумерной случайной величины
 .
Предварительное представление о
зависимости между X
и Y
можно получить изображая элементы
выборки
.
Предварительное представление о
зависимости между X
и Y
можно получить изображая элементы
выборки
 точками
на плоскости в декартовой системе
координат. Это представление выборок
называется диаграммой рассеивания.
Распределение двумерной выборки
называется распределение двумерного
дискретного случайного вектора,
принимающего значения
точками
на плоскости в декартовой системе
координат. Это представление выборок
называется диаграммой рассеивания.
Распределение двумерной выборки
называется распределение двумерного
дискретного случайного вектора,
принимающего значения
 с вероятностями, равными 1/n.
Распределение
характеризует следующие параметры:
с вероятностями, равными 1/n.
Распределение
характеризует следующие параметры:
 и
и
 случайных
величин X
и Y
определяют положение центра
случайных
величин X
и Y
определяют положение центра
 распределения;
и
распределения;
и
 определяют рассеивание распределения
относительно центра; оценка коэффициента
корреляции
определяют рассеивание распределения
относительно центра; оценка коэффициента
корреляции
 определяет
степень линейной зависимости между X
и Y.
определяет
степень линейной зависимости между X
и Y.
Примеры различных видов рассеивания распределения относительно центра. |
|
|
|
Рисунок 3 |
Рисунок 4 |
Рассеивание распределения относительно центра на рисунке 3 меньше, чем на рисунке 4.
Примеры различных видов корреляции |
|
|
|
|
|
Рисунок 5 |
|
а) предельная линейная корреляция |
b) линейная корреляция с умеренным рассеиванием |
c) нелинейная корреляция |
d) отсутствие корреляции |
Выборочные средние, дисперсии, коэффициент корреляции находятся по формулам:

Выборку
большого объёма представляют в виде
корреляционной таблицы. (Таблица 2). С
этой целью группируют реализации X
и Y
по интервалам длины
 и
и
 ,
а клетки таблицы записывают число пар
,
а клетки таблицы записывают число пар
исходной
выборки для каждой комбинации интервалов.
(Таблица 2). Если вектор
имеет нормальное распределение, то
интервальные оценки
 и
и
 вычисляются по тем же формулам, что и
для одномерных случайных величин.
Доверительные интервалы для коэффициентов
корреляции. При вычислении доверительного
интервала для коэффициента корреляции
вычисляются по тем же формулам, что и
для одномерных случайных величин.
Доверительные интервалы для коэффициентов
корреляции. При вычислении доверительного
интервала для коэффициента корреляции
 используется статистика
используется статистика
 ,
имеющая приблизительно нормальное
распределение
,
имеющая приблизительно нормальное
распределение
 .
Доверительный интервал для
.
Доверительный интервал для
 имеет вид:
имеет вид:
 (1).
(1).
2.
Задание.
Вычислить оценки среднего
,
дисперсии
 и коэффициента корреляции
и коэффициента корреляции
 двумерного случайного вектора. Вычислить
90% доверительный интервал для коэффициента
корреляции.
двумерного случайного вектора. Вычислить
90% доверительный интервал для коэффициента
корреляции.
3. Порядок выполнения задания.
3.1.
Составить и заполнить таблицу 6. Для
упрощения вычисления вместо середин
интервалов
 ввести числа
ввести числа
 ,
где
,
где
 - середины наиболее часто встречающихся
интервалов
- середины наиболее часто встречающихся
интервалов
 =17,5;
=17,5;
 =75.
Вычислить следующие суммы:
=75.
Вычислить следующие суммы:
|
- сумма j-го столбца корреляционной матрицы |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
- сумма i-го столбца корреляционной матрицы |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
- где N-корреляционная матрицы. |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
95 |
90-100 |
85 |
80-90 |
75 |
70-80 |
65 |
60-70 |
55 |
50-60 |
45 |
40-50 |
Границы и середины интервалов для y |
Таблица 6 |
|
|
|
||||||||||||||||
|
|
|
2 |
1 |
0 |
-1 |
-2 |
-3 |
|
|
|
||||||||||||||||||||||||
27 |
-9 |
3 |
0 |
0 |
0 |
0 |
2 |
1 |
-3 |
|
2,5 |
0-5 |
Границы и середины интервалов для x |
|
|
|
|
||||||||||||||||||
29 |
-14 |
7 |
0 |
0 |
0 |
2 |
3 |
2 |
-2 |
7,5 |
5-10 |
|
|
|
|
|
|||||||||||||||||||
18 |
-18 |
18 |
0 |
0 |
1 |
13 |
3 |
1 |
-1 |
12,5 |
10-15 |
|
|
|
|
|
|||||||||||||||||||
0 |
0 |
22 |
0 |
2 |
16 |
4 |
0 |
0 |
0 |
17,5 |
15-20 |
|
|
|
|
|
|||||||||||||||||||
8 |
8 |
8 |
2 |
3 |
3 |
0 |
0 |
0 |
1 |
22,5 |
20-25 |
|
|
|
|
|
|||||||||||||||||||
8 |
4 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
2 |
27,5 |
25-30 |
|
|
|
|
|
|||||||||||||||||||
89 |
-29 |
60 |
4 |
5 |
20 |
19 |
8 |
4 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
-34 |
8 |
5 |
0 |
-19 |
-16 |
-12 |
|
|
|
|
|
||||||||||||||||||||||
|
|
108 |
16 |
5 |
0 |
19 |
32 |
36 |
|
|
|
||||||||||||||||||||||||
|
-вектор
столбец, состоящий из элементов
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
-
где
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3.2. Вычислить следующие суммы, пользуюсь таблицей 6.

3.3. Вычислить точечные оценки среднего, дисперсии, коэффициента корреляции.

3.4.
Вычислить 90% доверительный интервал
для коэффициента корреляции

3.4.1.
По таблице П5 по известному значению
найти Z
(если
 ).
).
3.4.2.
По таблице П1 найти квантиль нормального
распределения
 ( по условию дан 90% доверительный
интервал,
( по условию дан 90% доверительный
интервал,

3.4.3.
Вычислить доверительный интервал для
 по
формуле (1)
по
формуле (1)
 ;
;

3.4.4.
По таблице П5 по известным значениям
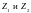 найти доверительный интервал для
найти доверительный интервал для

4. Контрольные вопросы.
Как составляется корреляционная таблица выборки двумерного случайного вектора?
Какие оценки числовых характеристик случайного вектора используются наиболее часто? Что они характеризуют?
Как вычисляются интервальные оценки вектора ?










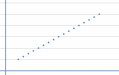
















 вектор строка, состоящая из элементов
вектор строка, состоящая из элементов
