Лабораторная работа №3. Проверка гипотезы о нормальном законе распределения по критерию согласия Пирсона.

Цель работы – проверка согласованности гипотезы о виде функции распределения выборки.

1. Краткие теоретические сведения. Статистические гипотезы можно разделить на гипотезы о законах распределения компонент случайной выборки и на гипотезы о параметрах распределения, т.е. о значениях параметров от которых зависит . Критерии, на основании которых делается вывод о согласованности гипотезы с данными, называются критериями согласия. Задача проверки гипотезы о том, что наблюдаемая случайная величина имеет заданную функцию распределения заключается в следующем. Согласно определению, должна быть близка к , при достаточно большом объёме выборки n. Выбирается некоторая неотрицательная мера K расхождения с и задаётся уровень значимости . С помощью известного распределения по заданному значению находится критическая точка из условия . По фактически заданной выборке , которая сравнивается с . Если при этом окажется, что , то это означает, что произошло событие, вероятность появления которого мала. В этом случае следует считать, что опытнее данные отвергать гипотезу. Если же , следует считать, что опытные данные согласуются с проверяемым предположением. Распределением с K степенями свободы называется распределение случайной величины 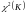, равное сумме квадратов K независимых нормально распределённых по закону случайных величин . Квантили распределения приведены в таблице П3. Распределение часто используется в статистических вычислениях в связи со следующей теоремой.

Теорема 2. Пусть элементы выборки независимы и распределены нормально с параметрами . Тогда и независимы, причём имеет распределение , а случайная величина имеет распределение . Проверка гипотезы о нормальном законе распределения. Пусть - выборка наблюдений случайной величины Х. Проверяется гипотеза , утверждающая, что Х имеет нормальный закон распределения, если уровень значимости равен . Процедура применения критерия для проверки гипотезы состоит в следующем:

1. Выбирается величина, являющаяся мерой расхождения статистического и теоретического законов распределения. За такую меру принимается величина .

2. Выборочное значение этой величины вычисляется по формуле , где ордината плотности нормального распределения.

3. Теоретическое значение определяется по таблице П3; l – число параметров распределения , которые оцениваются по выборке, r – число интервалов, на которые разбита выборка.

4. Гипотеза не противоречит выборке наблюдений на заданном уровне значимости , если гипотеза отклоняется, если это условие не выполняется. Критерий использует тот факт, что случайная величина имеет распределение близкое к нормальному. Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось условие . Если в некоторых интервалах это условие не выполняется, то их следует объединить с соседним.

2. Задание. Проверить гипотезу о нормальном распределении выборки, применяя критерий . Принять уровень значимости

3. Прядок выполнения работы.

3.1. Составьте и заполните таблицу 5.

3.1.1 При вычислении 5-го столбца ординаты плотности нормального распределения взять из таблицы П2.

3.1.2. Для заполнения 6-го столбца проверить выполнение условия .Если в некоторых интервалах это условие не выполняется , то объединить их с соседними.

Таблица 5.

2,5 7,5 12,5 17,5 22,5 27,5	3 7 18 22 8 2	2,23 1,34 0,45 0,45 1,34 2,23	0,03 0,16 0,36 0,36 013 0,03	1,80 8,64 19,40 19,40 8,64 1,80	10,44 19,40 19,40 10,44	-0,44 -1,40 2,60 -0,44	0,02 0,10 0,35 0,02 =0,49

3. 1. 3. Вычислить , суммируя элементы последнего столбца.

3. 1. 4. Определить число степеней свободы распределения . По выборке оценивается 2 параметра и , поэтому l=2. Выборка разбита на 6 интервалов, поэтому r=6. Однако элементы 1-ой и 2-ой строчек, а также элементы 5-ой и 6-ой строчек столбца объединены, поэтому r=4

3. 1. 5. Найти по таблице П3. По условию: =0,1; r=4; l=2; r-l-1=1; =2,71.

3. 1. 6. Проверить выполнение условия . По полученным результатам принять статистическое решение.

4. Контрольные вопросы.

4. 1. Записать и изобразить графически функцию и плотности нормального распределения случайной величины.

   2. Изобразить графически -квадрат распределение случайной величины. Как определяется число степеней свободы этого распределения?

   3. В чём состоит процедура гипотезы о виде функции распределения с помощью критерия согласия ?