14.Удлинение - укорочение стержня при растяжении-сжатии. Закон Гука
Растяжение-сжатие—
вид продольной деформации стержня или
бруса, возникающий в том случае, если
нагрузка к нему прикладывается по его
продольной оси (равнодействующая сил,
воздействующих на него, нормальна
поперечному сечению стержня и проходит
через его центр масс).Вызывается как
силами, приложенными к концам стержня,
так и силами, распределёнными по объёму
(силы инерции и тяготения).Растяжение
вызывает удлинение стержня (также
возможен разрыв и остаточная деформация),
сжатие вызывает укорочение стержня
(возможна потеря устойчивости и
возникновение продольного изгиба).В
поперечных сечениях бруса возникает
один внутренний силовой фактор —
нормальная сила.
l
- первоначальная длина стержня; Δl
– абсолютное удлинение(абсолютное
укорочение); ℰ=
Δl/l
– относительное удлинение(относительное
укорочение)При упругой деформации
зависимость между напряжением и
относительной деформацией определяется
законом Гука.
,
где Е
– модуль продольной упру гости, некоторая
физическая постоянная, которая
характеризирует материал.
15.Коэффициент Пуассона
Коэффициент Пуассона – отношение деформации по незагруженному направлению к деформации по загруженному направлению. Характеризует упругие свойства материала. Коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемого тела при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5
,
где μ — коэффициент Пуассона;
=
Δa/a
— деформация в поперечном направлении
(отрицательна при осевом растяжении,
положительна при осевом сжатии);ε —
продольная деформация (положительна
при осевом растяжении, отрицательна
при осевом сжатии).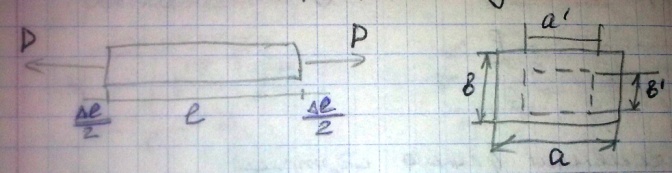
Δl – абсолютная продольная деформация(удлинение)
Δa=a-a ́ – абсолютная поперечная деформация
16. Допускаемое напряжение
Опасность
наступления разрушения характеризуется
не столько величинами внутренних усилий
в сечении, сколько величинами наибольших
нормальных напряжений, которое действует
в опасных (т.е. наиболее напряженных)
точках сечения, поэтому величины
наибольших нормальных напряжений
необходимо ограничить некоторыми
допустимыми величинами. Эти допустимые
значения называются допускаемыми
напряжениями. [
]
– допускаемое напряжение; [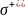
]
– на растяжении; [
]
– на сжатии.
17. Условие прочности бруса при растяжении - сжатии. Три типа разрешимых задач.
При
растяжении-сжатии стержня находят
сечение, в которых напряжение достигает
наиб. Значение и записывают условие
прочности, т.е.
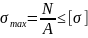
При растяжении в правую часть этого неравенства, подставляют [ ], при сжатии - [ ]
[
]=
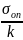
Допускаемая
величина напряжения расчетная:
,
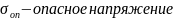для пластичных материалов
(предел
текучести), для хрупких -
(прочности)
Решают 3 типа задач:
Проектирующий расчет
Дано:
Р, [
].
По известным нагрузкам для выбранного
материала находят с точки зрения
прочности размеры поперечного сечения,
т.е. проектируют какой-то элемент.
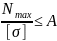
P
– нагрузка,
-
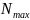продольная сила.
Проверочный расчет
Дано: Р, А. По известным размерам и материалам деталей проверяем, может ли она выдержать заданную нагрузку.
Определение допускаемой нагрузки
Дано:
,
А. По известным размерам деталей,
материалы и схеме загружения определяем
допустимую величину нагрузки: [p]=
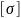*A