Критерий Гурвица

Матрица Гурвица:

.

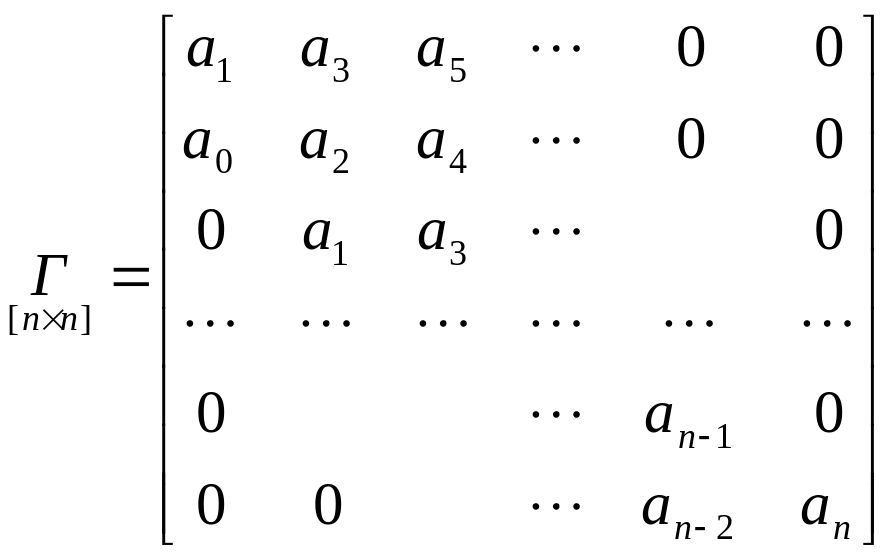На главной диагонали в порядке возрастания располагаются коэффициенты . Каждый из столбцов заполняется вверх с возрастающими индексами, вниз – с убывающими индексами.

Определение устойчивости по Гурвицу: для устойчивости линейной системы необходимо и достаточно чтобы были положительны главных определителей матрицы Гурвица.

Главные определители имеют вид:

;

;

;

.

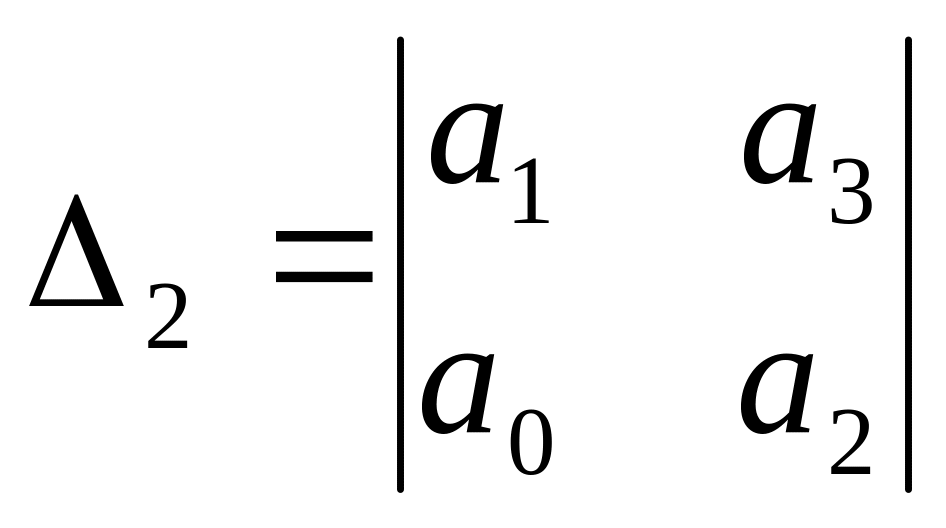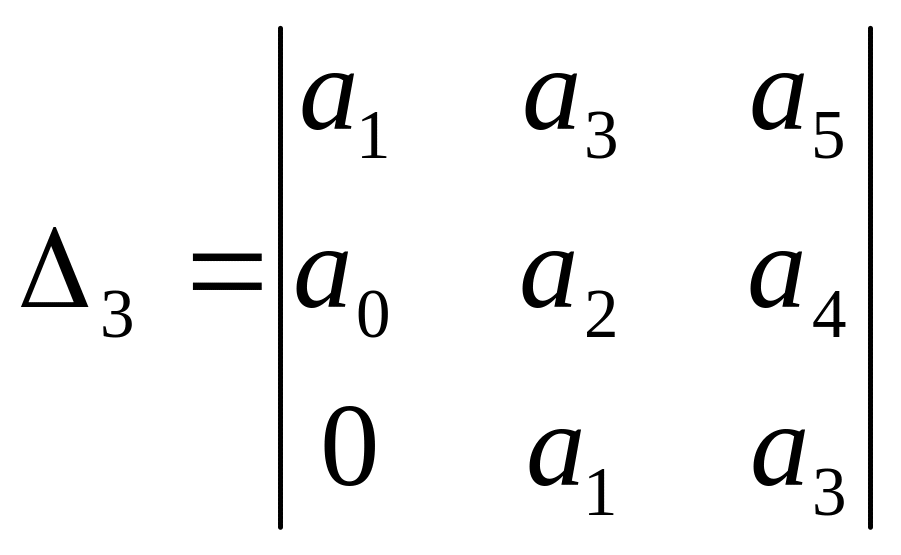Гурвиц показал, что:

• если 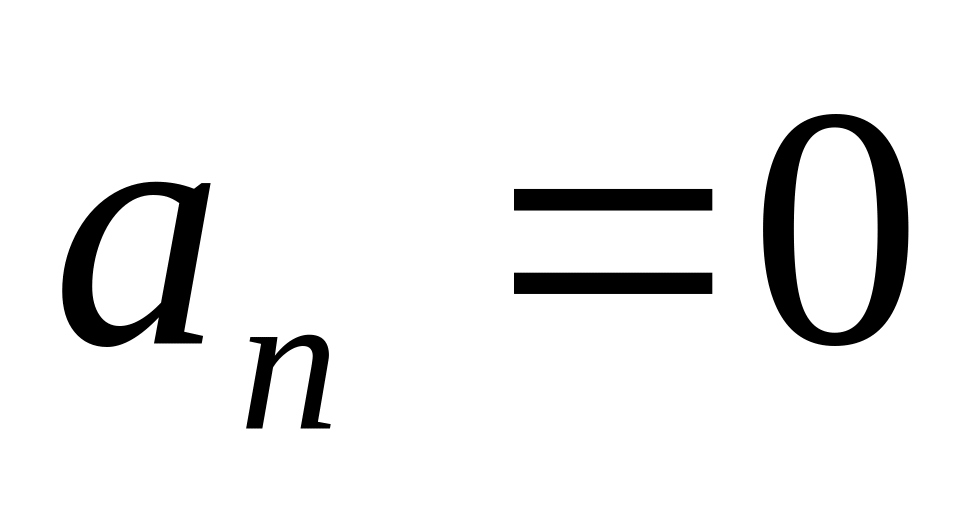, то система находится на границе апериодической устойчивости;

• если 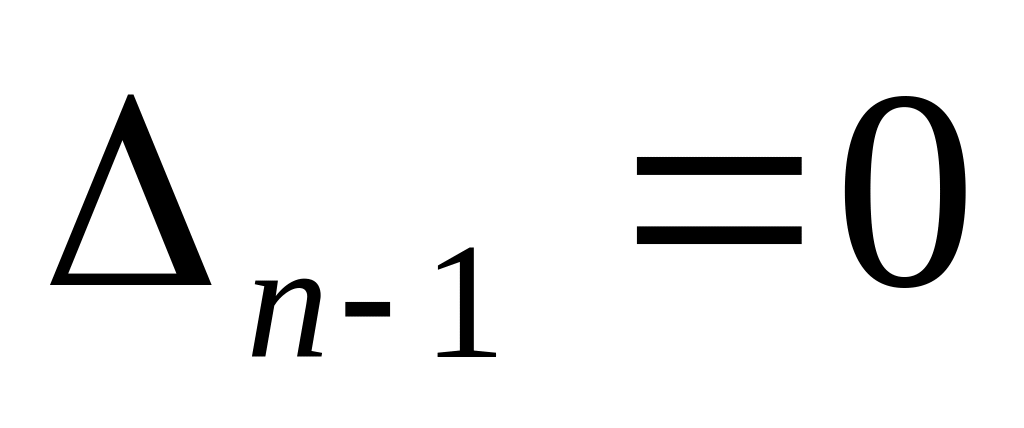, то система находится на границе колебательной устойчивости, т.е. есть пара мнимых корней.

Пример

Задано характеристическое уравнение:

Определить значения параметров , и при которых система устойчива.

Решение:

;

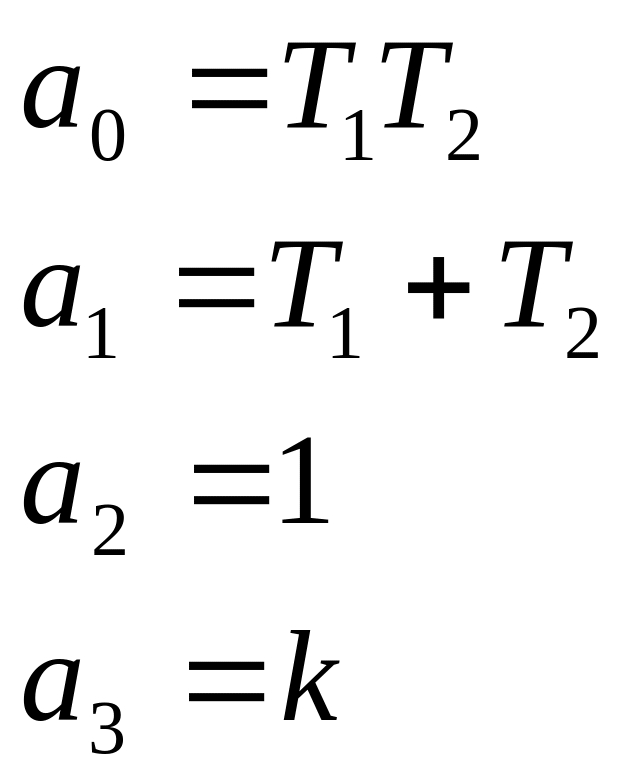
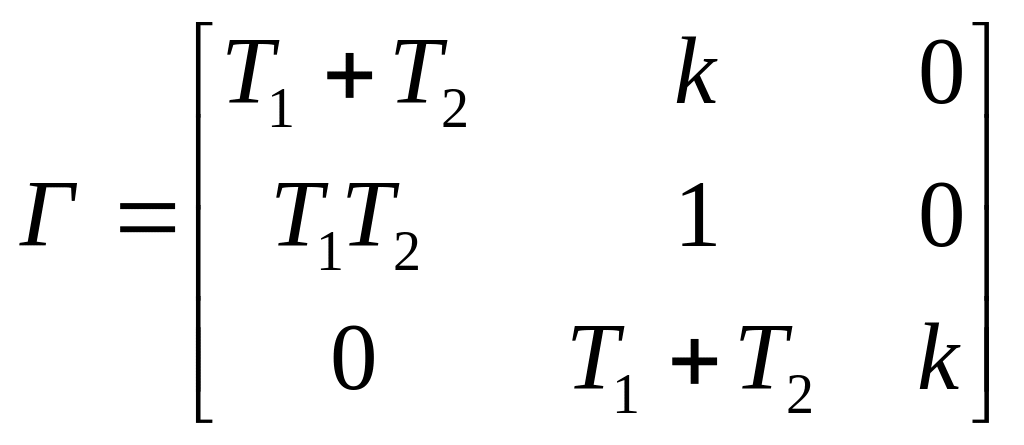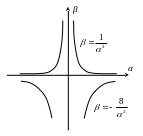
Область устойчивости для параметра :

– нижняя граница;

– верхняя граница.

Пример

Задана матрица :

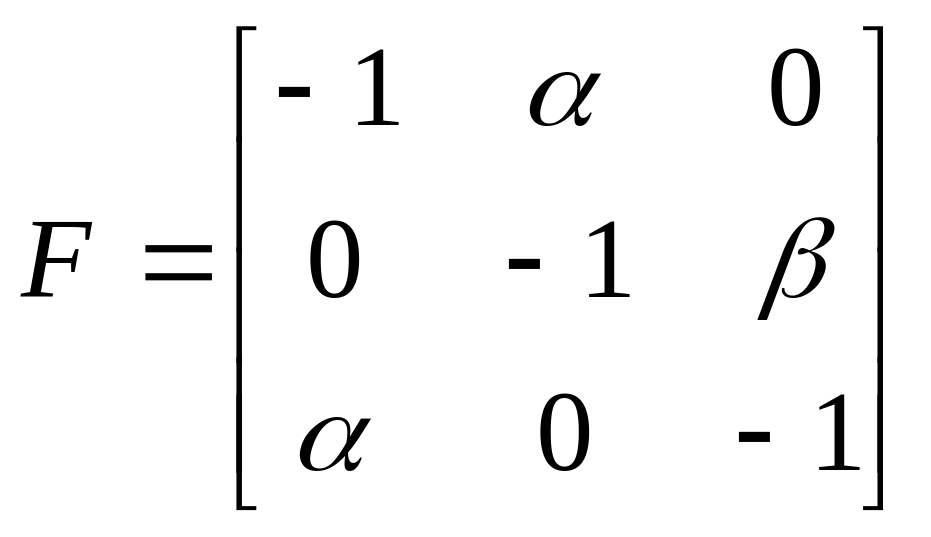
Определить устойчивость.

Решение:

;

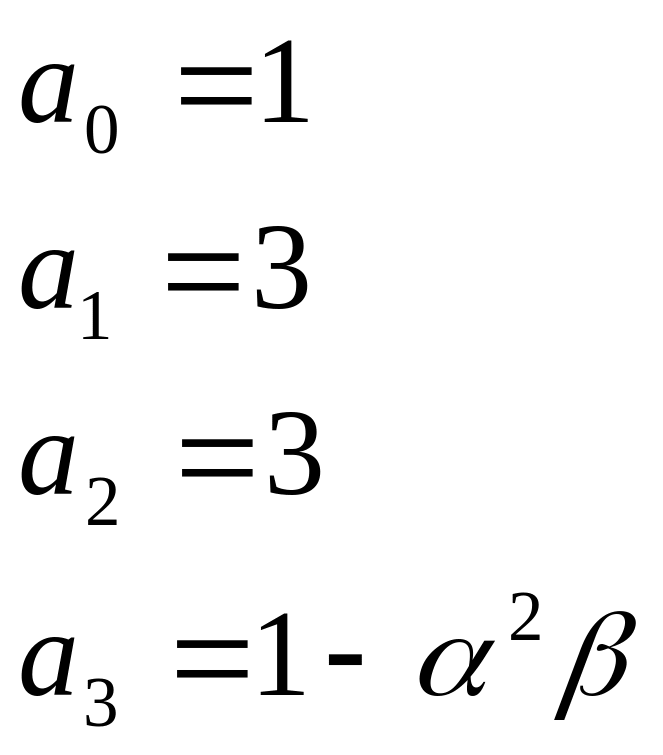
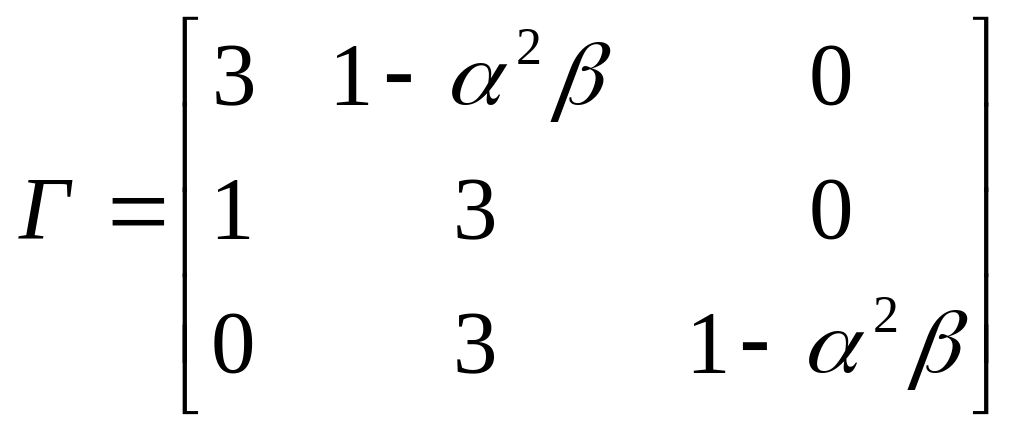
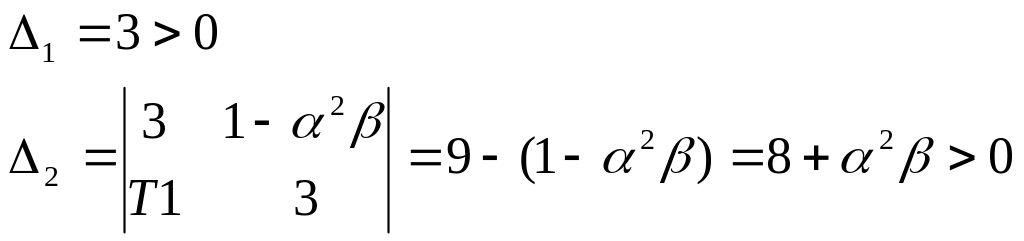
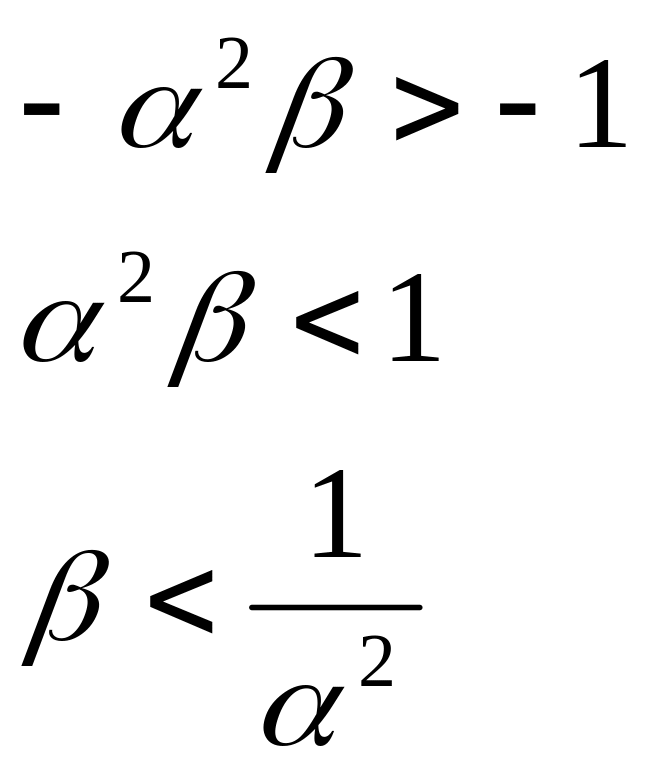
Область устойчивости:

Критерий Михайлова

Основой для критерия является комплексная частотная характеристика.

;

– связано с устойчивостью (т.к. это характеристический многочлен).

Для построения годографа меняют значения от 0 до .

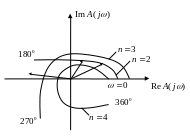
Для устойчивости линейной системы по отклонению начальных условий с частотной характеристикой необходимо и достаточно, чтобы годограф характеристического многочлена при изменении частоты от 0 до , охватывал начало координат на угол

, где

– угол;

– порядок характеристического многочлена.

Алгоритм:

1. Определить порядок знаменателя комплексно-частотной характеристики ;

2. Построить на комплексной плоскости годограф , ;

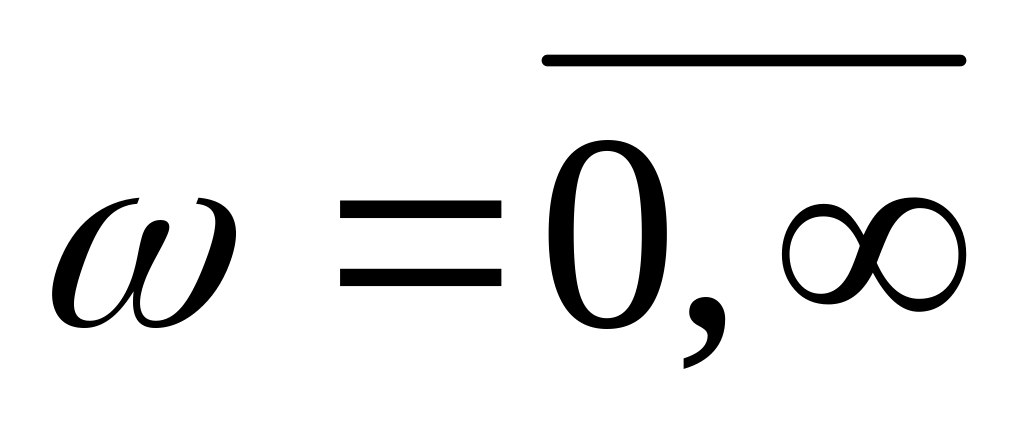3. Рассчитать величину угла на которой годограф охватывает начало координат , ;

4. Проверить выполнение условий. Если приращение равно 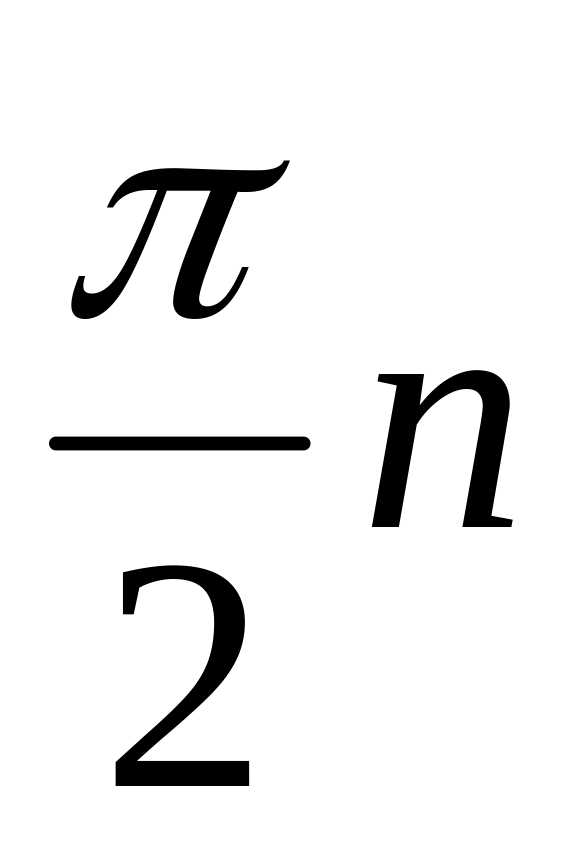, то система устойчива.

Пример

;

;

;

.

0
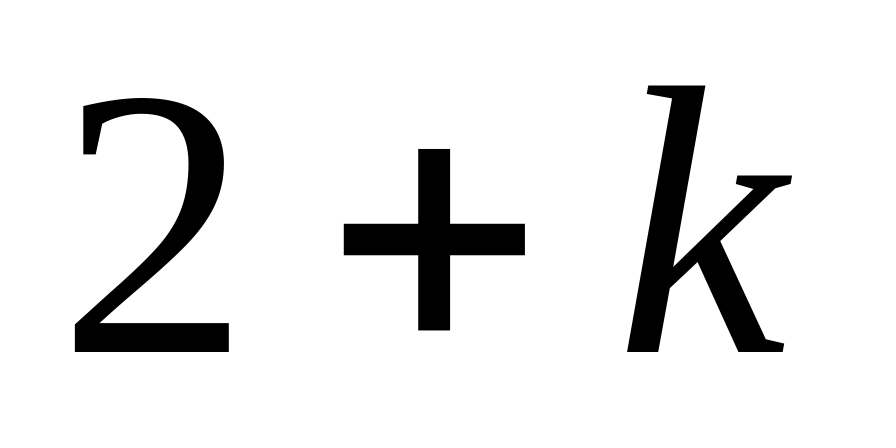
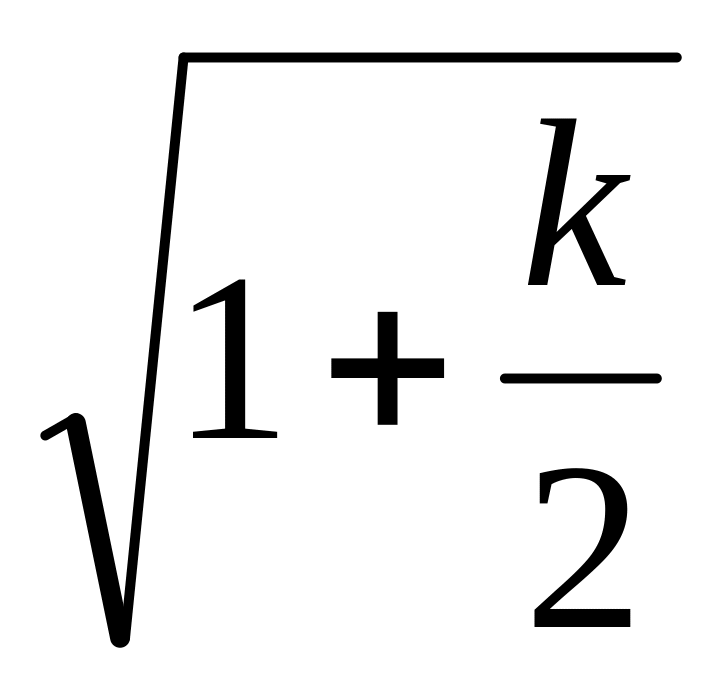
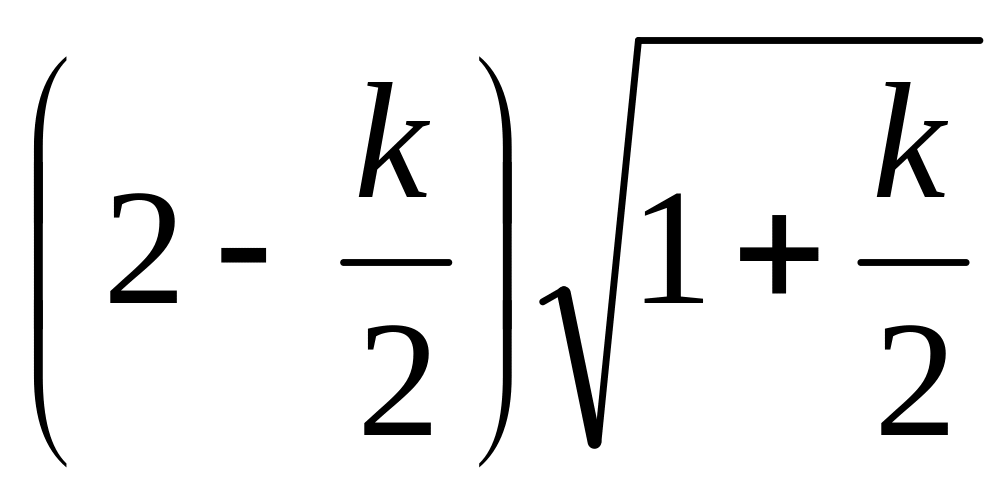
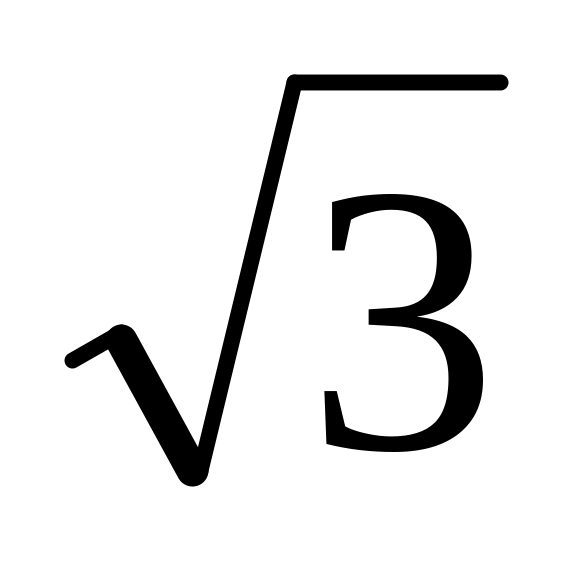
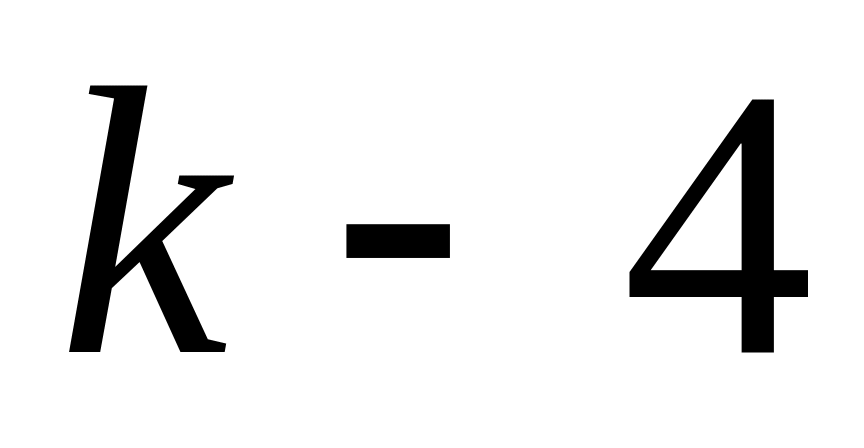
3

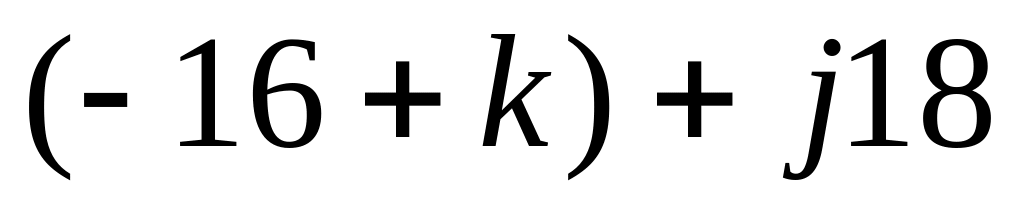
Управляемость сау

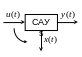
Если на интервале выбрать , и управление ограничено 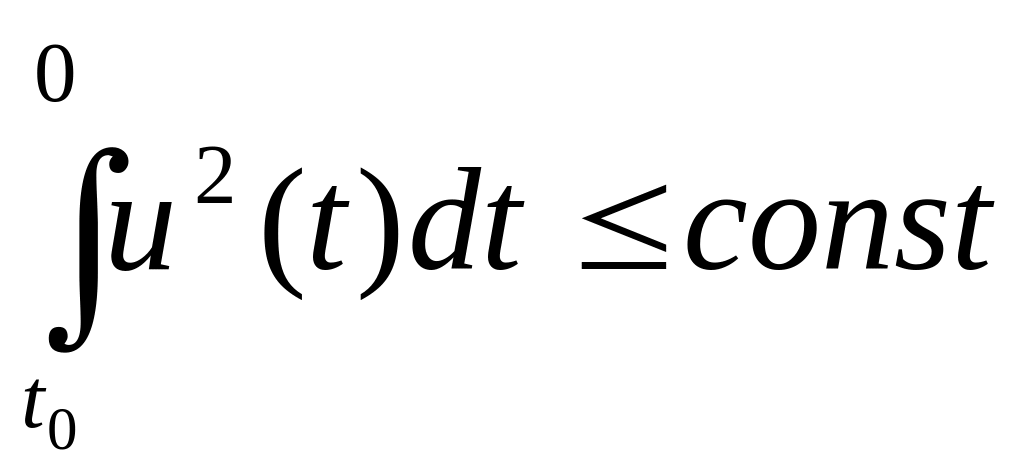, то говорим, что система управляема.

Основной задачей ТАУ является разработка методов проектирования управляющих устройств (регуляторов), обеспечивающих требуемое качество управления.

Рассмотрим свойства САУ: управляемость и наблюдаемость.

Управление объектом требует создание такой управляющей функции , при которой входные переменные и компоненты вектора состояния воспроизводят некоторые заданные (желаемые) функции времени.

Возникает вопрос об условиях, выполнение которых гарантирует реализацию такого управления, а также возможность наблюдения результатов такого управления.

Можно ли в рамках допустимых управляющих воздействий достичь цели управления? Эти вопросы приводят к понятию управляемости системы.

Система называется полностью управляемой, если для любой точки пространства состояний существует некоторое ограниченное управление , позволяющее перевести систему за конечное время из произвольного начального состояния в произвольное конечное состояние этого пространства.

Теорема Калмана

Для линейных стационарных систем, описанных дифференциальными уравнениями:

необходимым и достаточным условием является следующая характеристика системы:

– матрица управляемости, ранг которой должен быть равен порядку системы:

.

Если , то система не полностью управляема, при этом можно выделить управляемую часть системы порядка , остальная часть будет не управляемой.

Пример

Определить, является ли система управляемой.

Решение:

; ;

; .

;

;

; ;

система не является управляемой.

Пример

Определить, является ли система управляемой.

Решение:

; ; .

;

;

система управляемая (невырожденная матрица).

Пример

Определить, является ли система управляемой.

Решение:

; .

; .

;

;

система управляемая.

Наблюдаемость САУ

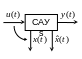
Для того чтобы управлять системой надо иметь информацию о ее состоянии. Обычно она содержится в измеряемых сигналах выхода, т.е. компонентах . Однако по измеряемым далеко не всегда приходится определять состояние системы. Задача наблюдаемости состоит в том, чтобы определить вектор состояния или его оценку по данным о входах системы и выходах системы .

Различают две задачи наблюдаемости системы:

1. Система наблюдаема на интервал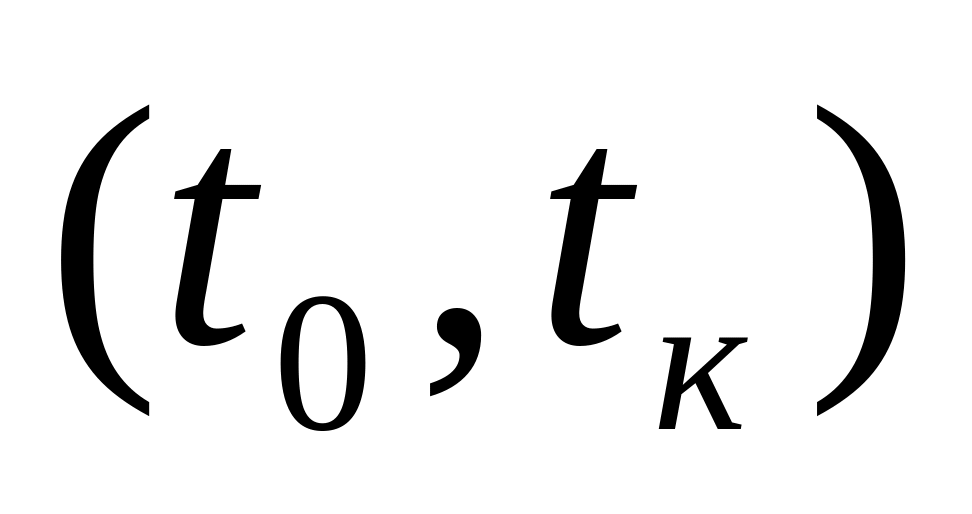е , где , если по известной паре 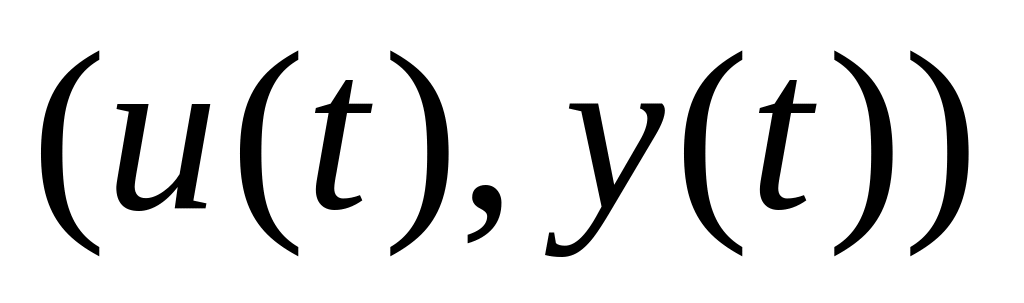можно определить состояние системы при условии что 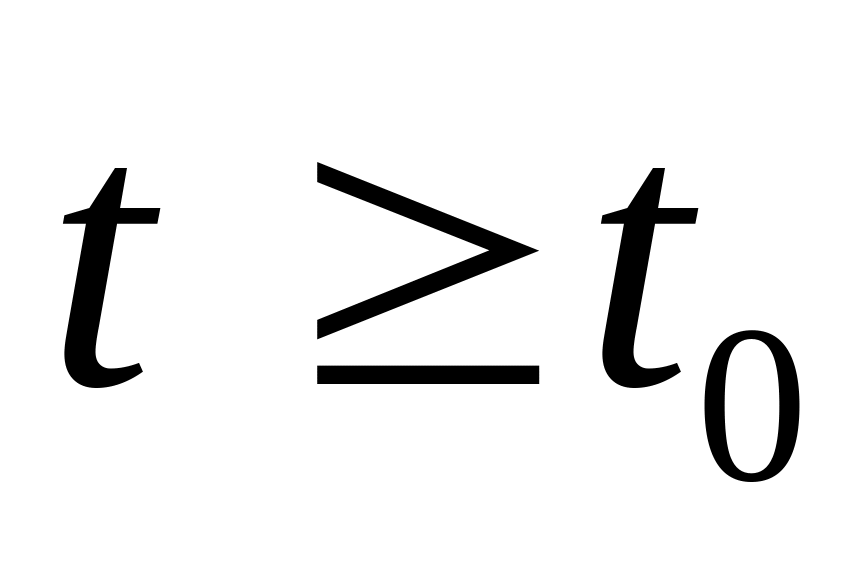. Эта задача называется задачей восстановления.

2. Если есть пара , то есть возможность оценить состояние системы 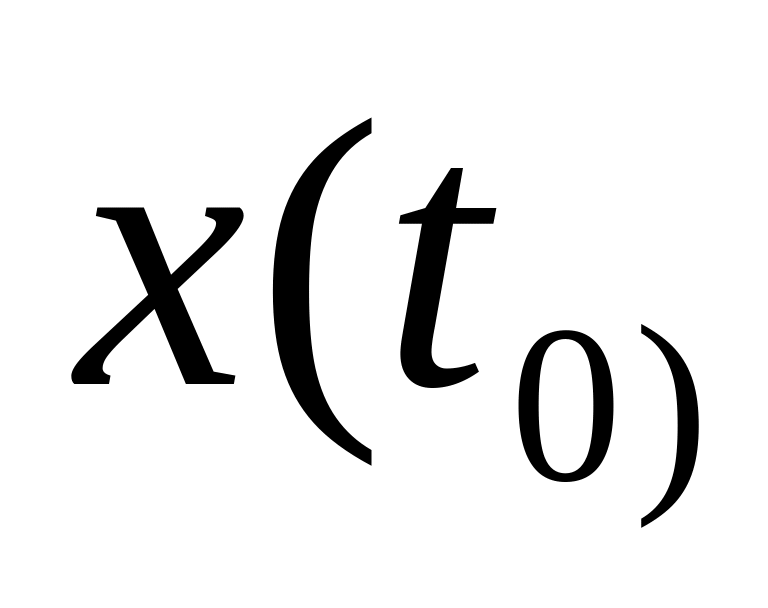в момент времени 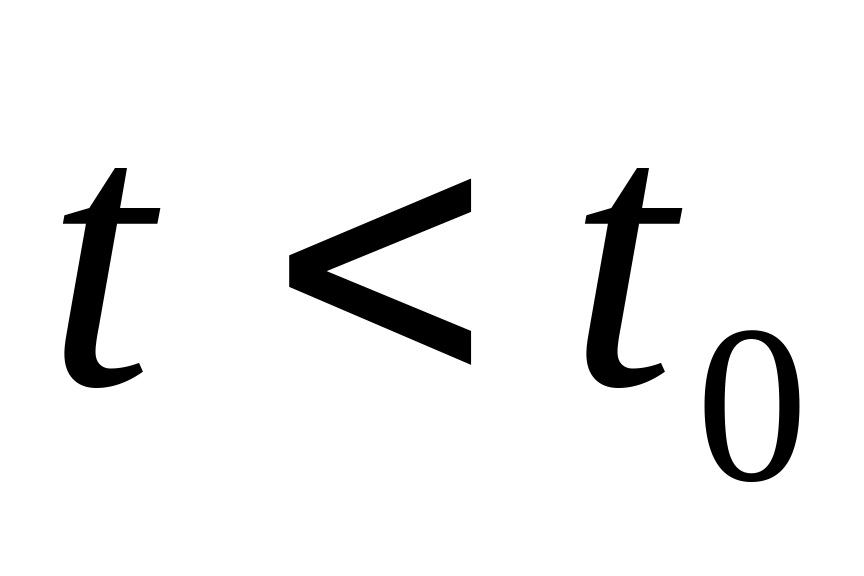. Это задача идентификации.

Система называется полностью наблюдаемой в интервале , если коэффициенты вектора состояний могут быть определены на основании наблюдений (измерений) пары .