Определение устойчивости по Ляпунову

Невозмущенное движение называется устойчивым по отношению к отклонениям начальных условий , если при всяком произвольно заданном положительном , как бы мало оно не было, можно выбрать другое положительное число , что при всяком возмущении в 0 удовлетворяет условию:

и при любом будет выполнятся неравенство:

. – норма вектора отклонения в -мерном пространстве.

В противном случае движение системы не устойчивое.

Несколько интерпретаций теоремы Ляпунова

1. Если невозмущенное движение устойчиво, то при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения;

2. Если невозмущенное движение не устойчиво, то возмущенное движение будет отходить от него, как бы малы не были начальные возмущения;

3. Если невозмущенное движение устойчиво и при этом любое возмущенное движение при малых начальных возмущениях стремиться к невозмущенному движению, при этом норма вектора будет стремиться к 0, то невозмущенное движение называется асимптотически устойчивым

.

Линейная стационарная система асимптотически устойчива тогда и только тогда, если корни характеристического уравнения имеют отрицательные вещественные части.

Пусть , тогда возмущенным движением будет реальная траектория системы.

- возмущение.

;

;

;

; – определяется корнями характеристического уравнения

– определяется только матрицей динамики

– корни характеристического уравнения.

;

,

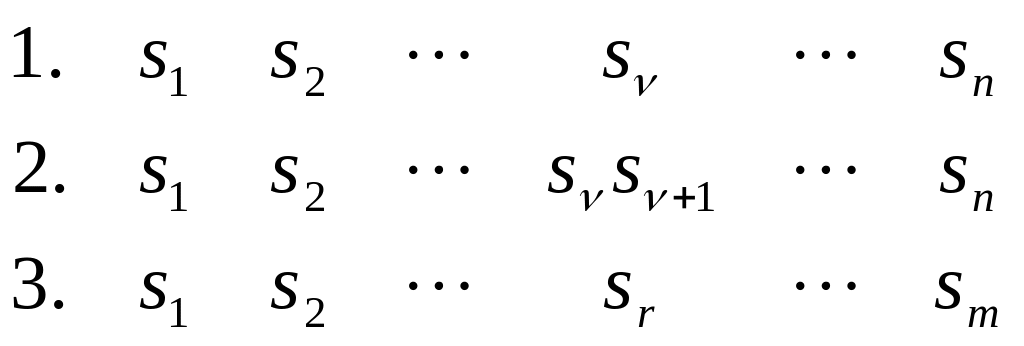– кратный корень -ой кратности.

1. Пусть корни характеристического уравнения простые и вещественные 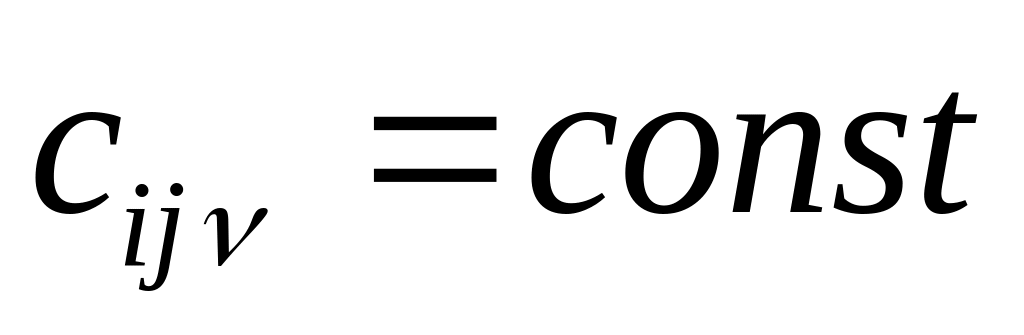Если корни , то

2. ,

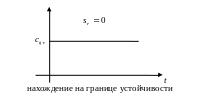
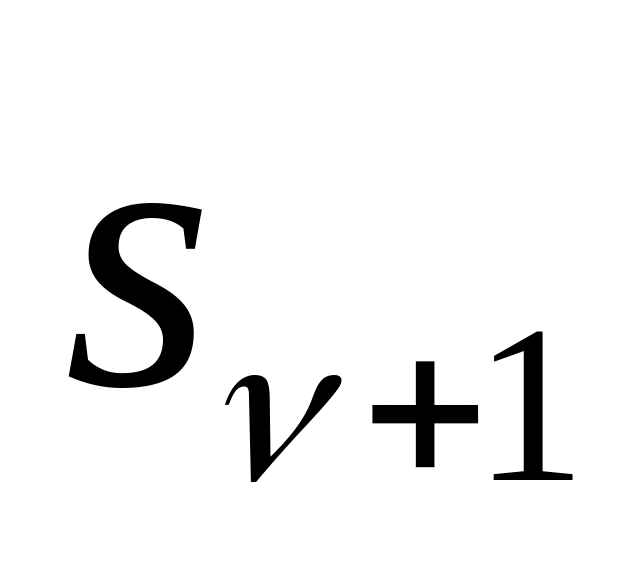
 – устойчивая система второго порядка (вещественная часть отрицательная);

 – неустойчивая система третьего порядка;

 – апериодическая устойчивость;

 – колебательная устойчивость;

– запас устойчивости для устойчивой системы.

Теорема

Линейная система является устойчивой по Ляпунову, если все характеристические числа динамики матрицы имеют отрицательные или нулевые вещественные части, причем в последнем случае характеристические числа должны быть простые. При нарушении хотя бы одного из условий система не устойчива.

Линейная система асимптотически устойчива тогда и только тогда, когда все характеристические числа матрицы имеют отрицательные вещественные части.

Примечание: если в характеристическом уравнении имеется хотя бы один нулевой корень или хотя бы одна пара чисто мнимых корней , а все остальные корни имеют отрицательные вещественные части, то говорят, что система находится на границе устойчивости. В первом случае граница апериодической устойчивости, во втором – граница колебательной устойчивости.

– асимптотически устойчивая система

.

Критерии устойчивости

Для определения устойчивости систем высокого порядка выделяют правила, которые позволяют определить устойчивость системы без вычисления корней характеристического уравнения. Эти правила называются критериями устойчивости. Они бывают:

• Алгебраические:

• критерий Рауса;

• критерий Гурвица;

• критерий Льенара

• Частотные:

• критерий Михайлова;

• критерий Найквиста.