
- •Лекции по теории автоматического управления Оглавление
- •Принцип действия сау и классификация сау
- •Классификация сау
- •Примеры сау Генератор постоянного тока
- •Робототехнический комплекс
- •Математические модели объектов и сау
- •Математическая модель сау в терминах преобразования «вход/выход»
- •Передаточная функция системы
- •Преобразования Лапласа
- •Весовая функция системы
- •Переходная функция системы
- •Описание структуры сау
- •Комплексная частотная характеристика сау
- •Усилительное звено
- •Интегрирующее звено
- •Апериодическое звено
- •Пример (последовательное соединение звеньев)
- •Пример (параллельное соединение)
- •Преобразования используемые для описания системы в пространстве состояний Процедура 1
- •Методы расчета фундаментальной матрицы
- •Пример (вычисление фундаментальной матрицы)
- •Продолжение
- •Анализ сау
- •Алгоритм решения задачи анализа
- •Свойства сау
- •Устойчивость сау
- •Определение устойчивости по Ляпунову
- •Несколько интерпретаций теоремы Ляпунова
- •Теорема
- •Критерии устойчивости
- •Критерий Гурвица
- •Критерий Михайлова
- •Управляемость сау
- •Теорема Калмана для оценки наблюдаемости
- •Синтез сау
- •Синтез сау с помощью отрицательной обратной связи для стабилизации системы.
- •Теорема
- •Алгоритм построения регулятора
- •Стабилизация системы с помощью отрицательной обратной связи в условиях неполной информации
- •Наблюдатель линейной системы Теорема
- •Стабилизирующая обратная связь по наблюдениям выходного сигнала (при включении наблюдателя в обратную связь)
- •Алгоритм построения регулятора и наблюдателя
- •Оптимальное управление сау
- •Классификация задач оптимального управления
- •Задача построения оптимального регулятора с помощью отрицательной обратной связи (методом Калмана)
- •Теорема Калмана в задачи оптимальной стабилизации
- •Алгоритм решения задачи по построению оптимальной отрицательной обратной связи
- •Принцип максимума Понтрягина
- •Теорема
- •Методы линейного программирования
- •Пример (продавец газет)
- •Пример:
- •Приложение Основные понятия линейной алгебры
- •Системы линейных уравнений: правило Крамера
Методы расчета фундаментальной матрицы
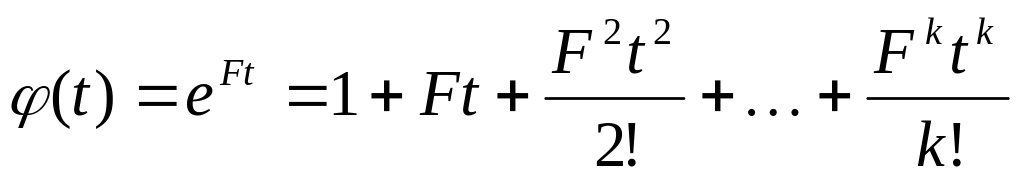 –
ряд Фурье
–
ряд ФурьеИспользование операторного метода
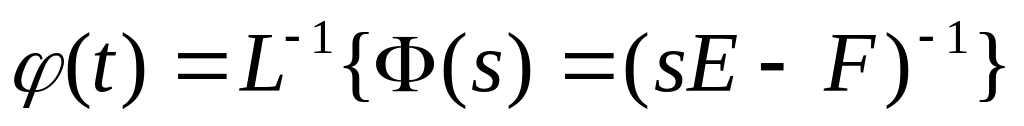 ;
;
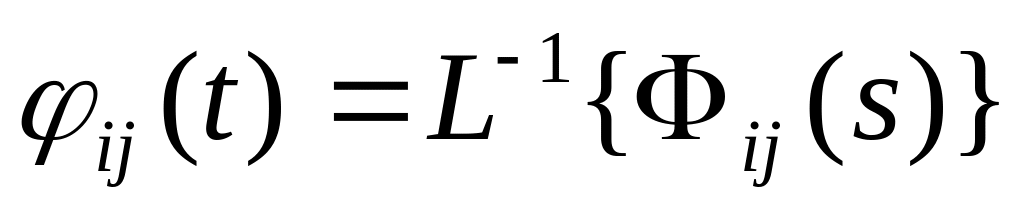 ;
; 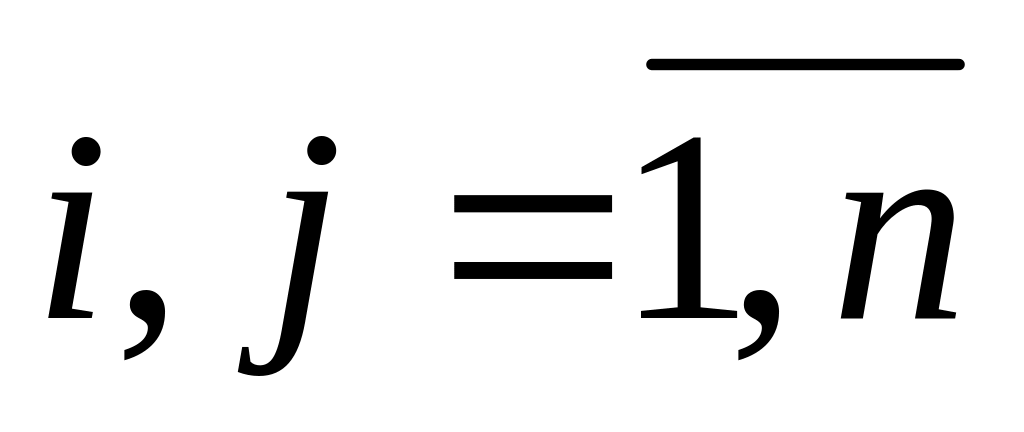 .
.
Пример (вычисление фундаментальной матрицы)
Пусть задана система в виде:
![]() ;
; ![]() – произвольные.
– произвольные.
Вычислить фундаментальную матрицу системы .
Решение:
![]() ;
;
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
![]()
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Продолжение
Элементы матрицы
![]() имеют вид, зависящий от корней
характеристического уравнения
.
имеют вид, зависящий от корней
характеристического уравнения
.
Если корни характеристического уравнения простые (некратные, вещественные), то элемент
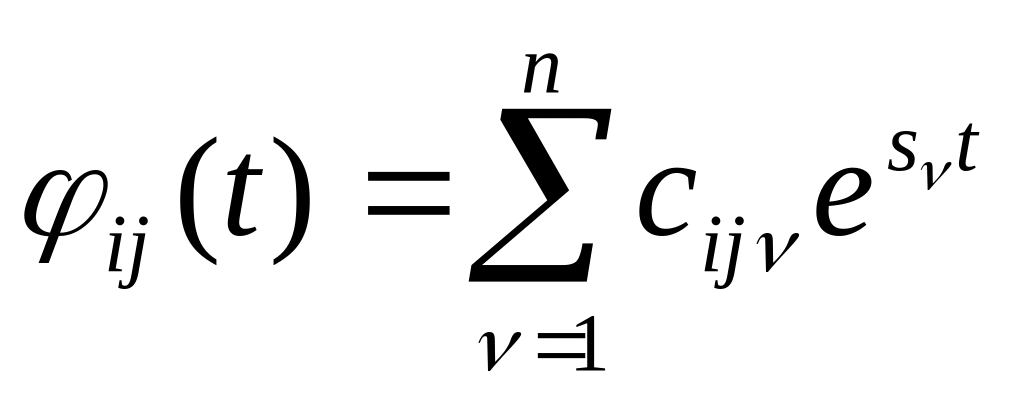 , где
, где
 – корни характеристического уравнения;
– корни характеристического уравнения;
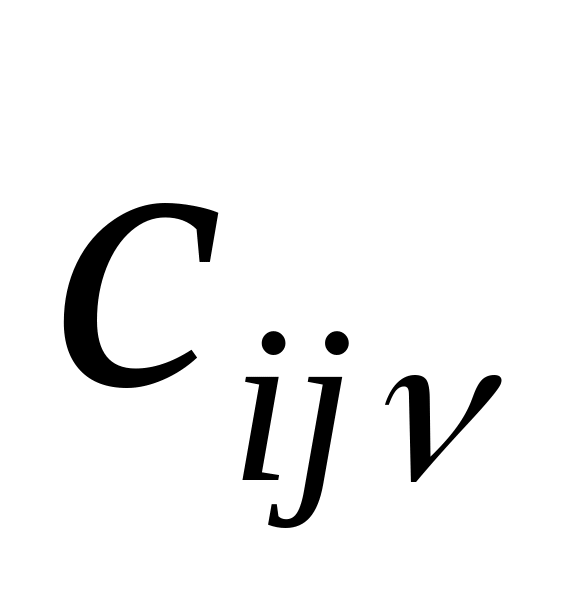 – числа, которые являются коэффициентами
разложения на простые дроби элементов
– числа, которые являются коэффициентами
разложения на простые дроби элементов
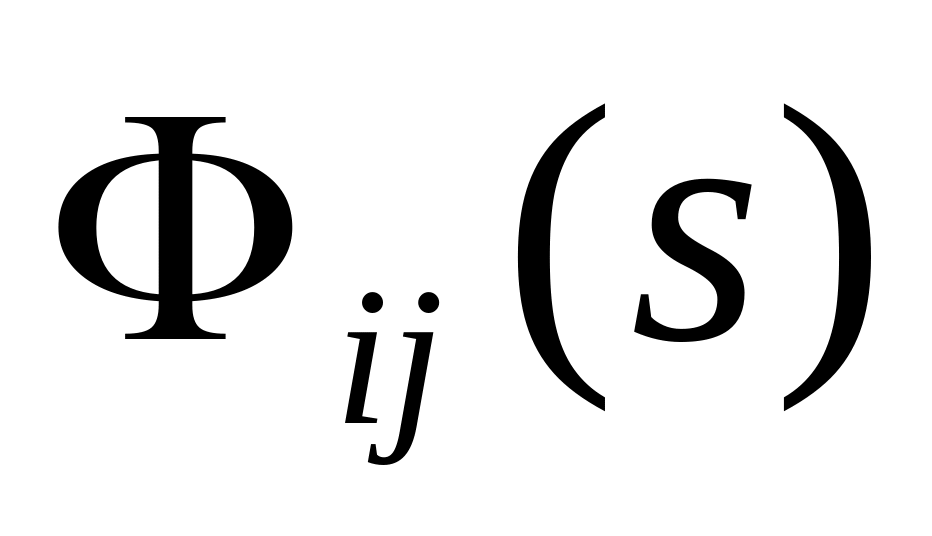 .
.
Если корни характеристического уравнения комплексно-сопряженные, то
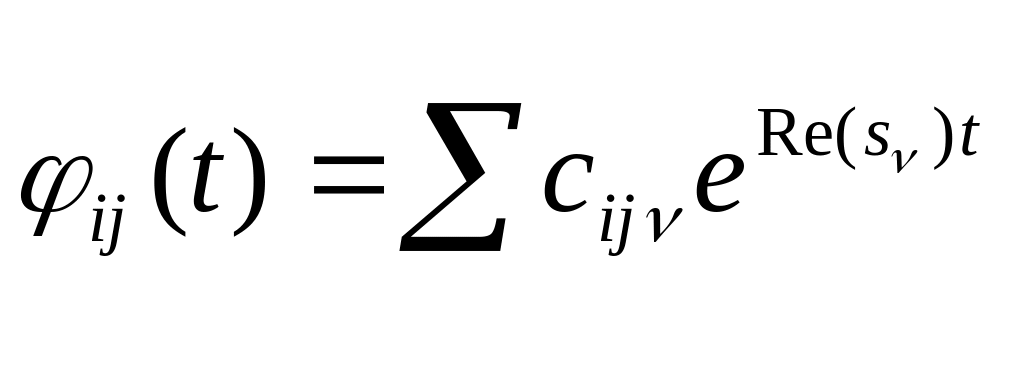 , где
– гармоническая составляющая
, где
– гармоническая составляющая
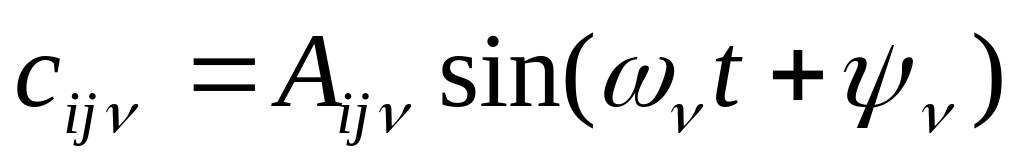 ;
;
 ;
;
 ;
;
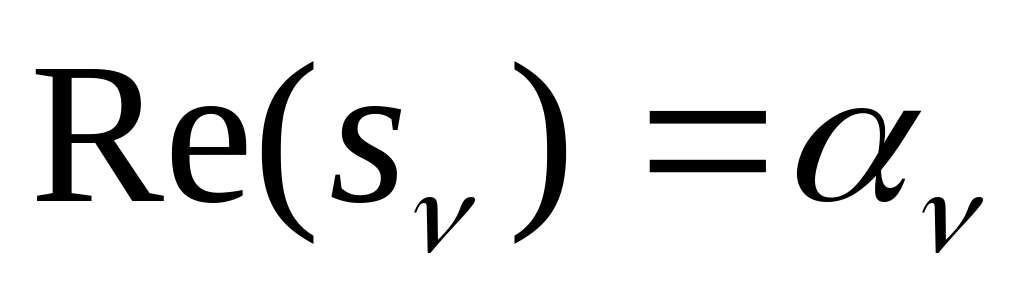 .
.

Если корни вещественные, кратные –
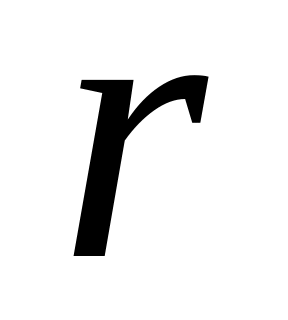 -ой
кратности
-ой
кратности
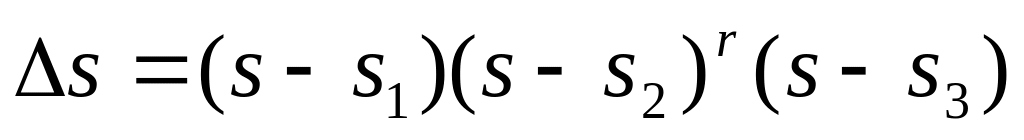 ;
;  ;
;
 .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
Представление
показывает, что матричная экспонента
является матрицей, каждая компонента
которой линейная комбинация скалярной
экспоненты
![]() ,
а т.к. весовые матицы
,
а т.к. весовые матицы
![]() и
и
![]() соответственно равны
и также имеют своими
компонентами линейные комбинации тех
экспонент. Вид этих экспонент (затухающие
или возрастающие) определяют траекторию
движения системы
и
.
соответственно равны
и также имеют своими
компонентами линейные комбинации тех
экспонент. Вид этих экспонент (затухающие
или возрастающие) определяют траекторию
движения системы
и
.
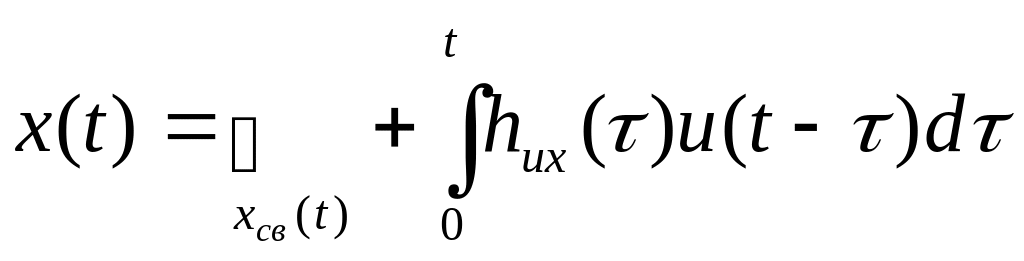 ;
;
;
![]() .
.
Анализ сау
Для анализа дано:
входные воздействия ;
линейная система, описываемая уравнением:
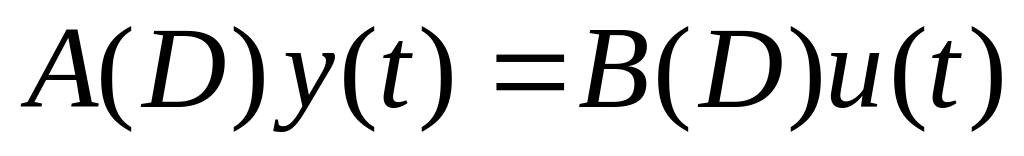 , где
, где
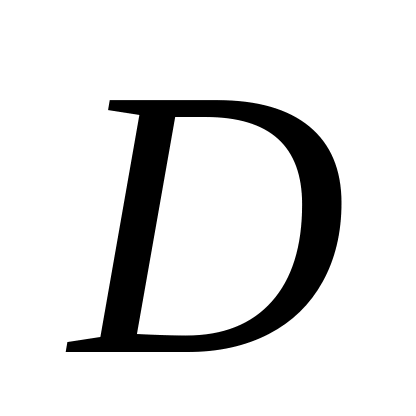 – оператор дифференцирования;
– оператор дифференцирования;начальные ненулевые условия в виде:

Найти выходной сигнал этой системы на заданное входное воздействие .
Алгоритм решения задачи анализа
![]() ;
;
![]() –
– ![]() ;
; ![]() ;
;
![]() –
;
–
; ![]() .
.
Найти изображение входных сигналов ;
Определить передаточную функцию системы
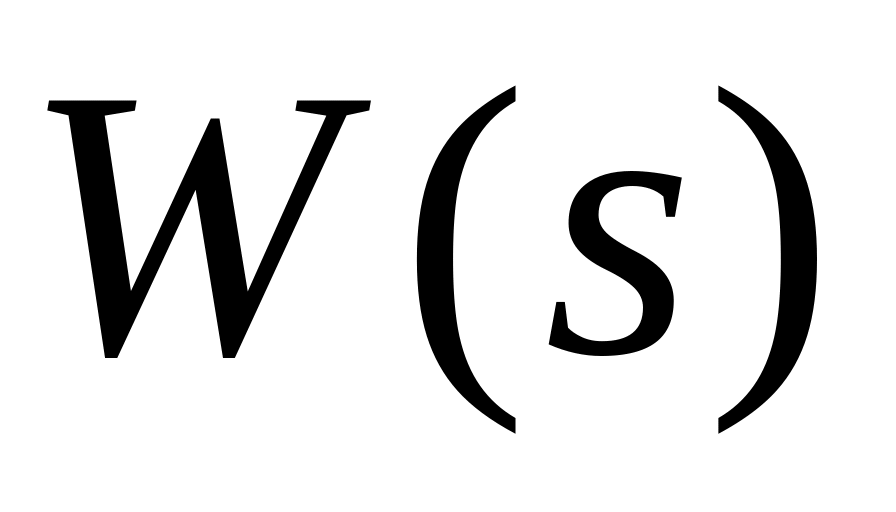 одним из методов преобразования
структурных схем и если начальные
условия ненулевые, то найти многочлены
одним из методов преобразования
структурных схем и если начальные
условия ненулевые, то найти многочлены
 и
и
 по следующим формулам:
по следующим формулам:

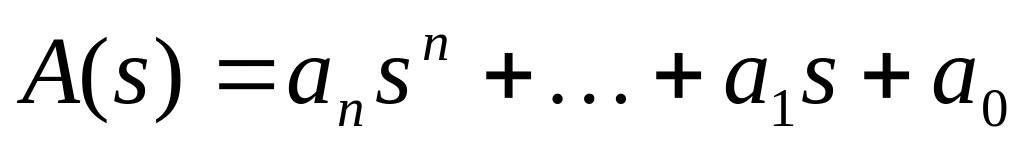
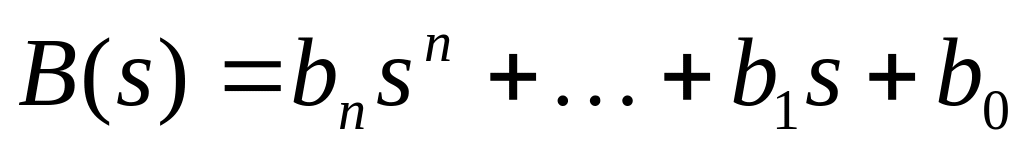
Найти изображение выходного сигнала
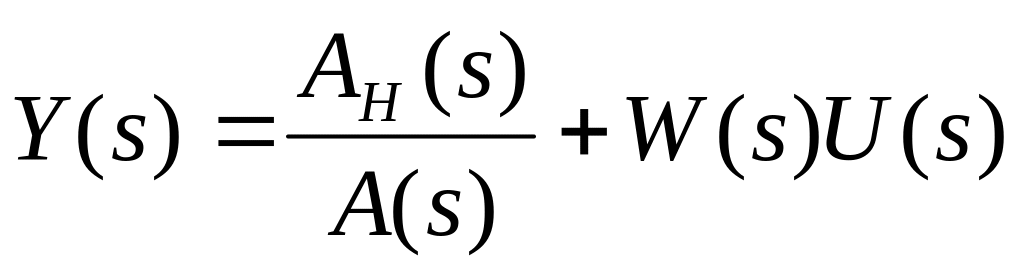 ;
;
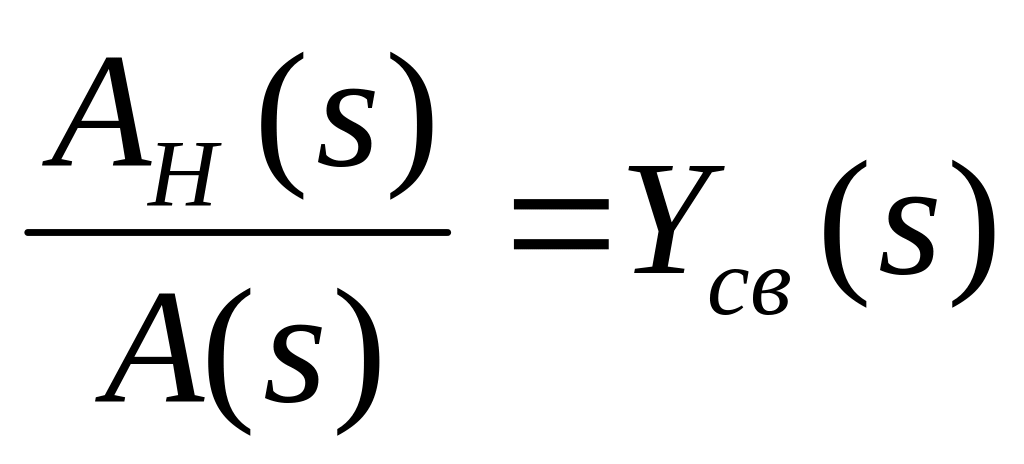 ;
;
;
;
 .
.Найти реакцию системы (выходной сигнал) .
Пример
Найти реакцию системы, описываемой дифференциальным уравнением
с начальными условиями
![]() ;
;
![]() ;
;
на входной сигнал
![]() .
.
Решение:
![]() ;
;
![]() ;
;
![]()
![]() .
.
Найдем корни :
;
![]() ;
;
![]() .
.
![]() ;
;
Используем процедуру 3.
![]() ;
;
![]() ,
при
,
при
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
Решим этот же пример используя процедуру 1.
![]() ;
;
![]() ;
;
![]() ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;

![]()
![]() .
.
Свойства сау
Анализ САУ требует определения процессов протекающих в САУ, свойств анализирующих в САУ, таких как:
устойчивость;
управляемость;
наблюдаемость.
Понятие устойчивости является фундаментальным понятием.
Устойчивость сау
Устойчивость САУ является одним из важнейших условий ее работоспособности, которое определяется требованиями затухания переходных процессов во времени.
Правильно спроектированная система должна правильно работать при всех внешних воздействиях.
Говоря об устойчивости САУ выделяют:
Устойчивость состояния равновесия системы – способность возвращаться в это состояние, после того, как исчезнет возмущение – причина отклонения;
Устойчивость заданного (траектории) движения – способность системы отвечать на малые начальные отклонения малым же отклонением реального движения от исходной траектории.
.
Пусть
![]() – заданное невозмущенное движение
(траектория).
– заданное невозмущенное движение
(траектория).
![]()
Возмущение может быть из-за:
– возмущение по входу;
 – возмущение по отклонению начальных
условий.
– возмущение по отклонению начальных
условий.
 ;
;
 ;
;
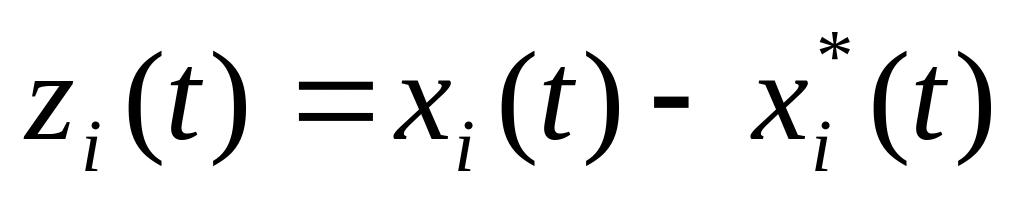 ;
– возмущенная траектория.
;
– возмущенная траектория.
Заданное невозмущенное движение
![]() будет устойчивым если после
приложения внешних сил (возмущений)
типа 1 и 2, которые потом снимают возмущенное
движение по истечении некоторого
времени, войдет в заданную область
будет устойчивым если после
приложения внешних сил (возмущений)
типа 1 и 2, которые потом снимают возмущенное
движение по истечении некоторого
времени, войдет в заданную область
![]() , где
, где
![]() – некоторая заданная величина,
определяющая область допустимых
значений.
– некоторая заданная величина,
определяющая область допустимых
значений.
В качестве невозмущенного движения может быть как свободная для исследования устойчивость, так и вынужденное движение.
