Преобразования используемые для описания системы в пространстве состояний Процедура 1
Для процедуры 1 взято дифференциальное уравнение -ого порядка:
Между переменными вектора состояний есть связь, они так выбраны, что:
(1
выход) 
(1
вход) порядок системы
; 
;
; 
.
Наиболее просто в пространстве состояний описывается система , если
и
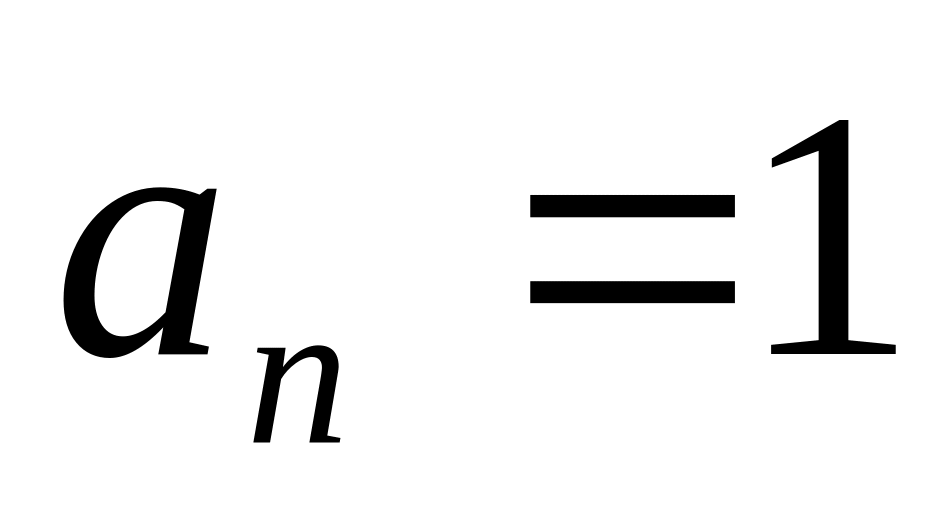.Если
,
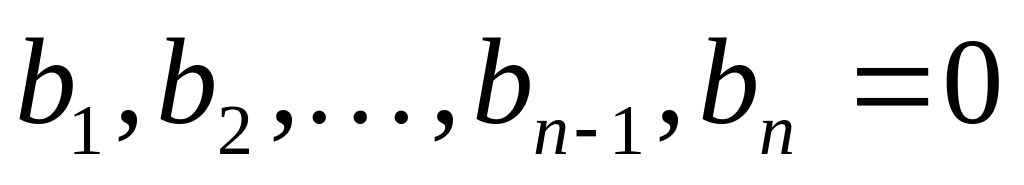а
,
то переменные состояния совпадают с
выходной переменной объекта и ее
производными.
Доказательство
, где
;
.
;
;
;
;
;
;
;
;
.
;
;
;
;
;
.
;
;
;
;
;
;
.
; ;
;
;
;
;
;
;
;
.
; .
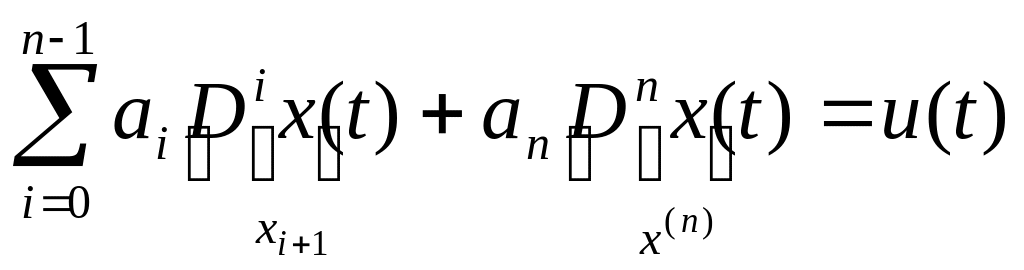Пример
Описать, используя процедуру 1, систему уравнений в пространстве состояний, если задано дифференциальное уравнение 2-ого порядка связывающее вход/выход в виде:
Решение:
; ; ;
; 
;
; 
;
; 
.
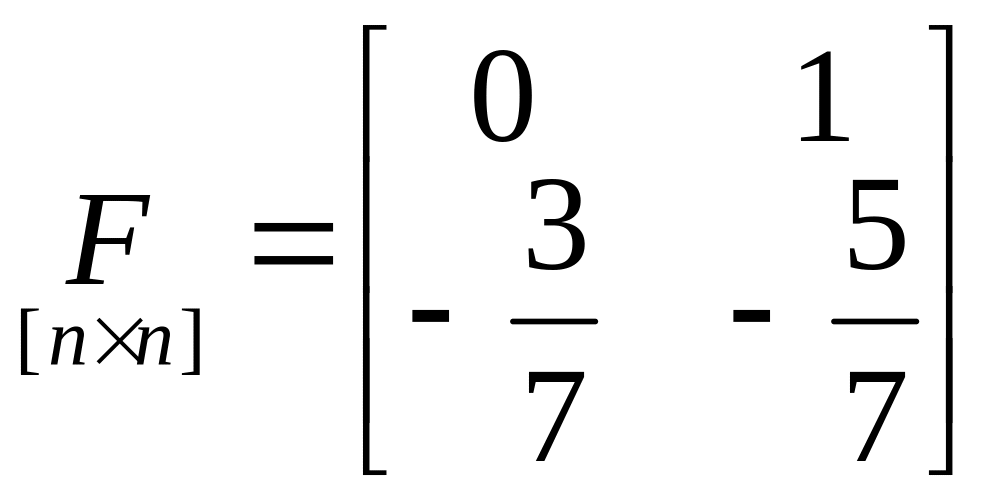Скалярное представление:
Пример
Описать, используя процедуру 1, систему уравнений в пространстве состояний, если задано дифференциальное уравнение 3-ого порядка связывающее вход/выход в виде:
Решение:
;
;
;
; 
;
; 
;
; 
.
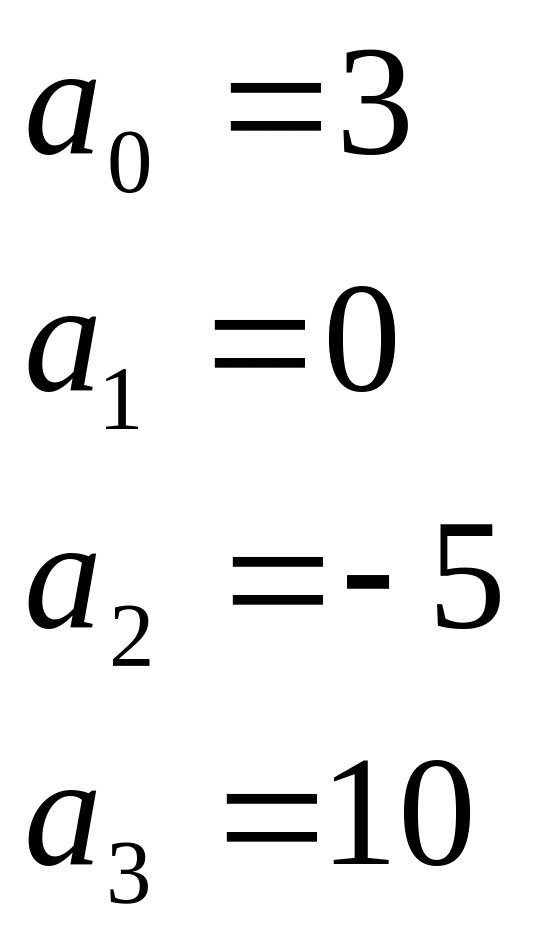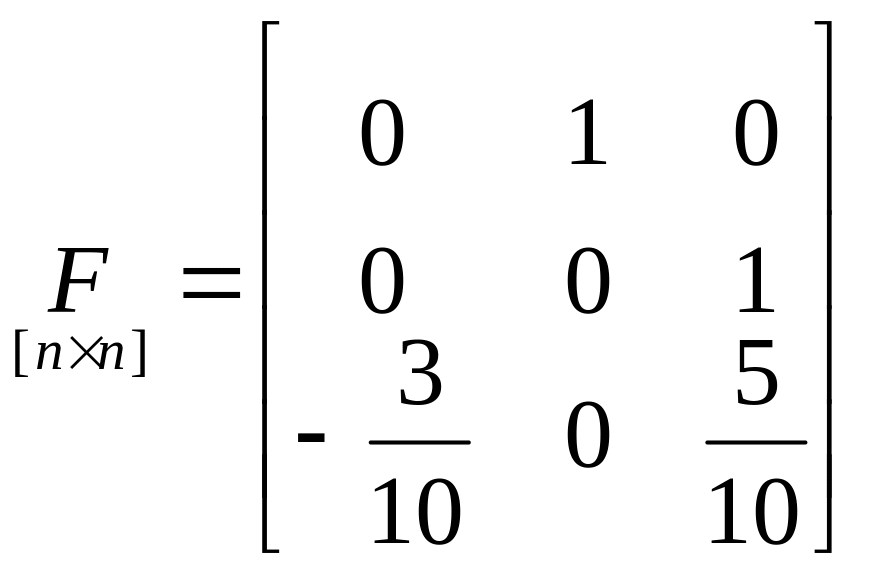Скалярное представление:
Процедура 2
(1 выход) (1 вход)
В процедуре 2 переменные вектора состояний являются линейной комбинацией производных входных и выходных переменных систем, т.е.:
При этой процедуре матрица является:
; 
;
;
.
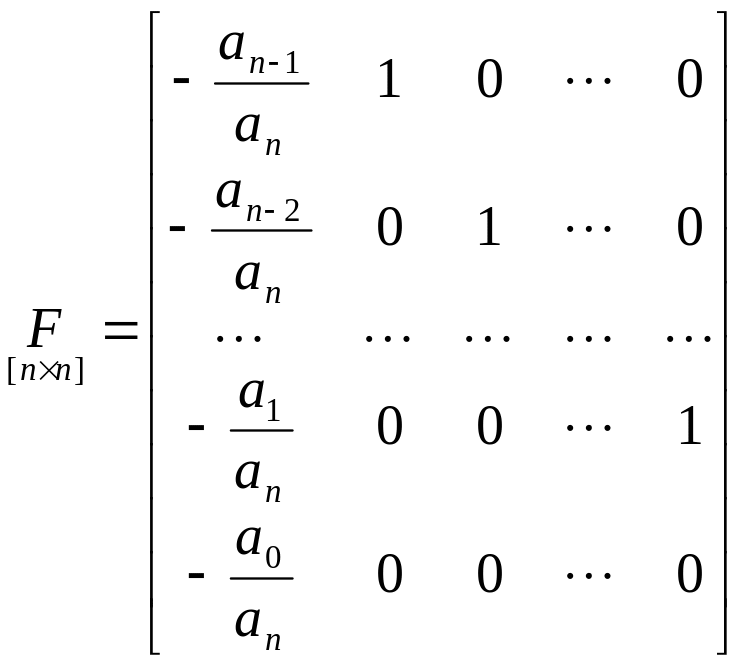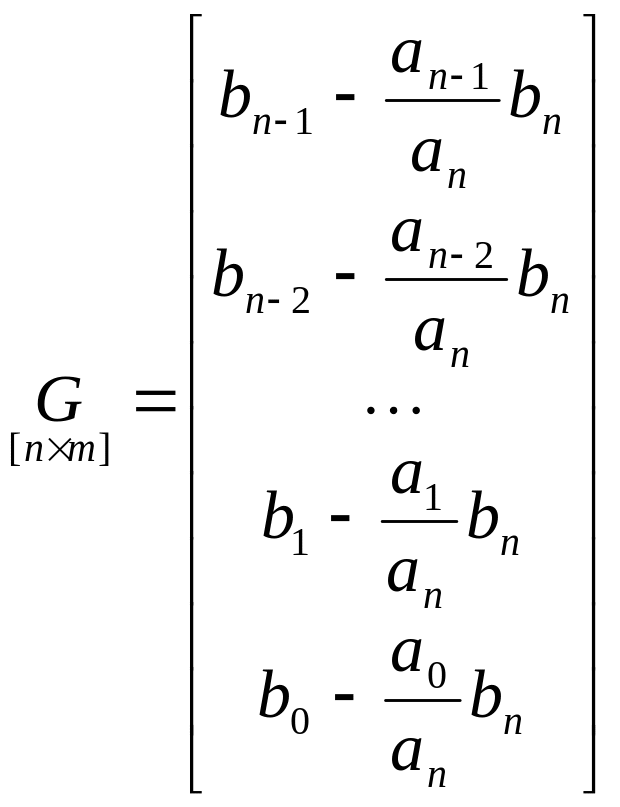При
и произвольном значении
от
в процедуре 2 управляемый процесс
есть компонента вектора состояний
.
Пример
Решение:
; ; ;
; ;
; 
;
;
.
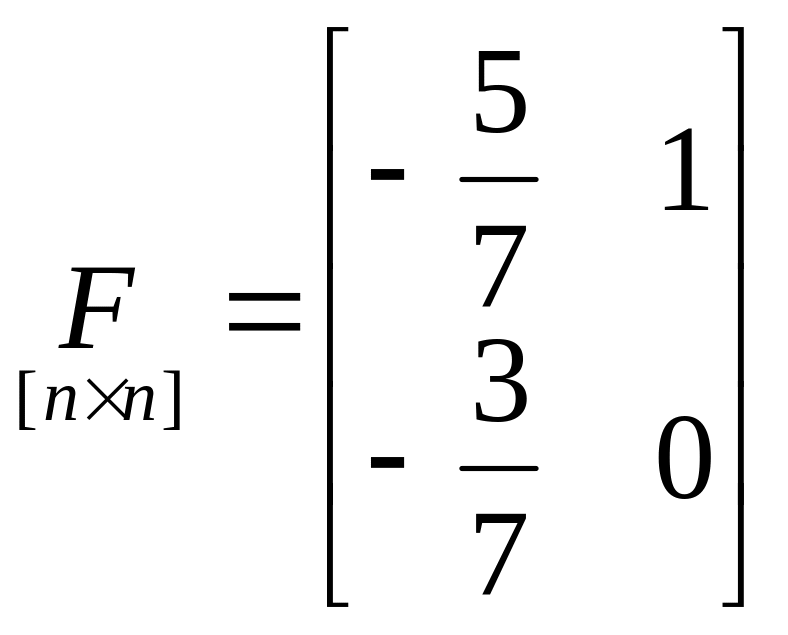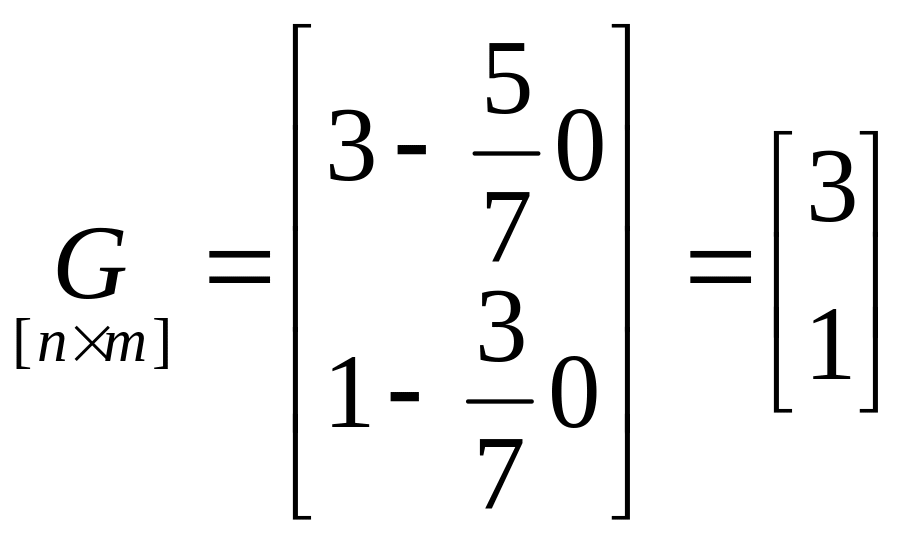Скалярное представление:
Пример
Решение:
; ; ;
; ;
; 
;
;
.
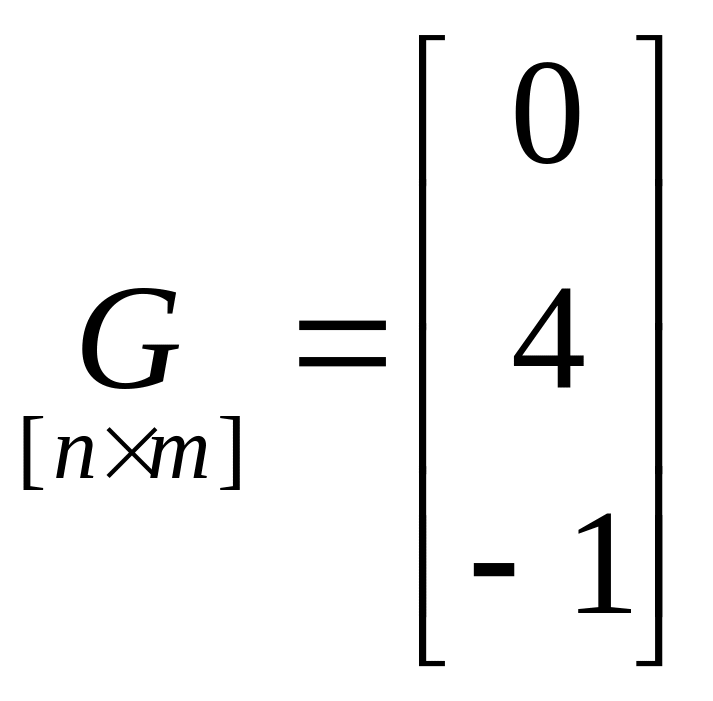Скалярное представление:
Процедура 3 (Разложение на элементарные дроби)
Дано:
Надо представить систему в пространстве состояний.
;
; степень
числителя
степени знаменателя
.
Характеристический многочлен:
;
,
где
– корни характеристического уравнения
;
;
– коэффициент разложения передаточной
функции на элементарные дроби:
при
.
;
Введем обозначение:
;
является изображением или
-образом
сигналов
представляющая собой реакцию устройства
с передаточной функцией
на входное воздействие
,
-образ
которого
.
Возьмем обратное преобразование Лапласа от обоих частей этого уравнения.
; 
;
;
В результате получим дифференциальных уравнений 1-го порядка в нормальной форме Коши и алгебраическое уравнение.
Полученная система есть модель этой системы в пространстве состояний, векторно-матричная форма которой определяет матрицу динамики :
; 
;
; 
.
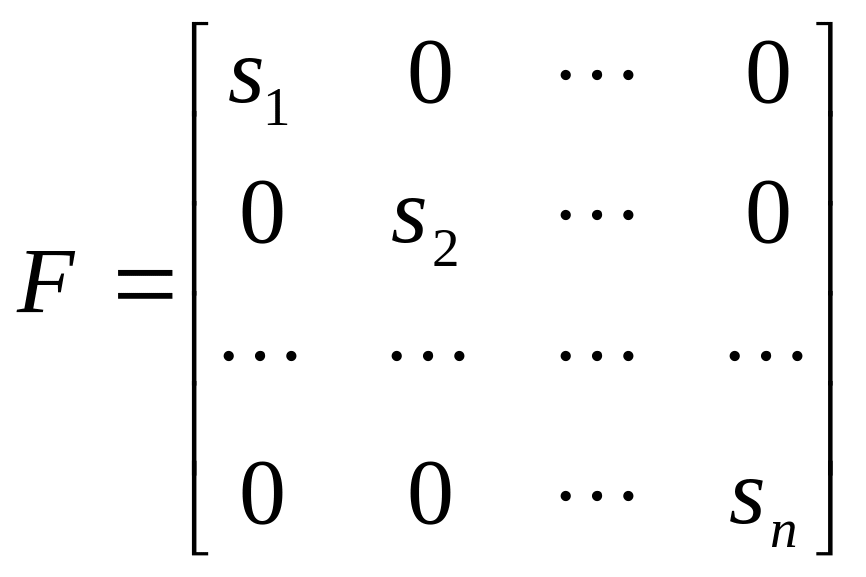Пример
.
Решение:
;
;
Найдем корни :
;
;
;
;
.
; 
;
; 
.
Пример
;
Решение:
;
Найдем корни :
;
;
;
;
.
;
;
;
.
Структурные схемы САУ по данным модели в пространстве состояний
Структурные схемы являются отображением тех математических моделей, которые используются для описания систем.
Одной и той же системе могут соответствовать различные модели и различные структурные схемы.
Пример
; 
;
; 
.
Решение:
.
Пример
;
;
;
.
Решение:
.
Переходная (фундаментальная) матрица системы
– переходная матрица системы.
Пусть система задана в векторно-матричной форме:
и пусть для всех компонентов системы и процессов протекающих в ней
;
;
;
.
Уравнения и в -образах:
;
;
;
;
;
Введем обозначение:
;
;
;
;
;
Пусть
– нулевые начальные условия
;
;
;
;
– матрично-передаточная функция,
задающая преобразования входных сигналов
в выходные сигналы
,
размерность которой
.
При
– скалярная передаточная функция. В
общем случае это матрица, элементы
которой задают преобразования
соответствующего входного сигнала в
соответствующий выходной сигнал.
;
;
;
– задает преобразования входных сигналов
в компоненты вектора состояния.
, где
;
– присоединенная матрица.
Если
,
то
,
где
– алгебраическое дополнение элемента
матрицы
.
Используя обратное преобразование Лапласа и теорему о свертке получим решение уравнения и относительно вектора состояния и управляемых процессов .
;
;
; –
матричная весовая функция.
;
.
Рассмотрим свободную составляющую
.
Матрица
показывает по какой траектории система
переходит из произвольного начального
условия
в точке 0 в конечное.
–
матричная экспонента.