Весовая функция системы



Если взять обратное преобразование Лапласа от левой и правой части , то

Используя свойство преобразования Лапласа определенное теоремой о свертке

; ,

получим:

, где 

– прообраз от передаточной функции – весовая функция;

;

.

называется весовой функцией преобразования вход-выход, поскольку с ее помощью взвешивается значение одной переменной в «прошлом» в моменты времени , для того, чтобы суммируясь определить значение реакции выхода в момент времени .

С помощью этой функции можно определить реакцию на любое входное воздействие.

Уравнение  позволяет определить реакцию выхода системы, если задан и вход и весовая функция .

Если известна передаточная функция, мы всегда можем найти весовую функцию.

Физический смысл весовой функции:

Переходная функция системы

Переходная функция – реакция системы на входное воздействие, которое называется функцией Хевисайда.

Функция Хевисайда представляет собой воздействие вида:

;

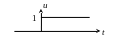
Переходная функция обозначается и может быть вычислена с помощью весовой функции.

Если , то

Используя преобразование Лапласа

,

получим

;

.

 и  – приводят к разрушению системы.

Описание структуры сау

Пусть система состоит из звеньев:

Уравнение связи для некоторого -ого звена будет иметь вид:

, где 

– коэффициент связи;

– непосредственный вход из внешней среды на это звено.

Используя передаточную функцию [стр. 11]:

; ;

;

; 

 ; 

Подставляя  в  получаем:

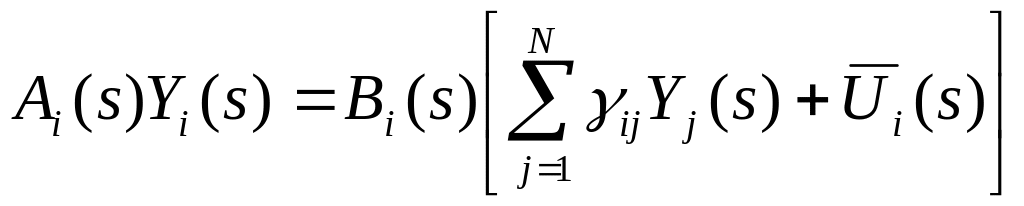
, где 

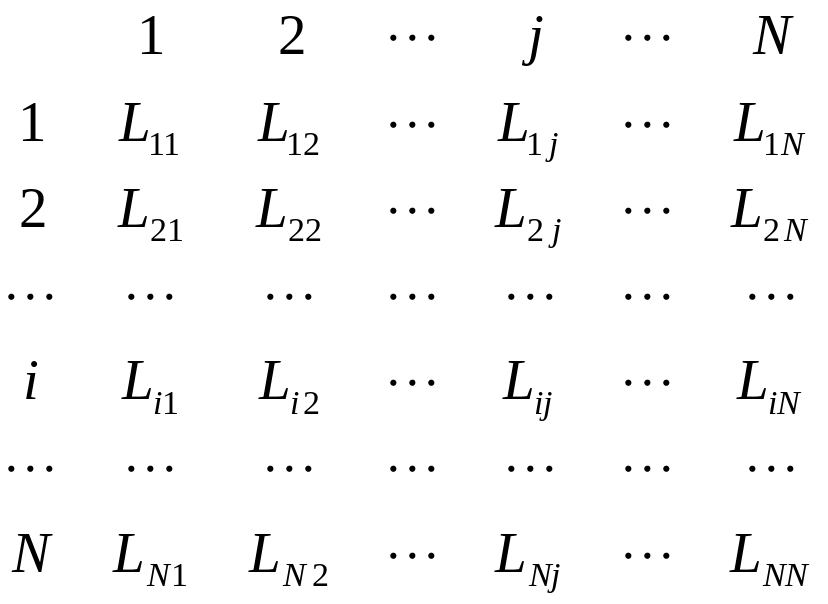
 – описание системы в терминах преобразования вход-выход, представленное системой линейных алгебраических уравнений. Коэффициенты при неизвестных , где и меняются от 1 до .

Правой частью являются внешние возмущения на систему.

Используя правило Крамера [стр. 83] запишем:

, где

– алгебраическое дополнение элемента ;

– определитель системы.

Обозначим

,

тогда

.

– передаточная функция, задающая характер преобразования -го входа по отношению к -му выходу системы.

Комплексная частотная характеристика сау

– является преобразованием Фурье от весовой функции :

;

Комплексная частотная характеристика является комплексной величиной.

Комплексная частотная характеристика как и передаточная функция есть отношение выходного гармонического сигнала к гармоническому сигналу на входе комплексном виде, принимающую множество значений в зависимости от частоты гармонического сигнала .

; .

Представление в полярных координатах:

, где

называется амплитудно-частотной характеристикой системы и представляет собой отношение амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе , при частоте входного сигнала равной , что означает, что если – некоторая амплитуда

, то

сигнал на выходе

зависит от частоты.

.

– фазо-частотная характеристика показывает на сколько выходной сигнал при заданной частоте сдвинут по фазе относительно входного сигнала .

– вещественная часть комплексной частотной характеристики системы;

– мнимая часть комплексной частотной характеристики системы.

и – полярные координаты частотной характеристики.

Между полярными координатами и , существует однозначное соответствие:

;

;

;

.

При каждом фиксированном значении частоты значение однозначно определяет точку на комплексной области … с декартовыми координатами и или полярными координатами и .

можно изобразить на комплексной области в виде годографа вектора в зависимости от частоты , где изменяется от до .

Часть годографа при от до симметрична части годографа при от до .

При экспериментальном определении комплексной частотной характеристики на вход системы подают гармонический сигнал , то выход системы будет меняться по закону , причем и при неизменной амплитуде будут зависеть от частоты .

Каждому фиксированному значению частоты будут соответствовать определенные значения и , а следовательно вычисленная для данной частоты

.